R-多元相关分析与回归分析

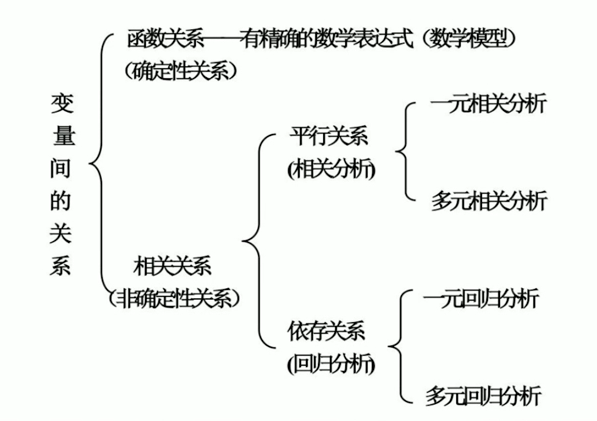
相关变量间的关系有两种：一种是平行关系，即两个或两个以上变量相互影响。另一种是依存关系，即是一个变量的变化受到另一个或多个变量的影响。相关分析是研究呈平行关系的相关变量之间的关系。而回归分析是研究呈依存关系的相关变量间的关系。 

步骤： 建立模型、求解参数、对模型进行检验

相关分析：通过计算变量间的相关系数来判断两个变量的相关程度及正负相关。

相关系数：两组不同数据的相关程度，取值范围在（-1，1），== 0不相关，>0时则两个变量为正相关，<0时则两个变量为负相关。

## 协方差相关系数
?cor()

## 相关系数假设检验
?cor.test()

## 
library(Hmisc)
library(corrplot)#先加载包
data(mtcars)
mydata <- mtcars[, c(1,3,4,5,6,7)]
head(mydata, 6)

## 一元相关性分析
res <- cor(mydata$mpg, mydata$disp)

##一元相关系数假设检验
cor.p = cor.test(mydata$mpg, mydata$disp)$p.value



##  多元相关性分析
ress <- cor(mydata)

##一元相关系数假设检验
ress.p <- rcorr(as.matrix(mydata))
## 查看显著性p-value
ress.p$P


### 可视化
corrplot(ress, type = "upper", order = "hclust", tl.col = "black", tl.srt = 45)
corrplot(ress.p$r, type="upper", order="hclust", p.mat = ress.p$P, sig.level = 0.01, insig = "blank")

回归分析通过研究变量的依存关系，将变量分为因变量和自变量，并确定自变量和因变量的具体关系方程式

建模

直线模型为：

y=a+bx

一个因变量与多个自变量间的线性数量关系可以用多元线性回归方程来表示：

y=b0+b1x+b2x ... +bnxn

曲线回归模型为：

二次函数

y=a+bx+cx^2

对数函数

y=a+blogx

指数函数

y = ae^bx或y = ae^(b/x)

幂函数

y=ax^b (a>0)

双曲线函数

y = a+b/x

求解回归系数

对回归系数方差分析检验、t检验

最终确定建立的数据模型： Y = a +bX ...

library(ggplot2)
library(Hmisc)
library(corrplot)
library(lmtest)
library(psych)

##1、 读取数据
data = read.table("ad_result.txt", header = T, sep = "t", row.names = 1)
head(data,4)

##2、探索数据，首先确认相关性：
##  计算其相关性系数并可视化
ress = cor(data)   ## 范围【-1, 1】 =0 不相关， > 0 正相关， < 0 负相关
ress.p <- rcorr(as.matrix(data))$P ## 相关性系数的检验 < 0.05 阈值 
corrplot(ress, type = "upper", order = "hclust", tl.col = "black", tl.srt = 45)  ## 相关系数矩阵可视化
pairs.panels(data)    ## 散点图矩阵 可视化



### 3、基于数据训练模型, 选择回归模型 （这里用lm() lm(formula = y ~ x1 + x2 + ...)）

fm.model = lm(install ~ tvcm + magazine, data)
as.data.frame(fm.model$coefficients)




## 4 、评估模型，对回归系数方差分析检验、t检验
anova(fm.model)

summary(fm.model)

#Residuals残差也就是预测值和实际值之差，我们将残差的分布用四分位数的方式表示出来，就可以据此来判断是否存在较大的偏差。

#Coefficients 这里是与预估的常数项和斜率相关的内容。每行内容都按照预估值、标准误差、t 值、p 值的顺序给出。我们可以由此得知各个属性的斜率是多少，以及是否具有统计学意义。

#Multiple R-squared、Adjusted R-squared 判定系数越接近于1，表示模型拟合得越好。


## 5、优化模型，用残差分析剔除异常点 检验异方差
plot(fm.model,which=1:4)
data.re = data[-c(1,2,10),]
fm.model1 =  lm(install ~ tvcm + magazine, data.re)
summary(fm.model1)
gq.p = gqtest(fm.model1)
bp.p = bptest(fm.model1)


## 如果gq.p || bp.p 小于0.05，需要进行修正异方差
lm.test2 = lm(log(resid(fm.model1)^2)~ tvcm + magazine,data.re)
lm.test3<-lm(install ~ tvcm + magazine,weights=1/exp(fitted(lm.test2)),data.re)
summary(lm.test3)



## 最后建立模型：
新用户数= 1.361× 电视广告费+ 7.250× 杂志广告费+ 188.174

参考R实战整理

library(psych)

height=c(65.1,68,69.1,70.2,71.8,73.7,77.9,80.1,84.2,86.8,88.8,92.5)
age=18:29
data = data.frame(age = age, height = height)
plot(age,height)

shapiro.test(height)
cor(data)
pairs.panels(data) 

fit.lm = lm(height ~ ., data)
summary(fit.lm)
data$height
fitted(fit.lm)
residuals(fit.lm)
plot(data$age, data$height)
abline(fit.lm)
dev.off()


fit.lm2 = lm(height ~ age + I(age^2), data)
summary(fit.lm2)


fit.lm3 = lm(height ~  I(age^2), data)
summary(fit.lm3)
anova(fit.lm2, fit.lm3)


######多元线性回归
library(psych)
data(state)
summary(state.x77)
state = as.data.frame(state.x77[,c("Frost", "Population", "Illiteracy", "Income", "Murder")])
pairs.panels(state)
state.fit = lm(Murder ~ Population + Frost + Illiteracy + Income, state )
summary(state.fit)

## 置信区间  置信区间若包含0，则考虑是否无效
confint(state.fit)
###############################################


## 回归诊断 标准方法
par(mfrow = c(2,2))
plot(state.fit)

## 改进的方法car 包
### 正态性 当预测变量值固定时，因变量成正态分布，则残差值也应该是一个均值为0的正态分布。n-p-1个自由度的t分布下的学生化残差
library(car)
state = as.data.frame(state.x77[,c("Frost", "Population", "Illiteracy", "Income", "Murder")])
state.fit = lm(Murder ~ Population + Frost + Illiteracy + Income, state )
qqPlot(state.fit)

state["Nevada",]
fitted(state.fit)["Nevada"]
residuals(state.fit)["Nevada"]


#### 误差的独立性 car包提供了一个可做Durbin-Watson检验的函数 如p值不显著（p=0.282）说明无自相关性，误差项之间独立。
d.pvalues = durbinWatsonTest(state.fit)
print(d.pvalues$p)


### 线性 若图形存在非线性，则说明你可能对预测变量的函数形式建模不够充分，
#那么就需要添加一些曲线成分，比如多项式项，或对一个或多个变量进行变换（如用log(X)代
#替X）
crPlots(state.fit)


### 检验同方差性 计分检验不显著（p=0.19），说明满足方差不变假设
ncvTest(state.fit)
spreadLevelPlot(state.fit)



### 多重共线性 
##暂无



####  异常观测值
## 一个全面的回归分析要覆盖对异常值的分析，包括离群点、高杠杆值点和强影响点。

### 离群点
##是指那些模型预测效果不佳的观测点。它们通常有很大的、或正或负的残差（Yi??? Y??i ）。正的残差说明模型低估了响应值，负的残差则说明高估了响应值。
##该函数只是根据单个最大（或正或负）残差值的显著性来判断是否有离群点。若不显著，则说明数据集中没有离群点；若显著，则你必须删除该离群点，然后再检验是否还有其他离群点存在。

library(car)
outlierTest(state.fit)


### 高杠杆值点 高杠杆值观测点，即是与其他预测变量有关的离群点。换句话说，它们是由许多异常的预测 变量值组合起来的，与响应变量值没有关系。



### 强影响点 强影响点，即对模型参数估计值影响有些比例失衡的点。例如，若移除模型的一个观测点时模型会发生巨大的改变，那么你就需要检测一下数据中是否存在强影响点了。
avPlots(state.fit, ask = F, onepage = T, id.method= "identify")


### influencePlot()你还可以将离群点、杠杆值和强影响点的信息整合到一幅图形中
#影响图。纵坐标超过+2或小于???2的州可被认为是离群点，水平轴超过0.2或0.3
#的州有高杠杆值（通常为预测值的组合）。圆圈大小与影响成比例，圆圈很大
#的点可能是对模型参数的估计造成的不成比例影响的强影响点

influencePlot(state.fit, id.method = "identify")

########################################

##### 改进措施
#有四种方法可以处理违背回归假设的问题：
#??? 删除观测点；
#??? 变量变换；
#??? 添加或删除变量；
#??? 使用其他回归方法。
 
##  变量变换
#当模型不符合正态性、线性或者同方差性假设时，一个或多个变量的变换通常可以改善或调整模型效果。变换多用Y λ 替代Y
powerTransform()
boxTidwell()
boxTidwell()

## 模型比较  AIC值越小的模型要优先选择，它说明模型用较少的参数获得了足够的拟合度。
anova()
AIC()

##### 逐步回归中，模型会一次添加或者删除一个变量，直到达到某个判停准则为止。例如， 向前逐步回归MASS包中的stepAIC()
library(MASS)
stepAIC(state.fit, direction= ""backward)



#### 全子集回归可用leaps包中的regsubsets()函数实现



##############################
### 有交互项的多元线性回归
data(mtcars)

data.mtcars = mtcars[c("wt", "hp", "mpg")]
pairs.panels(fit.mtcars)
#fit.lm = lm(mpg ~ wt + hp, data.mtcars)
fit.lm = lm(mpg ~ wt + hp + wt:hp, data.mtcars)
summary(fit.lm)

PS： 参考线上资料

https://blog.csdn.net/Cocaine_bai/article/details/80534313

https://blog.csdn.net/tMb8Z9Vdm66wH68VX1/article/details/79544739

理解汇总

最后

以上就是完美云朵为你收集整理的R-多元相关分析与回归分析的全部内容，希望文章能够帮你解决R-多元相关分析与回归分析所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。