任务详解：

这节课主要介绍了离散随机变量，连续随机变量，多维随机变量等知识点。
掌握目标：
1、掌握常用离散随机变量分布
2、掌握常用连续随机变量分布，分布函数与概率密度函数的意义
3、了解随机变量函数的分布的求法
4、掌握多元随机变量(离散和连续),以及边缘分布和条件分布

1.离散随机变量

常见的几种离散随机变量：

0-1分布

典型的就是丢硬币，只丢一次

伯努利实验，二项分布

是0-1分布的推广，也可以是丢硬币，但是丢n次，有k次朝上($C_n^k$相当于下面的$\left(\begin{array}{c}n\\ k\end{array}\right)$)的概率，有n-k次朝下。
P { X = k } = ( n k ) p k q n − k , k = 0 , 1 , 2 , ⋯   , n , p + q = 1 , p , q ≥ 0 P{X=k}=begin{pmatrix}n\k end{pmatrix}p^kq^{n-k},k=0,1,2,cdots,n,p+q=1,p,qgeq0 P{X=k}=(nk​)pkqn−k,k=0,1,2,⋯,n,p+q=1,p,q≥0
验证以上两种分布满足概率的3个条件
1.概率≥0
2.$P(S)=1$（所有可能性加起来为1）
3.满足可列可加

泊松分布

P { X = k } = λ k e − λ k ! , k = 0 , 1 , 2 , ⋯   , n P{X=k}=frac{lambda^ke^{-lambda}}{k!},k=0,1,2,cdots,n P{X=k}=k!λke−λ​,k=0,1,2,⋯,n
具有泊松分布的随机变量在实际应用中是很多的.例如，一本书一页中的印刷错误数、某地区在一天内邮递遗失的信件数、某一医院在一天内的急诊病人数、某一地区一个时间间隔内发生交通事故的次数、在一个时间间隔内某种放射性物质发出的、经过计数器的$\alpha$粒子数等都服从泊松分布.泊松分布也是概率论中的一种重要分布。

2.连续随机变量

分布函数：F(x)=P(X<=x)
$$P(x_1<X<=x_2)=F(x_2)-F(x_1)=P(X\le x_2)-P(X\le x_1)$$
说人话：x在x1和x2之间的概率等于x2的概率减去x1的概率
分布函数F(x)具有以下的基本性质：
1°F(x)是一个不减函数。
事实上，由（3.1）式对于任意实数$x_1,x_2(x_1<x_2)$，有
F ( x 2 ) − F ( x 1 ) = P { x 1 < X ≤ x 2 } ≥ 0 F(x_2)-F(x_1)=P{x_1<Xleq x_2}geq0 F(x2​)−F(x1​)=P{x1​<X≤x2​}≥0
2°$0\le F(x)\le 1$，且
事件不可能发生
$$F(-\infty )=\underset{x\to -\infty }{\lim }F(x)=0$$
事件必然发生
$$F(\infty )=\underset{x\to \infty }{\lim }F(x)=1$$
---------------------------------------------------------割你没商量1------------------------------------------------------
例2一个靶子是半径为2m的圆盘，设击中靶上任一同心圆盘上的点的概率与该圆盘的面积成正比，并设射击都能中靶，以X表示弹着点与圆心的距离。试求随机变量X的分布函数.
解若x<0，则{X≤x}=0是不可能事件，于是
F ( x ) = P { X ≤ x } = 0. F(x)=P{Xleq x}=0. F(x)=P{X≤x}=0.
若0≤x≤2，由题意， P { 0 ≤ X ≤ x } = k x 2 P{0≤X≤x}=kx^2 P{0≤X≤x}=kx2，k是某一常数，为了确定k的值，取x=2，有 P { 0 ≤ X ≤ 2 } = 2 2 k P{0≤X≤2}=2^2k P{0≤X≤2}=22k，但已知 P { 0 ≤ X ≤ 2 } = 1 P{0≤X≤2}=1 P{0≤X≤2}=1，故得k=1/4，即
P { 0 ≤ X ≤ x } = x 2 4 P{0≤X≤x}=frac{x^2}{4} P{0≤X≤x}=4x2​
于是
F ( x ) = P { X ≤ x } = P { X < 0 } + P { 0 ≤ X ≤ x } = x 2 4 F(x)=P{Xleq x}=P{X<0}+P{0≤X≤x}=frac{x^2}{4} F(x)=P{X≤x}=P{X<0}+P{0≤X≤x}=4x2​
若x≥2，由题意{X≤x}是必然事件，于是
F ( x ) = P { X ≤ x } = 1. F(x)=P{X≤x}=1. F(x)=P{X≤x}=1.
综合上述，即得X的分布函数为
$$F(x)=\{\begin{array}{c}0,x<0,\\ \frac{x^2}{4},0\le x<2,\\ 1,x\ge 2.\end{array}$$
---------------------------------------------------------割你没商量1------------------------------------------------------

概率密度

一般，如上例2中的随机变量那样，如果对于随机变量X的分布函数$F(x)$，存在非负函数$f(x)$，使对于任意实数x有
$$F(x)={\int }_{-\infty }^{x}f(t)dt$$
则称X为连续型随机变量，其中函数f(x)称为X的概率密度函数，简称概率密度。
f ( x ) = lim ⁡ Δ x → 0 + F ( x + Δ x ) − F ( x ) Δ x = lim ⁡ Δ x → 0 + P { x < X ≤ x + Δ x } Δ x f(x)=lim_{Delta xto 0^+}frac{F(x+Delta x)-F(x)}{Delta x}=lim_{Delta xto 0^+}frac{P{x<Xleq x+Delta x}}{Delta x} f(x)=Δx→0+lim​ΔxF(x+Δx)−F(x)​=Δx→0+lim​ΔxP{x<X≤x+Δx}​
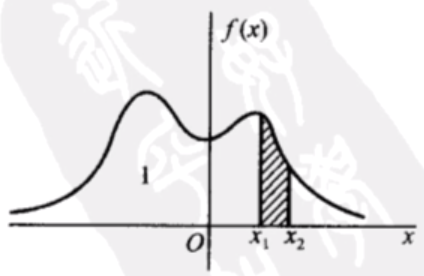
下图中$x_1,x_2$相当于$x,x+\Delta x$，概率密度相当于概率除以长度$\Delta x$，也就相当于当单位概率（单位长度上的概率）。

$f(x)$满足哪些性质？
1.$f(x)\ge 0$
2.$F(+\infty )={\int }_{-\infty }^{+\infty }f(t)dt=1$

常见的概率密度函数

（一）均匀分布

若连续型随机变量X具有概率密度
$$f(x)=\{\begin{array}{c}\frac{1}{b-a},a<x<b,\\ 0,其他.\end{array}$$
则称X在区间(a,b)上服从均匀分布.记为$X\sim U(a,b)$.

（二）指数分布

若连续型随机变量X的概率密度为
$$f(x)=\{\begin{array}{c}\frac{1}{\theta }{e}^{-x/\theta },x>0,\\ 0,其他.\end{array}$$
其中$\theta >0$为常数，则称X服从参数为$\theta$的指数分布。

（三）正态分布

若连续型随机变量X的概率密度为
$$f(x)=\frac{1}{\sqrt{2\pi }\sigma }{e}^{\frac{(x-\mu {)}^2}{2{\sigma }^2}},-\infty <x<+\infty$$
其中$\mu ,\sigma (\sigma >0)$为常数，则称X服从参数为$\mu ，\sigma$的正态分布或高斯（Gauss）分布，记为$XN(\mu ,{\sigma }^2)$。
引理：若$XN(\mu ,{\sigma }^2)$，则$Z=\frac{X-\mu }{\sigma }\sim N(0,1)$（标准正态分布）
---------------------------------------------------------割你没商量2------------------------------------------------------
例1设随机变量X具有以下的分布律，试求$Y=(X-1{)}^2$的分布律。

解：根据$Y=(X-1{)}^2$可知，Y的取值可以为：0,1，4

P { Y = 0 } = P { ( X − 1 ) 2 = 0 } = P { X = 1 } = 0.1 P{Y=0}=P{(X-1)^2=0}=P{X=1}=0.1 P{Y=0}=P{(X−1)2=0}=P{X=1}=0.1
P { Y = 1 } = P { X = 0 } + P { X = 2 } = 0.7 P{Y=1}=P{X=0}+P{X=2}=0.7 P{Y=1}=P{X=0}+P{X=2}=0.7
P { Y = 4 } = P { ( X − 1 ) 2 = 0 } = P { X = − 1 } = 0.2 P{Y=4}=P{(X-1)^2=0}=P{X=-1}=0.2 P{Y=4}=P{(X−1)2=0}=P{X=−1}=0.2
所以，Y的分布律为：

---------------------------------------------------------割你没商量2------------------------------------------------------
---------------------------------------------------------割你没商量3------------------------------------------------------
例2设随机变量X具有概率密度
$$f_X(x)=\{\begin{array}{c}\frac{x}{8},0<x<4,\\ 0,其他.\end{array}$$
求随机变量Y=2X+8的概率密度。
解思路是求概率密度，先要求分布函数。
已知X的概率密度函数：
$$X\to f_X(x)$$
求$Y=\phi (x)$的概率密度的套路：
$$F_Y(y)=P(Y\le y)$$
把Y的函数代入
$$=P(\phi (x)\le y)$$
转换为X的函数
$$=P(X\le {\phi }^{-1}(y))={\int }_{-\infty }^{{\phi }^{-1}(y)}{f}_X(x)dx$$
最后：
$$f_Y(y)=F_Y^{\prime }(y)=f_X({\phi }^{-1}(y))[{\phi }^{-1}(y){]}^{\prime }$$
---------------------------------------------------------割你没商量4------------------------------------------------------
来看看下面这个东西如何求出来的(注意这里的x与t没啥关系，主要是求x)：
$${\int }_{-\infty }^{\phi (x)}f(t)dt$$
用积分的定义，上面的式子可以写为：
$$=\underset{\Delta x\to 0}{\lim }\frac{{\int }_{-\infty }^{\phi (x+\Delta x)}f(t)dt-{\int }_{-\infty }^{\phi (x)}f(t)dt}{\Delta x}$$
$$=\frac{{\int }_{\phi (x)}^{\phi (x+\Delta x)}f(t)dt}{\Delta x}$$
根据中值定理${\int }_a^{b}f(x)dx=(b-a)f(\xi ),\xi \in (a,b)$：
$$=\underset{\Delta x\to 0}{\lim }\frac{(\phi (x+\Delta x)-\phi (x))f(\xi )}{\Delta x},\xi \in (\phi (x),\phi (x+\Delta x)$$

当$\Delta x\to 0时,有f(\xi )=f(\phi (x))$
$${\int }_{-\infty }^{\phi (x)}f(t)dt={\phi }^{\prime }(x)f(\phi (x))\text{\hspace{1em}(1)}$$
---------------------------------------------------------割你没商量4------------------------------------------------------

正式解题：
分别记X，Y的分布函数为$F_X(x)，F_Y(y)$.下面先来求$F_Y(y)$.
F Y ( y ) = P { Y ≤ y } = P { 2 X + 8 ≤ y } = P { X ≤ y − 8 2 } = F X ( y − 8 2 ) F_Y(y)=P{Yleq y}=P{2X+8leq y}=P{Xleq frac{y-8}{2}}=F_X(frac{y-8}{2}) FY​(y)=P{Y≤y}=P{2X+8≤y}=P{X≤2y−8​}=FX​(2y−8​)
将$F_Y(y)$关于y求导数，得Y=2X+8的概率密度为(用到公式1)
$$f_Y(y)=f_X(\frac{y-8}{2})(\frac{y-8}{2}{)}^{\prime }=\{\begin{array}{c}\frac{1}{8}(\frac{y-8}{2})\cdot \frac{1}{2},0<\frac{y-8}{2}<4,\\ 0,其他.\end{array}$$
$$=\{\begin{array}{c}\frac{y-8}{32},8<y<16,\\ 0,其他.\end{array}$$
---------------------------------------------------------割你没商量3------------------------------------------------------

3.多维随机变量(两个随机变量)

定义设(X,Y)是二维随机变量，对于任意实数x，y，二元函数：
F ( x , y ) = P { ( X ≤ x ) ∩ ( Y ≤ y ) } = = = 记 成 P { ( X ≤ x , Y ≤ y ) } F(x,y)=P{(Xleq x)cap(Yleq y)}overset{记成}{===}P{(Xleq x,Yleq y)} F(x,y)=P{(X≤x)∩(Y≤y)}===记成P{(X≤x,Y≤y)}
称为二维随机变量(X,Y)的分布函数，或称为随机变量X和Y的联合分布函数.

例1设随机变量X在1，2，3，4四个整数中等可能地取一个值，另一个随机变量Y在1~X中等可能地取一整数值.试求(X,Y)的分布律.
解由乘法公式容易求得(X,Y)的分布律.易知 { X = i , Y = j } {X=i,Y=j} {X=i,Y=j}的取值情况是：i=1，2，3，4，j取不大于i的正整数，且
P { X = i , Y = j } = P { Y = j ∣ X = i } P { X = i } = 1 i ⋅ 1 4 , i = 1 , 2 , 3 , 4 , j ≤ i P{X=i,Y=j}=P{Y=j|X=i}P{X=i}=frac{1}{i}cdotfrac{1}{4},i=1,2,3,4,jleq i P{X=i,Y=j}=P{Y=j∣X=i}P{X=i}=i1​⋅41​,i=1,2,3,4,j≤i
于是(X,Y)的分布律为

以上其实是联合分布函数$$F(x,y)=\sum _{x_i\le x}\sum _{y_i\le y}{p}_{ij}$$
该函数也要满足一下条件：
$$p_{ij}\ge 0,\sum _{i=1}^{\infty }\sum _{j=1}^{\infty }{p}_{ij}=1$$
用正规的语言来描述一下联合分布函数就是：
与一维随机变量相似，对于二维随机变量(X,Y)的分布函数F(x,y)，如果存在非负的函数f(x,y)使对于任意x，y有：
$$F(x,y)={\int }_{-\infty }^y{\int }_{-\infty }^{x}f(u,v)dudv$$
1°$f(x,y)\ge 0$
2°${\int }_{-\infty }^{+\infty }{\int }_{-\infty }^{+\infty }f(x,y)dxdy=F(-\infty ,+\infty )=1$
3°设G是xOy平面上的区域，点(X,Y)落在G内的概率为
P { ( X , Y ) ∈ G } = ∬ G f ( x , y ) d x d y P{(X,Y)in G}=iint_{G}f(x,y)dxdy P{(X,Y)∈G}=∬G​f(x,y)dxdy
4°若$f(x,y)$在点$(x,y)$连续，则有
$$\frac{{\partial }^{2}F(x,y)}{\partial x\partial y}=f(x,y)$$
之前的一维随机变量概率密度相当于概率除以长度$\Delta x$
二维随机变量概率密度则是概率除以面积，即随机变量x，y落在某单位面积上的概率。

边缘分布和条件分布

边缘分布

之前的 P { X = x i , Y = y j } P{X=x_i,Y=y_j} P{X=xi​,Y=yj​}是二维离散变量的联合概率分布形式，如果不关心Y，就对Y进行求和变成：
P { X = x i } = ∑ j = 1 ∞ P ( X = x i , Y = y j ) P{X=x_i}=sum_{j=1}^{infty}P(X=x_i,Y=y_j) P{X=xi​}=j=1∑∞​P(X=xi​,Y=yj​)
以上就是，X的边缘分布，这个只关心X，Y用求和的方式弄掉。
P { X = x i } = ∑ j = 1 ∞ p i j , i = 1 , 2 , ⋯ P{X=x_i}=sum_{j=1}^{infty}p_{ij},i=1,2,cdots P{X=xi​}=j=1∑∞​pij​,i=1,2,⋯
同理Y的边缘分布是：
P { Y = y j } = ∑ i = 1 ∞ p i j , j = 1 , 2 , ⋯ P{Y=y_j}=sum_{i=1}^{infty}p_{ij},j=1,2,cdots P{Y=yj​}=i=1∑∞​pij​,j=1,2,⋯
下面看连续变量，X的边缘分布就是把Y积分积掉：
$$f_X(x)={\int }_{-\infty }^{+\infty }f(x,y)dy$$
Y的边缘分布就是把X积分积掉：
$$f_Y(y)={\int }_{-\infty }^{+\infty }f(x,y)dx$$
---------------------------------------------------------割你没商量5------------------------------------------------------
引入边缘分布的主要是为了算条件概率，例如，知道联合分布$P(x,y)$，求y的条件下x发生的概率$P(x|y)$
$$P(x|y)=\frac{P(x,y)}{P(y)}$$
其中分母$P(y)$就是y的边缘分布，正规的讲法看下面：
---------------------------------------------------------割你没商量5------------------------------------------------------
P { X = x i ∣ Y = y j } = P { X = x i , Y = y j } P { Y = y j } = p i j p ⋅ j , i = 1 , 2 , ⋯ P{X=x_i|Y=y_j}=frac{P{X=x_i,Y=y_j}}{P{Y=y_j}}=frac{p_{ij}}{p_{cdot j}},i=1,2,cdots P{X=xi​∣Y=yj​}=P{Y=yj​}P{X=xi​,Y=yj​}​=p⋅j​pij​​,i=1,2,⋯
反过来：
P { Y = y j ∣ X = x i } = P { X = x i , Y = y j } P { X = x i } = p i j p i ⋅ , j = 1 , 2 , ⋯ P{Y=y_j|X=x_i}=frac{P{X=x_i,Y=y_j}}{P{X=x_i}}=frac{p_{ij}}{p_{icdot }},j=1,2,cdots P{Y=yj​∣X=xi​}=P{X=xi​}P{X=xi​,Y=yj​}​=pi⋅​pij​​,j=1,2,⋯
以上条件概率密度也是一种概率分布，也就满足概率分布的两个特性，一个是概率大于等于0，一个是求和等于1，数学描述就是：
1. P { X = x i ∣ Y = y j } ≥ 0 , P { Y = y j ∣ X = x i } ≥ 0 1.P{X=x_i|Y=y_j}geq0,P{Y=y_j|X=x_i}geq0 1.P{X=xi​∣Y=yj​}≥0,P{Y=yj​∣X=xi​}≥0
2. ∑ i = 1 ∞ P { X = x i ∣ Y = y j } = ∑ i = 1 ∞ p i j p ⋅ j = 1 p ⋅ j ∑ i = 1 ∞ p i j = p ⋅ j p ⋅ j = 1 2.sum_{i=1}^{infty}P{X=x_i|Y=y_j}=sum_{i=1}^{infty}frac{p_{ij}}{p_{cdot j}}=frac{1}{p_{cdot j}}sum_{i=1}^{infty}p_{ij}=frac{p_{cdot j}}{p_{cdot j}}=1 2.i=1∑∞​P{X=xi​∣Y=yj​}=i=1∑∞​p⋅j​pij​​=p⋅j​1​i=1∑∞​pij​=p⋅j​p⋅j​​=1
如果是连续的条件概率密度形式如下：
$$f_{X|Y}(x|y)=\frac{f(x,y)}{f_Y(y)}$$
也满足概率分布的两个特性，一个是概率大于等于0，一个是求和等于1。
简单证明第二个特性：
$${\int }_{-\infty }^{+\infty }{f}_{X|Y}(x|y)dx={\int }_{-\infty }^{+\infty }\frac{f(x,y)}{f_Y(y)}dx=\frac{1}{f_Y(y)}{\int }_{-\infty }^{+\infty }f(x,y)dx=1$$

独立性

连续型：$$f(x,y)=f_X(x)f_Y(y)$$
离散型： P { X = x i , Y = y j } = P { X = x i } P { Y = y j } P{X=x_i,Y=y_j}=P{X=x_i}P{Y=y_j} P{X=xi​,Y=yj​}=P{X=xi​}P{Y=yj​}

最后

以上就是娇气短靴为你收集整理的概率论：3.2随机变量与多维随机变量任务详解：1.离散随机变量2.连续随机变量3.多维随机变量(两个随机变量)边缘分布和条件分布的全部内容，希望文章能够帮你解决概率论：3.2随机变量与多维随机变量任务详解：1.离散随机变量2.连续随机变量3.多维随机变量(两个随机变量)边缘分布和条件分布所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。