牛老师考察の基础知识

一、奈奎斯特采样定理

定义：若连续信号x(t)是有限带宽的，其频谱的最高频率为fc。对x(t)抽样时，若保证抽样频率fs>2fc ，那么可由x(nTs)恢复出x(t)，即x(nTs)保留了x(t)的全部信息。

• 带宽：在某个频率范围内的信号频谱已经基本提供了我们需要的信息，那么这个频率范围外的信号频谱就变得可有可无。这个频率范围就是带宽。

若不能满足采样定理，则采样后信号的频率就会重叠，即高于采样频率一半的频率成分将被重建成低于采样频率一半的信号，这种频谱的重叠导致的失真称为混叠。

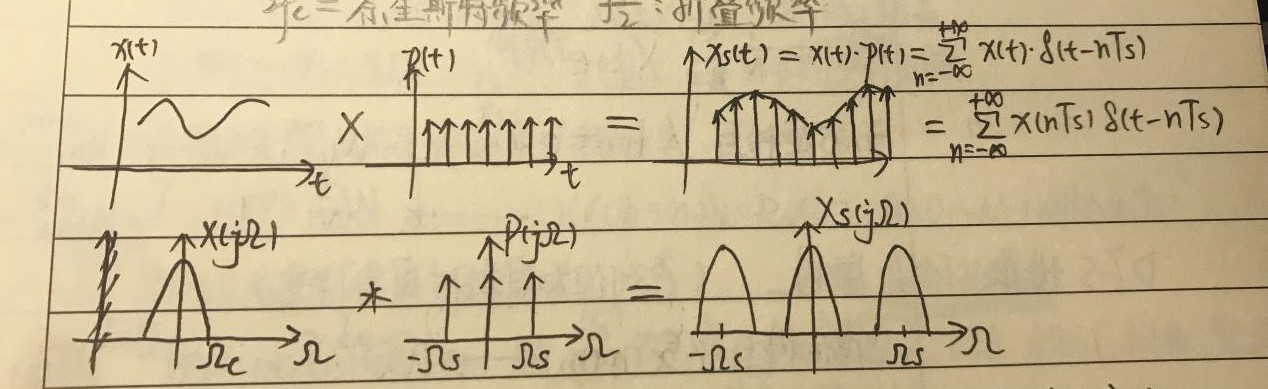
而实际存在的信号是有限长的，其频谱无限宽。因此，先将信号通过防混叠低通滤波器，再对x(t)进行抽样。抽样时，首先应了解x(t)的fc，再确定抽样频率fs，一般实际应用中保证采样频率为信号最高频率的2.56～4倍

采样信号的恢复：用低通滤波器从频谱中取出主频带，通过傅里叶反变换还原出信号。当同时满足（1）原信号为带限、（2）抽样频率大于两倍的最高频率、（3）抽样信号通过理想低通滤波器时，可从抽样信号不失真地恢复出原连续信号。而实际中，（1）（3）都无法满足，因此无法完全恢复出原信号。

二、有限/无限冲击响应系统

数字滤波器主要有无限冲击响应（Infinite Impulse Response，IIR）滤波器和有限冲击响应（Finite Impulse Response，FIR）滤波器。

二者区别为：

（1）IIR滤波器是指单位冲击响应长度为无限长的滤波器（系统不一定稳定），FIR滤波器是指单位冲击响应长度为有限长的滤波器（系统稳定）。

（2）IIR滤波器的单位冲击响应无限长，很难实现某种对称，即难实现线性相位。FIR滤波器的单位冲击响应有限长，容易实现某种对称，从而实现线性相位。

（3）IIR滤波器在有限Z平面内存在极点，而FIR滤波器在有限Z平面内不存在极点（对于因果系统，极点全部在z = 0处）。

（4）IIR滤波器采用递归型结构，带有反馈环路。FIR滤波器结构上主要是非递归结构，没有输出到输入的反馈。

三、滤波器

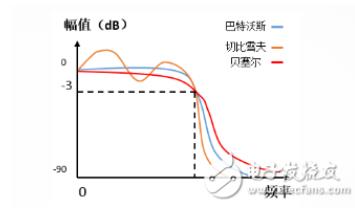
• 贝塞尔（Bessel）滤波器具有最平坦的幅度和相位响应，带通（通常为关注区域）的相位响应近乎呈线性。可用于减少所有IIR滤波器固有的非线性相位失真。

    常用于音频设备（在不损害频带内多信号的相位关系前提下，消除带外噪声），作为音频DAC输出端的平滑滤波器，或音频ADC输入端的抗混叠滤波器。

• 巴特沃斯滤波器（Butterworth filter）也被称作最大平坦滤波器。

其幅平方特性为 ，其中C为常数，N为阶次。由于滤波器的高通、带通、带阻设计可以在低通基础上完成，因此以下只讨论低通滤波器的情况。

滤波器特点是：

（1）通带内的频率响应曲线最大限度平坦，没有纹波，而在阻频带则逐渐单调下降为零。

（2）阶数N越大，幅频响应在截止频率处下降的越快。

（3）无论阶数如何变化，幅频响应曲线都保持同样的形状的滤波器。

（4）有较长的过渡带，在过渡带上很容易造成失真。

• 切比雪夫（Chebyshev）滤波器分为I型和II型，切比雪夫I型滤波器的振幅特性在通带内是等波纹的，在阻带内是单调的；切比雪夫II型滤波器在通带内是单调的，在阻带内是等波纹的。切比雪夫滤波器和理想滤波器的频率响应曲线之间的误差最小。
• 椭圆滤波器（Elliptic filter）是在通带和阻带等波纹的一种滤波器。它比切比雪夫方式更进一步地是同时用通带和阻带的起伏为代价来换取过渡带更为陡峭的特性。相较其他类型的滤波器，椭圆滤波器在阶数相同的条件下有着最小的通带和阻带波动。

相同阶数时：椭圆滤波器的幅频曲线下降最陡，其次为切比雪夫滤波器，再次为巴特沃斯滤波器，下降最平缓的为贝塞尔滤波器。

四、微积分基本定理（牛顿-莱布尼茨公式）

定义：一个连续函数在区间[ a，b ]上的定积分等于它的任意一个原函数在区间[a，b]上的增量。

五、特征向量与特征值

数学定义：设A是n阶方阵，如果存在常数λ及n维非零向量x，使得Ax = λx，则称λ是矩阵A的特征值，x是A属于特征值的特征向量。

意义：Ax是一个线性变换，这个变换把原来坐标系统变换到一个新的坐标系统X（由特征向量x组成）中。根据特征值排序，使得A投影的第一大方差在第一个坐标(称为第一主成分)上，第二大方差在第二个坐标(第二主成分)上，依次类推。

主成分分析经常选取特征值最高的k个特征向量表示一个矩阵，不仅对特征进行降维，而且保留方差贡献最大的特征。

六、高斯消元

高斯消元主要用来求解线性方程组，也可以求解矩阵的秩，矩阵的逆。

高斯消元的过程就是手算解方程组的过程，分两步：1. 加减消元 2. 回代求未知数值

解有三种情况：

（1）无解，消到最后发现有一行系数都为0，但常数项不为0

（2）多解，消到最后发现有好几行系数为0，常数项也为0（3）唯一解，除去前两种情况，即系数矩阵可以化成上三角阵。

七、中心极限定理&大数定理&泊松分布

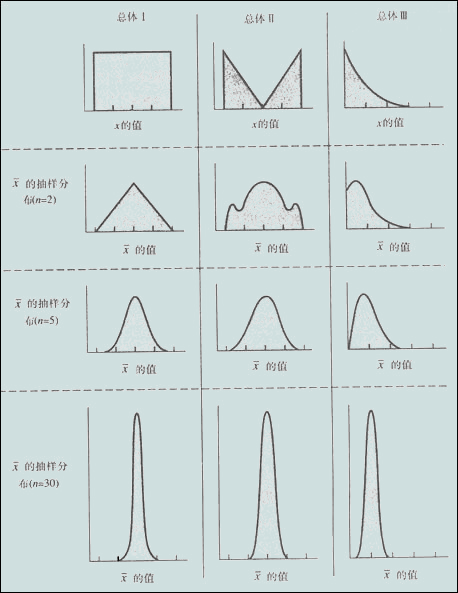
中心极限定理：当样本量n（并非样本大小）逐渐趋于无穷大时，n个抽样样本的均值的频数逐渐趋于正态分布，其对原总体的分布不做任何要求，意味着无论总体是什么分布，其抽样样本的均值的频数的分布都随着抽样数的增多而趋于正态分布。

若用样本来估计出总体的标准差，总体标准差：将原来的标准差公式从“除以n”改为“除以n-1”即可

大数定律是说，若样本量n越来越大，这n个独立同分布的样本均值（是一个随机变量）会依概率收敛于真值u，但样本均值的分布未知。

泊松分布是二项分布的极限分布（n很大，p很小），用于描述在单位时间、空间中稀有事件发生数。

最后

以上就是结实小鸽子为你收集整理的牛老师考察の基础知识的全部内容，希望文章能够帮你解决牛老师考察の基础知识所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。