[离散时间信号处理学习笔记] 12. 连续时间信号的离散时间处理以及离散时间信号的连续时间处理...连续时间信号与离散时间信号之间的关系连续时间信号的离散时间处理离散时间信号的连续时间处理

连续时间信号与离散时间信号之间的关系

下表为各符号的解释

Symbol	FT	DTFT	Info
$x_c(t)$	$X_c(jOmega)$	-	连续时间信号
$x[n]$	-	$X(e^{jomega})$	离散时间信号
$s(t)$	$S(jOmega)$	-	周期脉冲函数、即采样函数
$x_s(t)$	$X_s(jOmega)$	-	信号周期采样的数学表示
$Omega_N$	-	-	奈奎斯特频率，也就是带限信号的受限频率
$Omega_s$	-	-	采样频率
$T$	-	-	采样周期
$h_r(t)$	$H_r(jOmega)$	-	连续时间低通滤波器
$h[n]$	-	$H(e^{jomega})$	离散时间单位脉冲响应
$h_c(t)$	$H_c(jOmega)$		连续时间单位脉冲响应

 

C/D转换

从$x_c(t)$到$x[n]$是一个连续到离散的过程，该过程包括以下步骤：

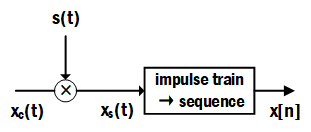
连续信号$x_c(t)$与采样信号$s(t)$相乘得到采样值加权的周期脉冲$x_s(t)$，最后再经过一步转换才能变成离散的采样序列$x[n]$，这就是一个数学上理想的连续到离散的转换，记为C/D。

 

D/C转换

那么反过来，从$x[n]$到$x_c(t)$就是一个离散到连续的过程，该过程包括以下步骤：

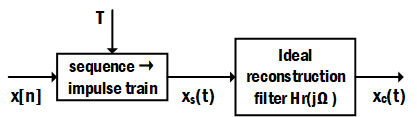
离散序列$x[n]$转换成周期为$T$的加权周期脉冲$x_s(t)$，然后就可以按照上一节课所描述的重构方法来得到原连续信号$x_c(t)$，这就是一个数学上理想的离散到连续的转换，记为$D/C$。

 

连续信号与离散信号的傅里叶变换之间的联系

离散时间序列$x[n]$与连续时间信号$x_c(t)$之间有如下关系

$x[n] = x_c(nT) , -infty<n<infty$

对$x_s(t)$进行傅里叶变换可以得到

$displaystyle{ X_s(jOmega) = sum_{n=-infty}^{infty}x_c(nT)e^{-jOmega T n} = sum_{n=-infty}^{infty}x[n]e^{-jOmega Tn} }$

对$x[n]$进行离散傅里叶变换可以得到

$displaystyle{ X(e^{jomega}) = sum_{n=-infty}^{infty}x[n]e^{-jomega n} }$

对比发现

$displaystyle{ X_s(jOmega) = X(e^{jomega})|_{omega = Omega T} = X(e^{jOmega T})}$

$X(jOmega)$相当于$X(e^{jomega})$进行了一个$omega = Omega T$的尺度变换，这是因为$x[n]$的离散时间傅里叶变换的是假设以$1$为周期对信号进行采集的，而这里实际的采集周期为$T$。

 

另外我们上一课通过傅里叶卷积定理得到了一个公式

$begin{align*}
X_s(jOmega) &= frac{1}{T}X_c*Ш_{frac{2pi}{T}}\
&= frac{1}{T}X_c(jOmega)*sum_{k=-infty}^{infty}deltaleft(Omega-frac{2pi k}{T}right)\
&= frac{1}{T}sum_{k=-infty}^{infty}X_cleft[jleft( Omega-frac{2pi k}{T} right )right ]quad delta convolution theorem\
&= frac{1}{T}sum_{k=-infty}^{infty}X_cleft( jleft(  Omega-kOmega_s right) right) quad letting Omega_s=frac{2pi}{T}
end{align*}$

结合上述结论，可以得到$x[n]$的DTFT为

$begin{align*}  X(e^{jomega})|_{omega=Omega T}
&= X(e^{jOmega T})\
&= X(jOmega) \
&= frac{1}{T}sum_{k=-infty}^{infty}X_cleft( jleft(  Omega-kOmega_s right) right) \
&= frac{1}{T}sum_{k=-infty}^{infty}X_cleft[ jleft(frac{omega}{T}-frac{2pi k}{T} right )right ] qquad left{begin{matrix}Omega &= &frac{omega}{T}\ Omega_s &= &frac{2pi}{T} end{matrix} right.\
end{align*}$

也就是说，如果对连续函数$x_c(t)$进行周期为$T$的采样得到离散序列$x[n]$，那么它们的傅里叶变换之间就有以下关系

$color{red}{begin{align*} X(e^{jomega})
&= frac{1}{T}sum_{k=-infty}^{infty}X_cleft[ jleft(Omega-frac{2pi k}{T} right ) right ]\
&= frac{1}{T}sum_{k=-infty}^{infty}X_cleft[ jleft(frac{omega}{T}-frac{2pi k}{T} right )right ] qquad omega=Omega T
end{align*}}$

 

 

连续时间信号的离散时间处理

在我们生活的世界当中，无论是声音、光、电等都是连续的信号，而计算机处理的是离散信号，因此一般来说我们都需要先把连续信号转换成离散信号，计算机对该离散信号进行处理后再重新转换为连续信号进行输出。

这里假设系统以及输入信号都满足奈奎斯特采样定理。接下来，我们主要讨论离散时间系统是如何对连续信号产生影响的。

频率响应

输出$y_r(t) = mathcal{F}^{-1}Y_{r}(jOmega)$，而通过对上图系统的逆推，我们可以得到以下式子

$begin{align*}
Y_r(jOmega)
&= H_r(jOmega)Y(e^{jomega}) qquad lowpass filter H_r(jOmega) for restruction\
&= H_r(jOmega)H(e^{jomega})X(e^{jomega})qquad LTI system frequency response H(e^{jomega})\
&= H_r(jOmega)H(e^{jOmega T})frac{1}{T}sum_{k=-infty}^{infty}X_cleft[jleft(Omega-frac{2pi k}{T} right )right ] \
&=left{ begin{matrix} H(e^{jOmega T})X_c(jOmega), & |Omega|<pi/T\ 0,& |Omega|geqslant pi/Tend{matrix}right.
qquad because H_r(jOmega) = left{begin{matrix}T, & |Omega|<pi/T\ 0, & |Omega|geqslant pi/T end{matrix}right.\
&= H_{eff}(jOmega)X_c(jOmega) qquad H_{eff}(jOmega) = left{ begin{matrix} H(e^{jOmega T}), & |Omega|<pi/T\ 0,& |Omega|geqslant pi/Tend{matrix}right.
end{align*}$

从该推导的式子可以得到以下结论

对于一个连续时间信号的离散时间处理系统，如果该系统满足两个因素：

• 离散时间系统的是LTI系统
• 输入信号为带限信号，并且采样率满足奈奎斯特采样定理

则该系统等效于一个连续时间LTI系统，其有效频率响应为

$color{red}{H_{eff}(jOmega) = left{ begin{matrix} H(e^{jOmega T}), & |Omega|<pi/T\ 0,& |Omega|geqslant pi/Tend{matrix}right.}$

 

单位脉冲响应

该等式可以说是指出了离散时间系统的频率响应$H(e^{jOmega T})$以及等效连续时间系统的频率响应$H_c(jOmega) = H_{eff}(jOmega)$之间的关系。那么它们的单位脉冲响应之间又具有怎样的关系呢？

这里假设连续时间单位脉冲响应$h_c(t)$与离散时间单位脉冲响应$h[n]$之间有如下关系

$h[n] = h_c(nT)$

那么有

begin{align*}
H_{eff}(jOmega) &= left{ begin{matrix} H(e^{jOmega T}), & |Omega|<pi/T\ 0,& |Omega|geqslant pi/Tend{matrix}right.\
&= left{ begin{matrix} displaystyle{frac{1}{T}sum_{k=-infty}^{infty}H_{c}left[jleft( Omega-frac{2pi k}{T} right)right]}, & |Omega|<pi/T\ 0,& |Omega|geqslant pi/Tend{matrix}right.qquad assume h[n]=h_c(nT)\
&= left{ begin{matrix} frac{H_c(jOmega)}{T}, & |Omega|<pi/T\ 0,& |Omega|geqslant pi/Tend{matrix}right.\
end{align*}

因此我们如果稍作调整，假设

$h[n] = Th_c(nT)$

则能使得$H_{eff}(jOmega) = H_c(jOmega),|Omega|<pi/T$。

 

 

离散时间信号的连续时间处理

这种系统相对来说较为罕见，一般不会用这种方法来实现离散时间系统，不过它提供了对某些离散时间系统的一种有用解释，如下面的例子，非整数延迟系统。

这里假设系统以及输入信号都满足奈奎斯特采样定理。因此有

$x_c(t) = displaystyle{ sum_{n=-infty}^{infty}x[n]frac{sin[pi(t-nT)/T]}{pi(t-nT)/T} }$

$y_c(t) = displaystyle{ sum_{n=-infty}^{infty}y[n]frac{sin[pi(t-nT)/T]}{pi(t-nT)/T} }$

式中，$x[n] = x_c(nT),y[n] = y_c(nT)$。它们在频域有如下关系（第一小节的结论）

$X_c(jOmega) = TX(e^{jOmega T}),qquad |Omega|<pi/T$

$Y_c(jOmega) = H_c(jOmega)X_c(jOmega)$

$Y(e^{jomega}) = frac{1}{T}Y_cleft( jfrac{omega}{T} right),qquad |omega|<pi$

这三条式子整理后可以得到

$color{red}{H(e^{jomega}) = H_c(jfrac{omega}{T}),qquad |omega|<pi}$

或者可以写成

$color{red}{H(e^{jOmega T}) = H_c(jOmega),qquad |Omega|<pi/T}$

 

例子

考虑一个离散时间系统，其频率响应为

$H(e^{jomega}) = e^{-jomegaDelta}$

当$Delta$是一个整数时，该系统有一个明确的解释——延迟$Delta$，即

$y[n] = x[n-Delta]$

当$Delta$不是整数时，上面的式子没有正规意义，也无法通过对$x[n]$移位得到输出。此时我们可以用本节学习的内容来进行解释，把该离散时间系统等效为对$x[n]$进行D/C转换后，进行连续时间处理，然后进行C/D转换得到输出。其中的连续时间处理系统的频率响应为

$H_c(jOmega) = H(e^{jOmega T}) = e^{-jOmega TDelta}$

通过该频率响应可以求得，对于连续时间信号$x_c(t)$以及连续时间信号$y_c(t)$，他们具有如下关系

$y_c(t) = x_c(t-TDelta)$

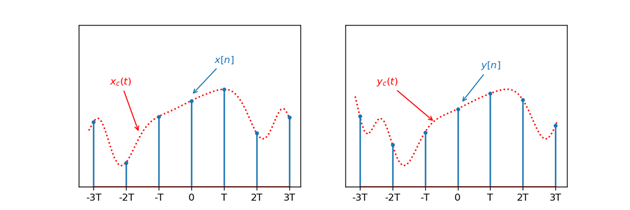
其中$x_c(t)$是通过对$x[n]$进行内插得到的，在对$x_c(t)$进行$TDelta$的延迟后得到$y_c(t)$，然后进行周期为$T$的采样则得到$y[n]$，即

$begin{align*}
y[n] &=y_c(nT)\
&= x_c(nT-TDelta)\
&= left.sum_{k=-infty}^{infty}x[k]frac{sin[pi(t-TDelta-kT)/T]}{pi(t-TDelta-kT)/T}right|_{t=nT}\
&= sum_{k=-infty}^{infty}x[k]frac{sinpi(n-k-Delta)}{pi(n-k-Delta)}qquad
end{align*}$

按照卷积的定义，该离散时间系统的单位脉冲响应为

$h[n] = frac{sinpi(n-Delta)}{pi(n-Delta)}$