（三）5.自动控制原理 Time domain analysis and correct 稳态误差

开始文章之前，我们需要注意一点

稳定的系统才有稳态误差可言，所以我们去求稳态误差的第一件事就是确保系统是稳定的

有差无差系统以及稳态误差的概述

无差系统：在单位阶跃的输入条件下，如果没有原理性误差，则为无差系统
有差系统：在单位阶跃的输入条件下，如果有原理性误差，则为有差系统

有差无差强调是在单位阶跃的条件下，因为输入变了可能误差也就变了

我们这里说的稳态误差只考虑原理性误差，不考虑非线性因素引起的误差

误差的两种定义方式

1.输入定义 ：在输入和反馈的汇入点后得到的是误差
2.输出定义：比较点后移到反馈传递函数后面得到

详细见下图，我们一般都是输入定义的稳态误差

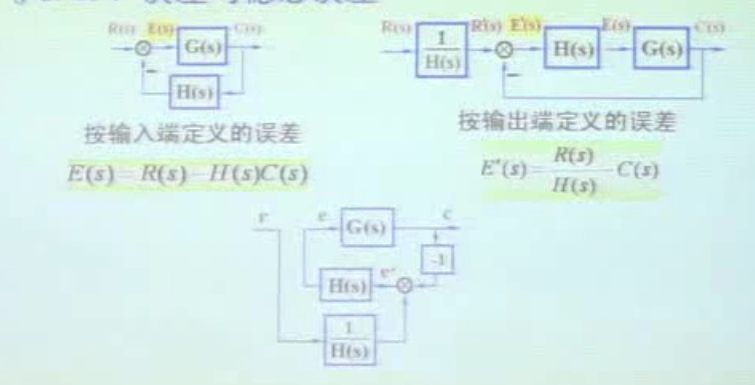
输入定义的稳态误差，就是R(S)-H(S)*C(S)，很容易理解，输入减去反馈

稳态误差的两种定义以及解体步骤

稳态误差 
1.ess = lim(t->∞) e(t)   这是常用的定义方式   静态误差
2.ess = e(t) 中的稳态分量， 动态误差

下面会先说静态误差，再说动态。

一般解法

步骤：

1.判断系统稳定性，确定稳定后再计算（一般问你稳态误差都是稳定的了，不需要疑神疑鬼）
2.求误差传递函数 φr 和  φn  （即输入-误差的传递函数和  扰动-误差的传递函数）
3.利用终值定理解出答案  ess = lim(s->0){ φr( s ) R ( s ) + φn ( s ) N ( s )} 

注意点：
1.求误差传递函数一定要注意：
        从输入（扰动） 到误差（输入定义，即输入和反馈的比较点后的输出为误差）
        才是这个结构图的前向通道，我们需要重构结构图
     比如下面这道题，E(s)/R(s) 的结构图实际上应该是  ：

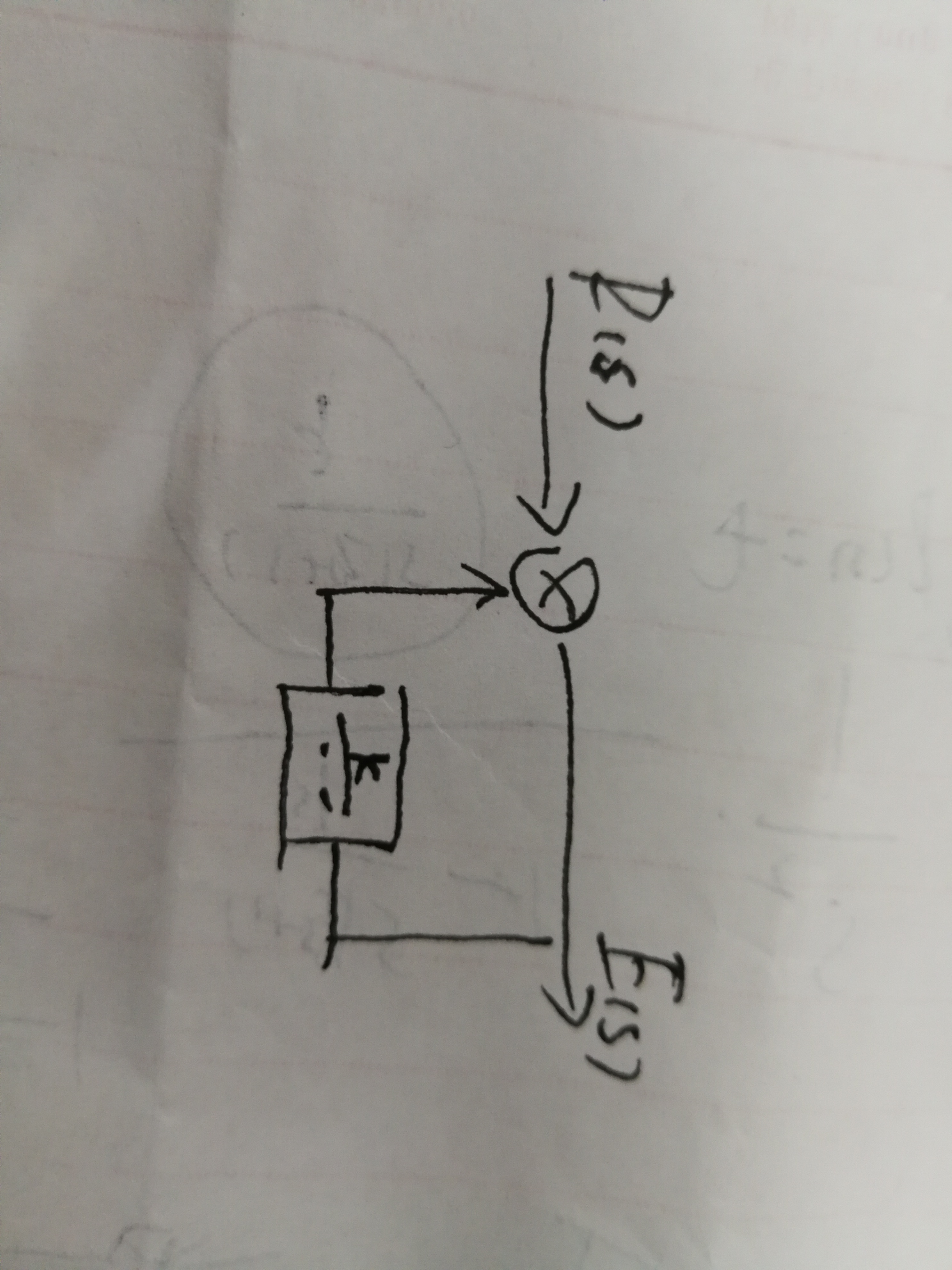
这样应该就可以理解了吧，再比如从扰动到误差：

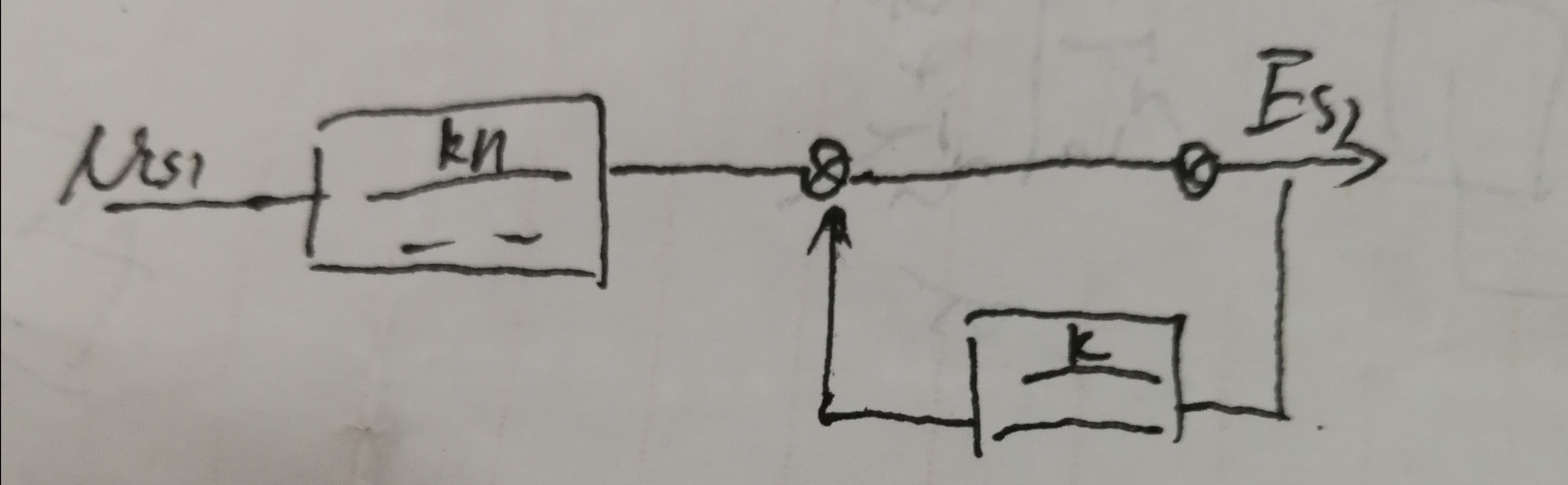
把结构图变形成为这样，相信大家就可以利用Mason公式很轻松解出误差传递函数了

看看题目真容

按照我们上面说的步骤，求出误差传递函数，终值定理解出相应部分的稳态误差，最后相加

从答案可以看出，稳态误差值与自身结构参数和反馈结构类型有关

上面说的必须是单位脉冲是对于有差无差而言，这里的则输入信号可随意，就像
这个题是斜坡相应一样

静态误差系数法

这个方法讨论不同输入的稳态误差情况

使用条件：

1.稳定系统
2.采用输入定义的误差
3.不能有前馈通道

先说几个概念

1.开环传递函数（没啥好说的）
2.系统型别v：观察开环传递函数的分母，说的文艺一点就是纯积分环节的个数，也就是在乘积模式下
单独的s^n为一项时候的n，事实上，目的就是希望吧这个s^n提出去之后的式子在s->0的时候等于1

注意！必须是在开环情况下去计算

针对一般情况，给出在不同形式的输入（阶跃/斜坡/二分之一平方）时候的稳态误差

上面是推导过程，下面罗列成表格

我们计算只需要按照公式去计算就可以了，先算静态误差函数，再算稳态误差

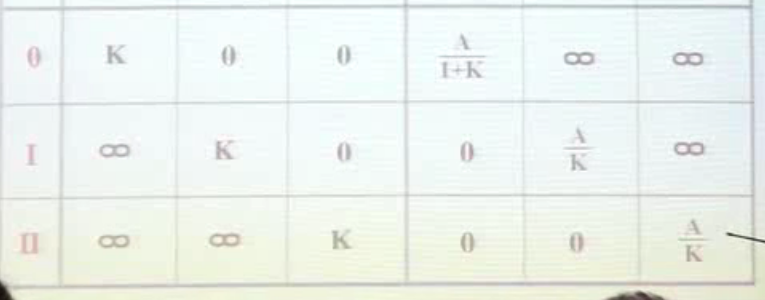
图有点模糊，给个高清

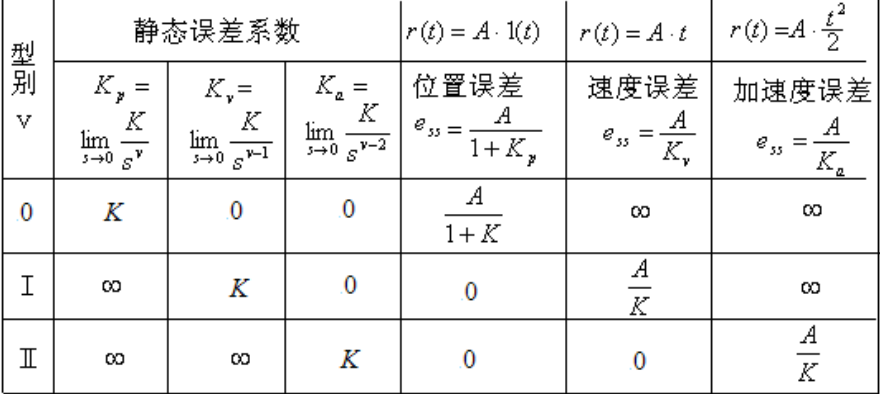
四个规律

1.型别相同时，系统的稳态误差是随着输入信号的档次的增加而增加（档次高就是t和分母上s的次方都变高，）
  eg. 档次从低到高==》u(t)----tu(t)-----1/2  u(t)/(t^2)
  档次相同时，稳态误差随着型别变大而变小
2.档次和型别对等的时候稳态误差是常数
3.档次高于型别，稳态误差  = ∞
4.档次低于型别，稳态误差 = 0

使用的时候注意点

1.计算出开环增益 k 和 型别 v（表格中的公式要用，有其实k，一定要算好了，尾一
								v的得出需要验证，是否提出去之后剩下的在s=0时，式子=1）
2.复合输入，则使用叠加原理

静态误差法只能用在标准型的结构图上，如果是畸形图，那可以借助表格进行分析，但是不能直接使用去和往常一样去算误差

给个例题
这个题目对新手来说肯定是拿到就静态误差法
但是必须要注意判断稳定性得到的范围啊啊啊啊啊！！！记得判稳！！！！

另外一个例题，做法不难，主要是结论了解一下

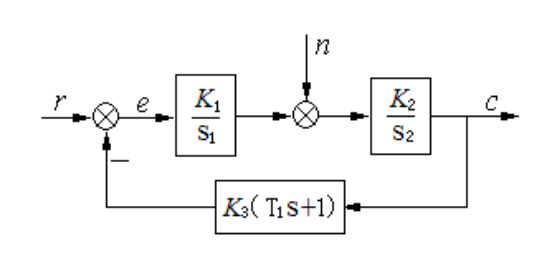
对这样一个结构图，想要改变干扰信号引起的误差，需要在干扰之前那个地方增大增益，或者加入积分环节，只有这里才会对干扰引起额误差产生影响

en = -A/k1 ess = A/k1k2k3

动态误差系数法

前面讲的静态误差，只能求出误差的稳态值，而我们现在说说动态误差，他可以帮助我们了解一个误差的稳态部分的变化之类的

思路

1.误差函数展开成泰勒级数
2.泰勒级数×输入得到误差
3.误差反变换

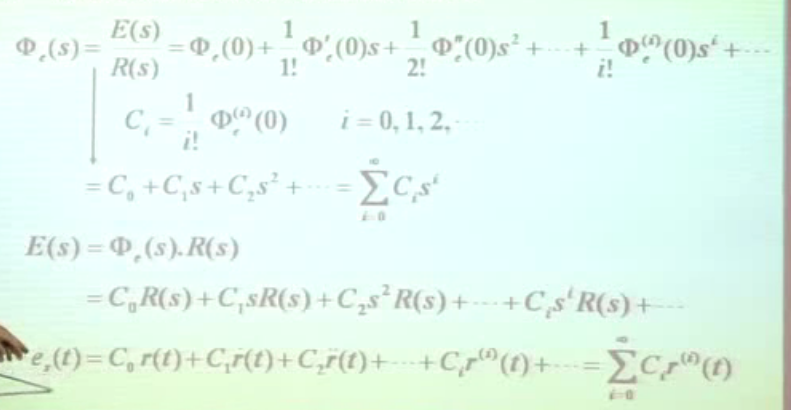
泰勒级数：难点和关键
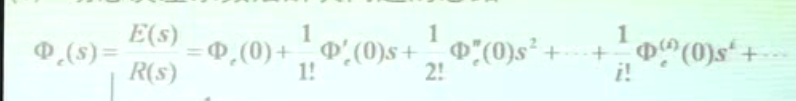方法：1.系数比较法，
2.长除法

我的考纲上没有，等以后有空了再写动态的吧

最后

以上就是尊敬钢笔为你收集整理的（三）5.自动控制原理 Time domain analysis and correct 稳态误差的全部内容，希望文章能够帮你解决（三）5.自动控制原理 Time domain analysis and correct 稳态误差所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。