简单典型二阶系统_自动控制原理要点---第二章 系统建模

1、建模方法：

实验法：人为给系统施加某种测试信号，记录相应的输出，然后用适当的数学模型去逼近，也称为系统辨识方法；
解析法：利用已有的物理规律和化学规律来分析系统各部分的运动机理，获取其运动方程。

2、常用的数学模型：

①时域中常使用的数学模型：微分方程、差分方程；
②复域中常用的数学模型：传递函数、结构图；
③频域中常用的数学模型：频率特性。

2.1、微分方程：通常，解析法对系统或元部件建模如下：

①分析系统运动的因果关系，确定其输入、输出、中间变量及其之间关系；
②从输入端开始，按照信号的传递顺序，依据各变量所遵循的物理（或化学）规律，列写出各个元部件的动态方程；
③消去中间变量，写出输入与输出变量的微分方程。

注：系统的数学模型越精确，微分方程的阶次越高，直接对高阶微分方程求解困难。
如果系统参数或者结构发生变化，需要重新建模并求解微分方程，不利于系统的分析与设计。

2.2、传递函数：在零初始条件下，输出信号c(t)的拉氏变换C(s)与输入信号r(t)的拉氏变换R(s)之比，记为G(s)：G(s)=

=

。

注：“零初始条件”有两个含义：
①指输入在t=0之后才作用于系统，因此t≤0时系统输入量及其各阶导数为0；
②输入作用于系统之前，系统是相对静止的，就是系统的输出量及其各阶导数在t≤0时也为0。

• G(s)的常用形式：

①有理分式形式

，式中

；

②零极点形式

，式中

为零点，

为极点，

为增益；

③时间常数形式

，

为时间常数，

为放大系数。

• 由G(s)时间常数形式可知，任一复杂系统的G(s)可由如下6个典型环节组成：

①比例环节：G(s)=

=K；

②惯性环节：G(s)=

=

；（因储能元件，输出量不能立即跟上输入信号）

③积分环节（也称无差环节）：G(s)=

=

(一阶)，

(二阶)；

④微分环节： G(s)=

=s(理想微分环节)，

(一阶)，

(二阶)；

⑤振荡环节：G(s)=

=

，式中

称为无阻尼振荡频率，

为阻尼比；

⑥滞后环节（也称延迟环节）： G(s)=

。

注：i.因为实际物理系统总是存在惯性，并且能源功率有限，使得传递函数的分母阶次n总是
大于或等于分子阶次m；
ii.传递函数只取决于系统的结构和参数，与外界作用无关；
iii.传递函数的拉氏反变换是系统的脉冲响应，即G(s)=C(s)/R(s)=C(s)（因为r(t)=δ(t)的拉氏变
换为R(s)=1）。

2.3、结构图 如下图，R(s)为指定输入信号，N(s)为干扰信号，C(s)为输出信号，E(s)为误差信号，其中R(s)与N(s)为系统的两个输入，E(s)和C(s)为系统的两个输出。

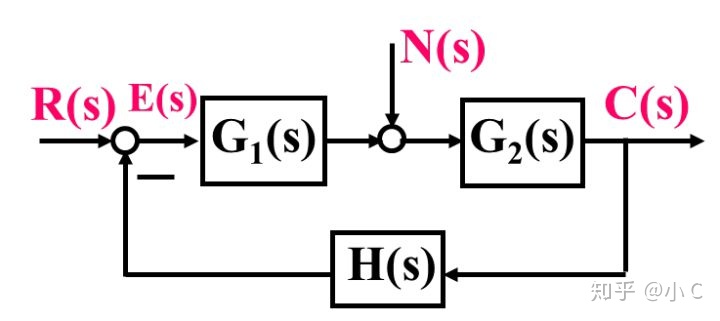
• 系统的开环传递函数：系统的主反馈信号B(s)与偏差信号E(s)之比，即

注：这里的开环传递函数是指闭环控制系统里的某一处开环的传递函数，而不是指开环控制
系统的传递函数。

• 系统的闭环传递函数

①当N(s)=0时，输出C(s)对给定输入R(s)的传递函数为

②当R(s)=0时，输出C(s)对扰动N(s)的传递函数为

当给定输入和扰动同时作用被控系统时，根据线性叠加原理，有

• 系统的误差传递函数

①当N(s)＝0时，则误差E(s)对R(s)的传递函数为

②当R(s)=0时，则误差E(s)对N(s)的传递函数为（简称扰动误差传递函数）

当给定输入和扰动同时作用被控系统时，根据线性叠加原理，系统误差为

注：当系统参数、结构发生变化时，微分方程形式模型需要重新建模，而传递函数形式模型
不必重新建模，这是因为经过拉普拉斯变换后串联、并联、反馈连接形式的环节，其运算变
为乘、加等低级运算，不再是微分运算。

2.4、频率特性：稳定的线性定常系统在正弦信号的作用下，系统输出的稳态分量与输入的复数之比；其中，输出的稳态分量振幅与输入的振幅比A(w)称为幅频特性，输出的稳态分量相位与输入的相角之差φ(w)称为相频特性，即

。

注：i.频率特性表征了系统或元件对不同频率正弦输入的响应特性；
ii.φ(ω)大于零时称相角超前，小于零时称相角滞后；
iii.频率特性反映了系统的内在性质,与外界因素无关。

3、数学模型是等价变换的：微分方程、传递函数、结构图、频率特性之间一一对应的。

欢迎大家前来交流相关自动控制问题。如有不对的地方，望不吝赐教！

***以上内容未经本人同意，禁止转载***