控制57闭环丝杠程序_理解数字控制系统的环路设计 入门级

前言：
  此文本人是菜鸡啄米，是自己工作的领悟，并且加入一些参考文档的内容。如果有错误之处，恳请指正，感激不尽。谢谢。

  从以往的模拟控制的经验过渡到数字系统，最易于理解的环路设计方法就是：通过平均小信号方法建模得到控制-输出传递函数，或者通过仿真获得。根据功率级的传递函数的频率响应和所需的系统闭环带宽，相位余量，等一系列动态性能的要求，来设计闭环控制器的传递函数。在模拟控制中，是根据闭环控制器的传递函数中的零极点分布，来选择运算放大器反馈上的电阻电容。易于理解这种方法在数字系统中的操作，就是将闭环控制器的传递函数根据控制器的调用(计算频率Ts)，通过双线性或替他方法离散的Z域。根据离散后获得的Z域差分方程系数，写成2P2Z，3P3Z或PID的控制系数，从而实现闭环控制。先不讨论这种方法的准确性与否，这个方法确实最易于被理解的一个思路，更符合我们的工程直觉。下图就是将控制器从s域离散到z域后，提取差分方程系数，得到B0,B1,B2,A1,A2参数。

  在数字控制系统中，为了最优化性能一般都是采用“单周期计算方式“。也就是在PWM开始发波后，触发ADC进行转换，然而等待ADC转换结束。产生EOC中断调用闭环控制程序，控制器在中断中计算完毕后。将PWM更新值写入到寄存器中，PWM模块再等待周期结束后载入新的PWM控制值，在新的开关周期中发波。下图展示了在周期的50%处触发ADC并启动控制的事件流程，在这种操作方法下。PWM的输出值与控制器输出值之间，永远都是延迟了一个开关周期。如果是2个开关周期调用一次闭环控制器，更新一次占空比值的话，控制器的输出值到实际开关管上就是延迟了两个开关周期。

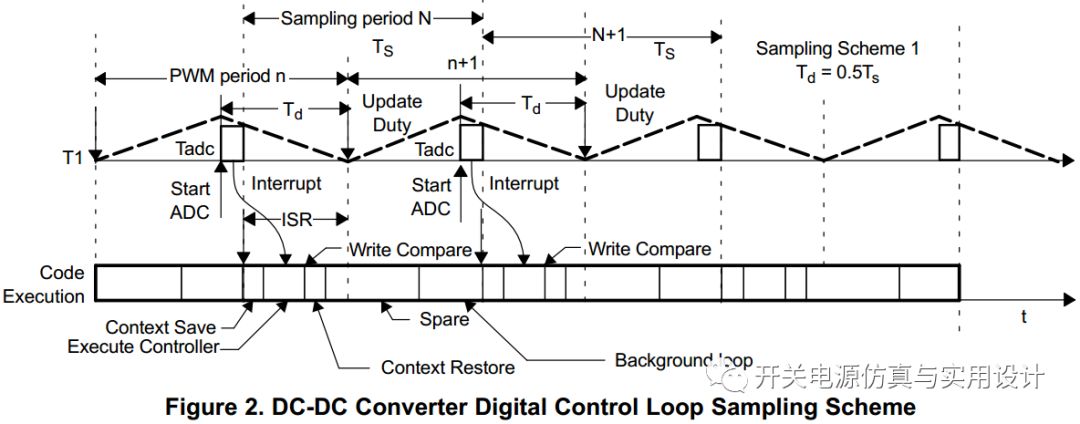
 上文提及了数字控制的基本方法，现在还需看看整个控制环路之中存在的其他环节。在上文中，我们为了简化分析，只考虑的功率级小信号模型，忽略了PWM增益和采样的问题。这里先讲采样的问题，在模拟控制中，我们通过把输出信号缩小到2.5V与系统闭环参考值进行减小计算。采样环节的衰减增益从直觉上可以这样来看，采样引脚的2.5V代表实际输出25V电压，因此缩小了十倍。从模拟控制上来讲，这里的增益系数就是1/10。但是在数字系统来看，采样进去的数字量通常不会直接拿来做控制，一般是先要转换为实际值(代表实际物理意义)来做控制。用实际值做控制的好处就是代码更易于理解，更符合人类的直觉。

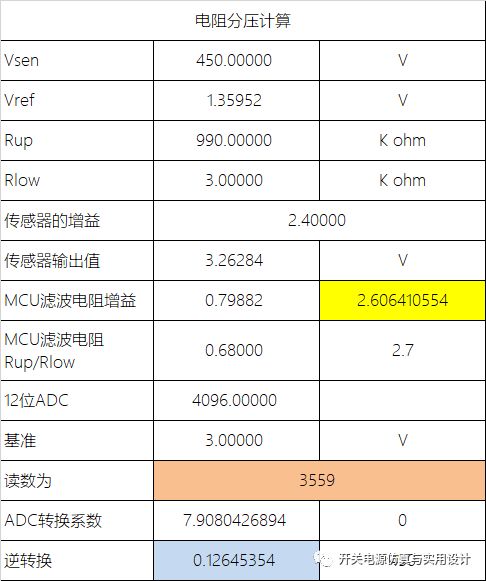
  所以，如果把采样的数字量转换为实际电压电流后，就消除了分压电阻和采样这一块带来的增益衰减或放大。但是ADC引脚通常不会是直连到输出端，一般情况下还会经过信号调理电路。信号调理电路中会引入低通滤波或差分放大等操作，这些操作就会导致信号调理这边多了个滤波器的传递函数被引入控制环路中。在考虑闭环系统时就不得不考虑这个滤波器带来的增益衰减或相位延迟，带宽过低的差分放大滤波器会明显影响到闭环的带宽。从工程直觉来看，滤波器的带宽最好5-10倍频率高于系统闭环带宽，避免产较生较大的相位移恶化系统的相位余量。

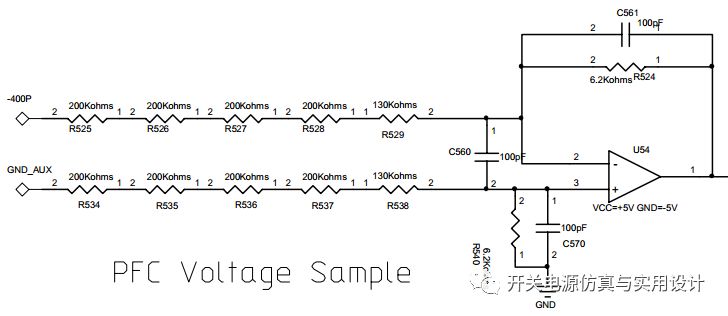
   PWM模块的增益：如果PWM周期寄存器的值是1000，在100MHz主频时，对应100KHZ开关频率。因此PWM增益可以简化为1/PWM。与模拟控制不同之处是模拟控制的PWM周期最大值一般就5V，最大增益仅为0.2。综上所述，即可以获得BUCK功率级的控制-输出的传递函数。但是上文中从模拟过渡到数字的控制方法是直接离散到Z域的，并没有实际考虑系统中存在的零阶保持器的影响，从而导致实际系统的闭环性能要比预期的设计结果差。如果考虑零阶保持器的影响，则功率级的传递函数需要引入ZOH的影响，ZOH的传递函数为：

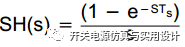
  系统延迟用Hc表示，其传递函数为：

，代表着从ADC采样时刻到PWM更新占空比的系统延迟，用延迟时间Td表示，这里包含了ADC的转换事件，数字控制器的计算事件，更新PWM载入所需时间等等。数字PWM部分的信号重构由零阶保持器ZOH表示：

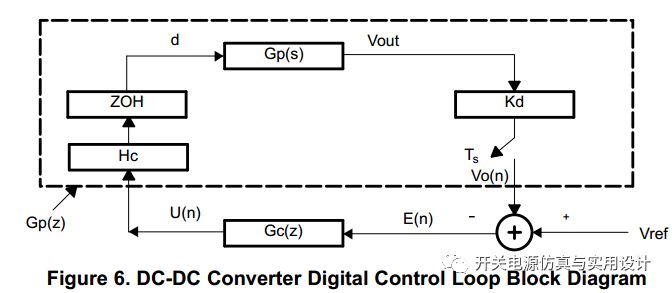
  上图的虚线部分可以归一成离散的控制到输出的传递函数，可以简化表示离散DCDC控制系统，从而可以直接在Z域进行闭环设计。

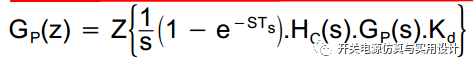
   得到z域传递函数之后简单的操作的方法就是，将离散后的传递函数写入到sisotool中，matlab可以辅助输出闭环控制器的传递函数。而且是直接输出Z域差分方程，简单的提取系数就可以写入控制程序，完成了闭环控制器的设计，然后就可以通过仿真或实际测试来验证闭环性能了。

  下面是.m文件，表述了具体的设计过程：

% BUCK SISO TF

%时间：2019年05月18日

clear all;

echo off

clc 

% TF:

Vin = 18;     %buck input voltage     

Vo = 14;      %buck output voltage       

Io = 25;      %buck output current   

Vadc_max = 1;

Kd = 1/ Vadc_max;    

pwm_max = 100;

gf_pwm = 1/pwm_max;

L = 1e-6;       %buck Lf

C = 810e-6;     %buck Cout 

Rc = 1e-3;      %buck Cout esr

RL = Vo/Io;     %buck Rload

Ts = 10e-6;     %buck controle Ts

Td = 0.0 * Ts;  %buck controle Tdelay

Td_h = 0.5 * Ts;

Td_one = 1 * Ts;

Td_two = 2 * Ts;

num_Gps = gf_pwm * Vin * [Rc*C 1]; 

denom_Gps = [L * C * (1 + Rc/RL) (L/RL + Rc*C) 1];
 Gps_dly = tf(num_Gps, denom_Gps, 'inputdelay' , Td);  %s-domain plant with computation delay Td%
Gpz = c2d(Gps_dly * Kd, Ts, 'zoh');                   %Discrete plant with ZOH, Kd and Td%

num_c = 0.050261 * conv([1 -0.5681], [1 -0.2523]);

den_c = conv( [1 -1], conv([1 -0.7569], [1 -0.7028]));

Gc = tf(num_c, den_c, Ts)

Gc_z = tf(num_c, den_c, Ts,'variable','z^-1')

Tvloop = Gc * Gpz

x = bodeplot(Tvloop,Gc, Gpz)  %打印bode图,从10 ~ 1000K

grid on; 

setoptions(x,'FreqUnits','Hz','PhaseVisible','on');

title('Tvloop(z)') 

输出考虑ZOH和系统延迟后的离散传递函数bode图：

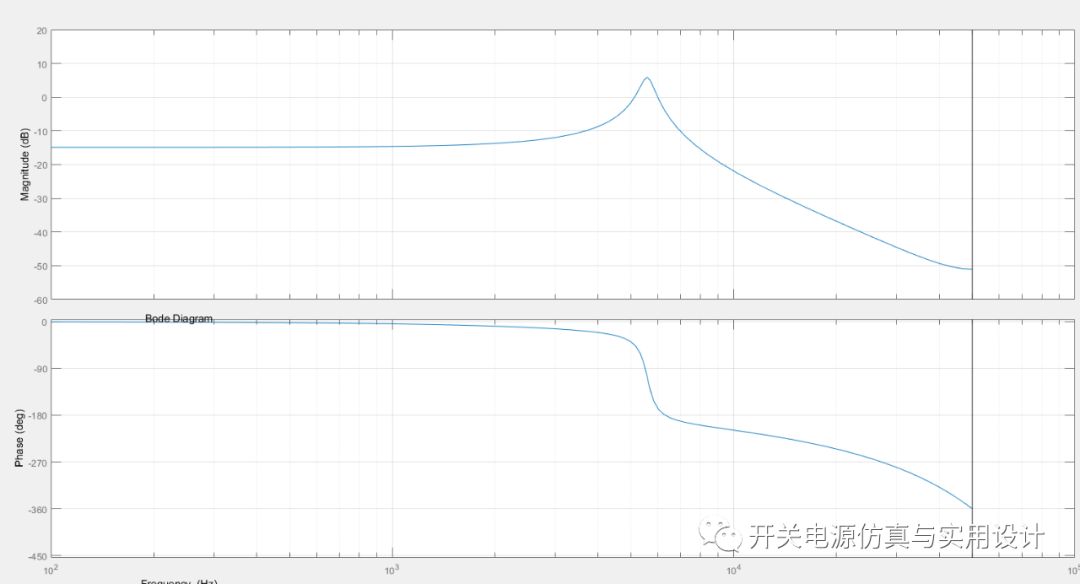
作为对比，同样的参数在plecs中的输出结果：

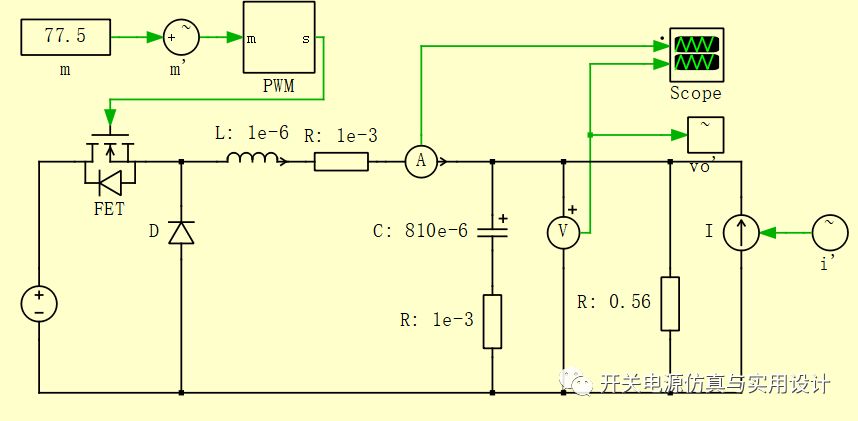
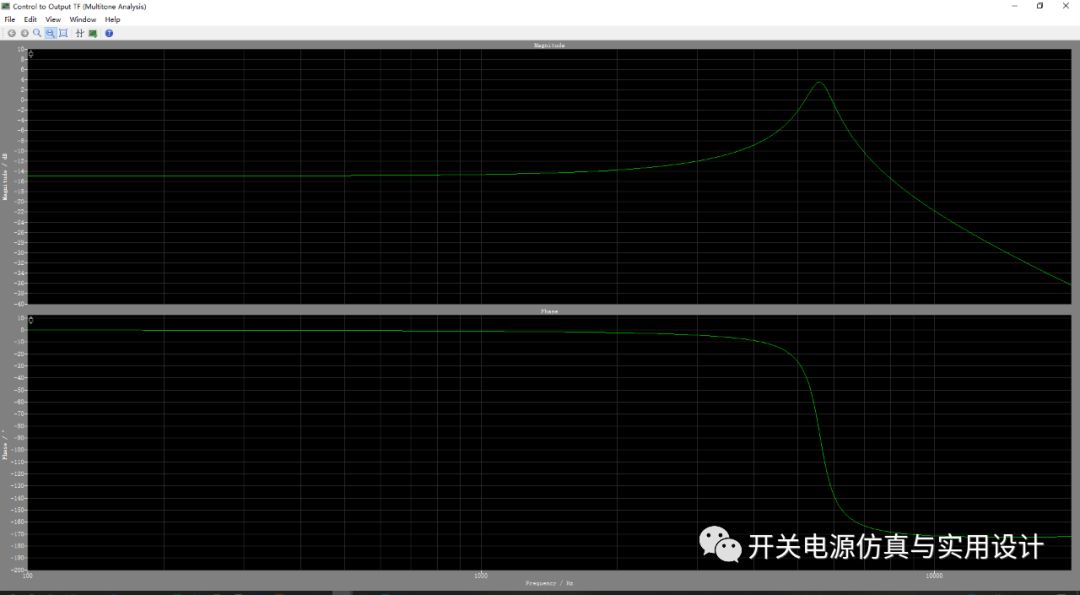
可见，几乎是一样的，可以说明上述分析方法的准确性。
利用sisitool得到的闭环控制器的传递函数：

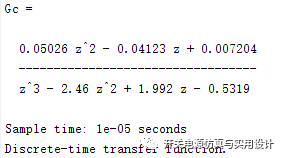
最后验证环路整体的开环传递函数，用于判定稳定性。

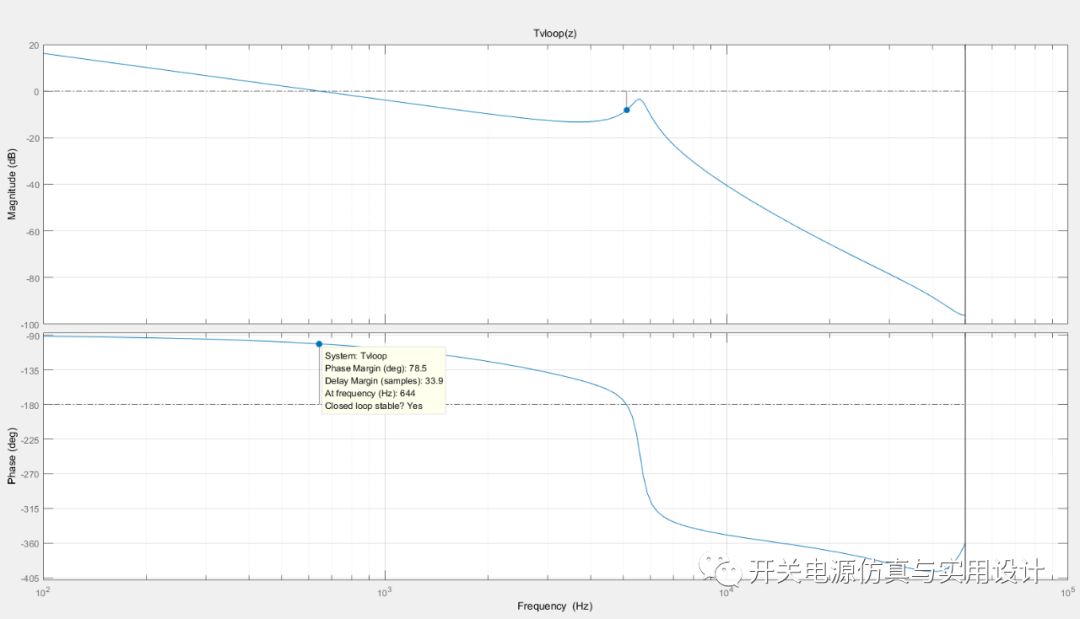
参考文档：
1 .Designing a TMS320F280x Based Digitally Controlled DC-DC Switching Power Supply  

最后觉得文章写的不错，就关注一波吧。