概述
一阶RC低通滤波电路数字化
- 1. 一阶RC电路
- 1.1 电路图
- 1.2 时域表达式
- 1.3 传递函数
- 1.4 Z Z Z变化 & 差分方程
- 1.5 一阶RC数字滤波器的基本算法
1. 一阶RC电路
1.1 电路图
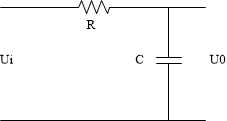其中，
R
R
R为滤波电阻，
C
C
C为滤波电容，
U
i
U_{i}
Ui为输入电压，
U
0
U_{0}
U0为输出电压。
1.2 时域表达式
U 0 = U i − R C d U 0 d t U_{0} = U_{i} - RCfrac{dU_{0}}{dt} U0=Ui−RCdtdU0
1.3 传递函数
同时求拉氏变换，在零初始条件下可得：
U
0
(
s
)
=
U
i
(
s
)
−
R
C
s
U
0
U_{0}(s)=U_{i}(s)-RCsU_{0}
U0(s)=Ui(s)−RCsU0
则传递函数：
G
(
s
)
=
U
0
(
s
)
U
i
(
s
)
=
1
1
+
R
C
s
G(s) = frac{U_{0}(s)}{U_{i}(s)}=frac{1}{1+RCs}
G(s)=Ui(s)U0(s)=1+RCs1
1.4 Z Z Z变化 & 差分方程
已知传递函数，可利用双线性变换、一阶前向差分和一阶后向差分等方式求取
Z
Z
Z函数。
(1) 一阶后向差分
s
=
1
−
z
−
1
T
s=frac{1-z^{-1}}{T}
s=T1−z−1
其中，
T
T
T为离散周期，也就是采样周期。
写成
Z
Z
Z函数为：
Y
(
Z
)
=
T
T
+
R
C
X
(
Z
)
+
R
C
T
+
R
C
Y
(
Z
)
Z
−
1
Y(Z) = frac{T}{T+RC}X(Z)+frac{RC}{T+RC}Y(Z)Z^{-1}
Y(Z)=T+RCTX(Z)+T+RCRCY(Z)Z−1
写成差分方程为：
y
(
n
)
=
T
T
+
R
C
x
(
n
)
+
R
C
T
+
R
C
y
(
n
−
1
)
y(n) = frac{T}{T+RC}x(n)+frac{RC}{T+RC}y(n-1)
y(n)=T+RCTx(n)+T+RCRCy(n−1)
(2) 双线性变换
s
=
2
T
1
−
Z
−
1
1
+
Z
−
1
s = frac{2}{T} frac{1-Z^{-1}}{1+Z^{-1}}
s=T21+Z−11−Z−1
写成
Z
Z
Z函数为：
Y
(
Z
)
=
T
T
+
2
R
C
X
(
Z
)
+
T
T
+
2
R
C
Z
−
1
X
(
Z
)
+
2
R
C
−
T
T
+
2
R
C
Z
−
1
Y
(
Z
)
Y(Z) = frac{T}{T+2RC}X(Z) + frac{T}{T+2RC}Z^{-1}X(Z)+frac{2RC-T}{T+2RC}Z^{-1}Y(Z)
Y(Z)=T+2RCTX(Z)+T+2RCTZ−1X(Z)+T+2RC2RC−TZ−1Y(Z)
1.5 一阶RC数字滤波器的基本算法
按照一阶差分方程的形式：
y
(
n
)
=
a
∗
x
(
n
)
+
(
1
−
a
)
∗
y
(
n
−
1
)
y(n) = a * x(n) + (1 - a)*y(n-1)
y(n)=a∗x(n)+(1−a)∗y(n−1)
其中，
a
a
a是一个和采样周期及RC有关的参数：
a
=
T
T
+
R
C
a = frac{T}{T+RC}
a=T+RCT
a为小于1的数，在实际可以通过右移的方式实现。
1
a
=
T
+
R
C
T
=
1
+
R
C
T
frac{1}{a} = frac{T+RC}{T} =1+ frac{RC}{T}
a1=TT+RC=1+TRC
此时，根据RC电路截止频率公式计算可得：
f
L
=
1
2
π
R
C
=
a
2
π
T
(
1
−
a
)
f_{L} =frac{1}{2 pi RC}= frac{a}{2pi T(1-a)}
fL=2πRC1=2πT(1−a)a
根据RC电路延迟时间公式计算可得：
t
τ
=
R
C
=
(
1
a
−
1
)
T
t_{tau}=RC=(frac{1}{a}-1)T
tτ=RC=(a1−1)T
最后
以上就是忧虑黑米为你收集整理的一阶RC低通滤波电路数字化1. 一阶RC电路的全部内容，希望文章能够帮你解决一阶RC低通滤波电路数字化1. 一阶RC电路所遇到的程序开发问题。
如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。
发表评论 取消回复