二进制与格雷码转换

1，格雷码原理：

格雷码因其相邻两个数之间的bit位有且只有一位发生变化，故常作用于多bit数据同步打拍，如下图所示：

如图所示，二进制数1和2,3和4,5和6,7和0都是相邻的数，且相邻数不同于多bit，而对应的格雷码却只相差1bit。

2，二进制转格雷码（bin2gray）

（1）最高bit保持不变

（2）当前bit与高一bit亦或得当前格雷码，gray[i] = bin[i] ^ bin[i+1]，i为0~N-1

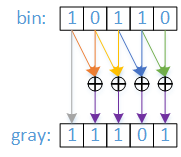
如上图，gray[4] = bin[4] = 1, 

                gray[3] = bin[4] ^ bin[3] = 1 ^ 0 = 1

                gray[2] = bin[3] ^ bin[2] = 0 ^ 1 = 1

                gray[1] = bin[2] ^ bin[1] = 1 ^ 1 = 0

                gray[0] = bin[1] ^ bin[0] = 1 ^ 0 = 1

                故输入bin = 10110，输出gray = 11101

（3）RTL实现

        输入bin[N:0], 输出gray[N:0]

        a，循环

always @(*) begin
  integer i;
  gray[N-1] = bin[N-1];
  for(i=0; i<N-1; i=i+1) begin
	gray[i] = bin[i+1] ^ bin[i]
  end
end

        b，移位寄存器

assign gray[N-1:0] = (bin[N-1:0] >> 1) ^ bin[N-1:0];

3，格雷码转二进制（gray2bin）

（1）最高bit保持不变

（2）当前bit与高一bit格雷码亦或得当前格雷码，gray[i] = bin[i] ^ gray[i+1]，i为0~N-1

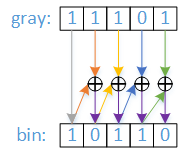
如上图，bin[4] = gray[4] = 1, 

                bin[3] = gray[4] ^ bin[3] = 1 ^ 1 = 0

                bin[2] = gray[3] ^ bin[2] = 0 ^ 1 = 1

                bin[1] = gray[2] ^ bin[1] = 1 ^ 0 = 1

                bin[0] = gray[1] ^ bin[0] = 1 ^ 1 = 0

                故输入bin = 11101，输出gray = 10110

（3）RTL实现

always @(*) begin
  integer i;
  bin[N-1] = gray[N-1];
  for(i=N-2; i>=0; i=i-1) begin
	bin[i] = bin[i+1] ^ gray[i]
  end
end

最后

以上就是痴情飞机为你收集整理的二进制与格雷码转换的全部内容，希望文章能够帮你解决二进制与格雷码转换所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。