[2018.10.13 T2] 工作计划

暂无链接

工作计划

【问题描述】

工作使艾奇快乐。
勤奋的工作为国家直接贡献了$GDP$，艾奇认为只要对国家有利，即使牺牲自
己生命也心甘情愿，绝不会因为自己可能受到祸害而躲开。
当艾奇无聊的时候，她就会去工作，然而并不是每次工作都是轻松而愉悦的。
当天艾奇又一次来到了学校，等待着她的是一个有$n$行$m$列的巨大的矩阵和$q$个任务。对于每个任务，艾奇被要求交换这个矩阵中的两个子矩阵。
每个任务，艾奇会获得六个正整数$x_1,y_1,x_2,y_2,h,w$。$x_1,y_1$代表了第一个矩阵左上角的行列位置（即在第$x_1$行第$y_1$列）；$x_2,y_2$代表了第二个矩阵左上角的行列位置，$h,w$代表了这两个矩阵的高和宽（即行数和列数）。
数据保证所有需要交换的矩阵互不相交或相邻。也就是说，没有任何一个元
素同时属于这两个矩阵，也不存在某两个元素分别属于两个矩阵且相邻（共边）。

【输入格式】

输入文件名为$havefun.in$。
第一行两个正整数$n,m,q$表示矩阵的高和宽（即行数和列数）和任务数。
接下来一行五个参数，将用于生成矩阵，详见备注。
接下来$q$行，每行$6$个数，$x_1,y_1,x_2,y_2,h,w$,分别表示第一个矩阵的左上位置，第二个矩阵的左上位置，这两个矩阵的高和宽（即行数和列数）。

【输出格式】

输出文件名为$havefun.out$。
输出一个数，将用于校验你的矩阵，详见备注。

【输入样例 1】

详见$havefun1.in$

【输出样例 1】

详见$havefun1.out$

【数据范围】

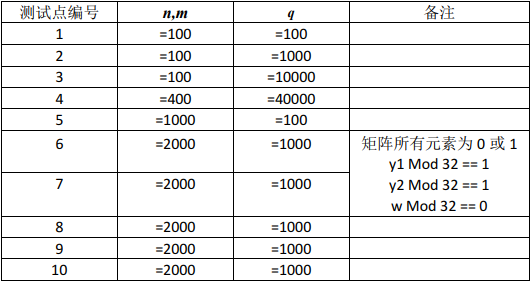
【备注】

由于读入规模较大，经过测试，在标准配置中，极限数据使用$scanf$读入需要约$1.35s$
所以我们决定，将读入矩阵的方式改为生成矩阵。我们将给你五个参数用于生成矩阵，$P,Q,R,S,Mod$。测试证明，这段代码在标准配置中，极限数据的生成只需要$0.12s$。你只需要调用$spawning$ 函数，并申请一个至少为$2005\times 2005$的全局数组$A$接收即可，下标默认为$(1,1)$到$(n,m)$。输入保证$P,Q,R,S,Mod<10^9$。
你必须保证数组$A$中所有元素为$0$，矩阵的长宽即$n,m$为全局变量。
当然，输出矩阵也是非常缓慢的。请你将你的答案全部赋值给全局数组$A$矩阵，并调用$checker$函数，你的主程序中不需要输出任何多余信息。
你并不需要对样例三中的答案为负数感到惊讶或担心。给出的$checker$函数在极限数据下计算本身就是超出$longlong$范围的。但凡你的最终矩阵是正的，该函数就会输出一个正确的结果。
我们已经将这两段生成代码以文件形式下发，文件名为$Too\_young.cpp$

题解

用一个包含上下左右四个方向的链表维护矩阵即可，访问元素时记得爬链表，不能直接调用。

代码

警告：这份代码常数极大，仅供参考

#include<cstdio>
#include<algorithm>
using namespace std;
const int M=2005;
struct sd{int x,y;}w[M][M],a[M][M],s[M][M],d[M][M];
int A[M][M],ans[M][M],n,m,q,P,Q,R,S,Mod;
void spawning(int P,int Q,int R,int S,int Mod){
	int T=0;
	for(int i=1;i<=n;i++)
		for(int j=1;j<=m;j++){
			T=(T+(1ll*(i+j)*P+1ll*i*j*Q+1ll*i*R+1ll*j*S)%Mod+Mod)%Mod;
			A[i][j]=T;
		}
	A[P%n+1][P%m+1]^=1;A[P%n+1][Q%m+1]^=1;A[P%n+1][R%m+1]^=1;A[P%n+1][S%m+1]^=1;
	A[Q%n+1][P%m+1]^=1;A[Q%n+1][Q%m+1]^=1;A[Q%n+1][R%m+1]^=1;A[Q%n+1][S%m+1]^=1;
	A[R%n+1][P%m+1]^=1;A[R%n+1][Q%m+1]^=1;A[R%n+1][R%m+1]^=1;A[R%n+1][S%m+1]^=1;
	A[S%n+1][P%m+1]^=1;A[S%n+1][Q%m+1]^=1;A[S%n+1][R%m+1]^=1;A[S%n+1][S%m+1]^=1;
}
void checker(){
	long long Pin=0;
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			Pin+=(1ll*i*n+j)*A[i][j];
		}
	}printf("%lldn",Pin);
}
void in(){scanf("%d%d%d%d%d%d%d%d",&n,&m,&q,&P,&Q,&R,&S,&Mod);}
void ac()
{
	spawning(P,Q,R,S,Mod);
	for(int i=1;i<=n;++i)for(int j=1;j<=m;++j)w[i][j]=(sd){i-1,j},a[i][j]=(sd){i,j-1},s[i][j]=(sd){i+1,j},d[i][j]=(sd){i,j+1};
	for(int i=1;i<=n;++i)d[i][0]=(sd){i,1},a[i][m+1]=(sd){i,m};
	for(int i=1;i<=m;++i)s[0][i]=(sd){1,i},w[n+1][i]=(sd){n,i};
	for(int x1,y1,x2,y2,h,b,i;q--;)
	{
		scanf("%d%d%d%d%d%d",&x1,&y1,&x2,&y2,&h,&b);
		sd sq1=(sd){x1,0},sq2=(sd){x2,0};
		for(i=1;i<=y1;++i)sq1=d[sq1.x][sq1.y];
		for(i=1;i<=y2;++i)sq2=d[sq2.x][sq2.y];
		swap(d[a[sq1.x][sq1.y].x][a[sq1.x][sq1.y].y],d[a[sq2.x][sq2.y].x][a[sq2.x][sq2.y].y]);
		swap(a[sq1.x][sq1.y],a[sq2.x][sq2.y]);
		for(i=1;i<h;++i)
		{
			sq1=s[sq1.x][sq1.y];sq2=s[sq2.x][sq2.y];
			swap(d[a[sq1.x][sq1.y].x][a[sq1.x][sq1.y].y],d[a[sq2.x][sq2.y].x][a[sq2.x][sq2.y].y]);
			swap(a[sq1.x][sq1.y],a[sq2.x][sq2.y]);
		}
		swap(w[s[sq1.x][sq1.y].x][s[sq1.x][sq1.y].y],w[s[sq2.x][sq2.y].x][s[sq2.x][sq2.y].y]);
		swap(s[sq1.x][sq1.y],s[sq2.x][sq2.y]);
		for(i=1;i<b;++i)
		{
			sq1=d[sq1.x][sq1.y],sq2=d[sq2.x][sq2.y];
			swap(w[s[sq1.x][sq1.y].x][s[sq1.x][sq1.y].y],w[s[sq2.x][sq2.y].x][s[sq2.x][sq2.y].y]);
			swap(s[sq1.x][sq1.y],s[sq2.x][sq2.y]);
		}
		swap(a[d[sq1.x][sq1.y].x][d[sq1.x][sq1.y].y],a[d[sq2.x][sq2.y].x][d[sq2.x][sq2.y].y]);
		swap(d[sq1.x][sq1.y],d[sq2.x][sq2.y]);
		for(i=1;i<h;++i)
		{
			sq1=w[sq1.x][sq1.y];sq2=w[sq2.x][sq2.y];
			swap(a[d[sq1.x][sq1.y].x][d[sq1.x][sq1.y].y],a[d[sq2.x][sq2.y].x][d[sq2.x][sq2.y].y]);
			swap(d[sq1.x][sq1.y],d[sq2.x][sq2.y]);			
		}
		swap(s[w[sq1.x][sq1.y].x][w[sq1.x][sq1.y].y],s[w[sq2.x][sq2.y].x][w[sq2.x][sq2.y].y]);
		swap(w[sq1.x][sq1.y],w[sq2.x][sq2.y]);
		for(i=1;i<b;++i)
		{
			sq1=a[sq1.x][sq1.y],sq2=a[sq2.x][sq2.y];
			swap(s[w[sq1.x][sq1.y].x][w[sq1.x][sq1.y].y],s[w[sq2.x][sq2.y].x][w[sq2.x][sq2.y].y]);
			swap(w[sq1.x][sq1.y],w[sq2.x][sq2.y]);
		}
	}
	for(int i=1;i<=n;++i)
	{
		sd pos=(sd){i,0};
		pos=d[pos.x][pos.y];
		for(int j=1;j<=m;++j)
		ans[i][j]=A[pos.x][pos.y],
		pos=d[pos.x][pos.y];
	}
	for(int i=1;i<=n;++i)for(int j=1;j<=m;++j)A[i][j]=ans[i][j];
	checker();
}
int main(){in(),ac();}

最后

以上就是聪慧彩虹为你收集整理的[2018.10.13 T2] 工作计划的全部内容，希望文章能够帮你解决[2018.10.13 T2] 工作计划所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。