奇异值分解SVD与在降维中的应用1. 特征值分解2 奇异值分解3 奇异值的意义4 奇异值究竟是什么？引用及参考文献

83 阅读 0 评论 55 点赞

我是靠谱客的博主含蓄蜡烛，最近开发中收集的这篇文章主要介绍奇异值分解SVD与在降维中的应用1. 特征值分解2 奇异值分解3 奇异值的意义4 奇异值究竟是什么？引用及参考文献，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

1. 特征值分解

1.1 特征值与特征向量

2 奇异值分解

3 奇异值的意义

4 奇异值究竟是什么？

引用及参考文献

1. 特征值分解

1.1 特征值与特征向量

特征值与特征向量定义如下：

$Ax=lambda x$

$A$ 是一个 $n*n$ 实对称矩阵， $x$ 是一个 $n$ 维向量，则 $lambda$ 是矩阵 $A$ 的一个特征值，而 $x$ 是矩阵 $A$ 的特征值 $lambda$ 所对应的特征向量。如果这些特征向量是线性无关的，即任意一个特征向量都不能被其他的向量的线性组合所表述出来，那么矩阵 $A$ 就可以特征分解，用以下式子表示：

$A=WvarSigma W^{-1}$

其中 $W$ 是这n个特征向量做组成的 $n*n$ 维矩阵，而 $varSigma$ 是以特征向量对应的 $n$ 特征值为对角线的 $n*n$ 维三角阵。将 $W$ 中的特征向量单位化，使得 $W^TW=I$ ，即 $W^T=W^{-1}$ ，故特征值分解也可以表达为：

$A=WvarSigma W^{T}$

征值分解，对矩阵有着较高的要求，它需要被分解的矩阵 $A$ 为实对称矩阵，对于一般的矩阵，例如： $m*n$ 的矩阵 $A$ ，不能用特征值分解，因此引出了奇异值分解。

2 奇异值分解

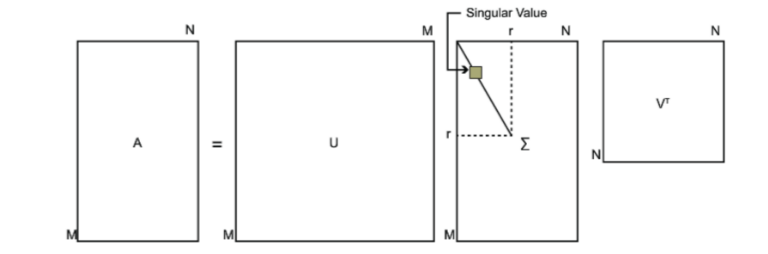
奇异值分解也是对矩阵进行分解的一种方法，当矩阵 $A$ 不是实对称矩阵时，就不可以使用特征值对矩阵进行分解。假设矩阵 $A$ 的形状是 $m*n$ ，使用奇异值分解的的表达式就是：

$A=UvarSigma V^{T}$

矩阵 $A$ 是待分解矩阵， $U$ 是 $m*m$ 的左奇异阵， $V$ 是 $n*n$ 的右奇异阵， $varSigma$ 是奇异值矩阵，主对角线上的元素叫做奇异值，并且以从大到小排序，奇异值以外的元素均为0。般我们将 $U$ 中的每个特征向量叫做 $A$ 的左奇异向量； $V$ 的列向量即是 $A^TA$ 的特征向量，一般我们将 $V$ 中的每个特征向量叫做 $A$ 的右奇异向量。

如何对矩阵进行奇异值分解呢？首先对 $A$ 进行操作，A是一个 $m*n$ 的矩阵， $A^TA$ 就会得到 $n*n$ 的对称方阵，因此就可以进行特征值分解，表达式如下：

$(A^TA)v_i=lambda_iv_i$

$v_i$ 是 $A^TA$ 的特征向量，由 $v_i$ 构成的就是右奇异阵 $V$ ， $v_i$ 被称作右奇异向量。同理 AA^T 也是对称方阵，形状是 $m*m$ ，同样对其特征值分解，表达式如下：

$(AA^T)u_i=lambda_iu_i$

$u_i$ 是 AA^T 的特征向量，由 $u_i$ 构成的就是右奇异阵 $U$ ， $u_i$ 被称作左奇异向量。其中 $U$ 和 $V$ 都是酉矩阵，即 $U^TU=E$ ， $V^TV=E$ ，则 $V^T=V^{-1}$ 。奇异值阵除了主对角线以外都是0，设奇异值为 $sigma$ ，因此我们可以根据 $U$ 和 $V$ 求出奇异值矩阵，推导如下：

$A=UvarSigma V^{T}$

$AV=UvarSigma$

$Av_i=sigma_iu_i$

$sigma_i = frac{Av_i}{u_i}$

奇异值也可以根据矩阵 $A^TA$ 的特征值是矩阵 $A$ 的奇异值的平方来求： $sigma_i =sqrt{lambda_i}$ ，从直觉上很好理解，因为 $A^TA$ 相当于是矩阵 $A$ 的平方，某种程度上讲奇异值是特殊的特征值，所以 $A^TA$ 的特征值是矩阵 $A$ 的奇异值的平方，可以这么记，但是严格的数学证明我还不知道是如何证明的。

3 奇异值的意义

奇异值与特征值类似，可以使用奇异值或特征值度量矩阵信息，使用一阶范数或者二阶范数的平方度量矩阵信息，也就是奇异值之和或者奇异值的平方和。而奇异值矩阵是列向量是按照奇异值的大到小排列的，且奇异值下降速度很快，往往前几个奇异值就占据了奇异值总和中大部分的权重，也就是说，可以使用前几个列向量近似代表原矩阵，这样损失不会很大，且又节省了大部分空间，也可以起到降维的效果，这就是所说的SVD用于降维的主要思想。

由于这个重要的性质，SVD可以用于PCA降维，来做数据压缩和去噪。也可以用于推荐算法，将用户和喜好对应的矩阵做特征分解，进而得到隐含的用户需求来做推荐。同时也可以用于NLP中的算法，比如潜在语义索引（LSI）。

PCA降维是对于一组特征，计算出他们的协方差矩阵 $X^TX$ ，然后找到出最大的d个特征向量，组成矩阵在进行低维投影降维，但是当特征过多的时候协方差矩阵 $X^TX$ 的计算量很大。刘建平老师的博客中提到SVD的实现算法可以不求先求出协方差矩阵 $X^TX$ ，也能求出右奇异矩阵 $V$ ，这样在特征数很大的时候非常有效。

在降维的时候只用了右奇异阵，来对原矩阵降维，实际上左奇异阵与原矩阵左乘起到的作用是减少行数，右奇异阵与原矩阵右乘的作用是减少列数，也就是减少原矩阵的特征向量，起到降维的效果。