后记

虽然写在最前面，但是这个其实是考完以后的记录。

先说结果，都过了，而且两门课都在 80 左右（一上一下）。
这学期课没去过几次，考前两门课加起来复习了一个星期，结果算不错啦。

一开始这篇博客只有矩阵论相关资料，后来把数理统计补上了（数理统计资料比较少）

好歹也是对努力学习这两门课（一个星期）的收获的记录 ????

最后说一下，学校的打印店挺坑的诶，感觉往年卷子几乎没有参考价值的（较老年份），基本上看我发到网盘里的资料就可以了。实在想买就当花钱买个心安咯~

矩阵论

这份笔记应该只适用于2021年的江苏大学矩阵论期末考试…

如果后面有学弟学妹们看见，可以参考一下，不过主要还是要看你们那一年的复习题。

这是我复习时的一些资料（师兄们传下来的，以及我自己收集的，还有老师发的课件和题目…），学弟学妹们记得传承下去：矩阵论资料

网上找到的，别人整理的一些知识点（非江苏大学），有些知识点可以用上：

• 矩阵论期末考试（一）
• 矩阵论期末考试（二）

求基与维数

一些名词解释：

• span 可以理解为 “生成”， s p a n { a 1 , a 2 , . . . , a n } span{a_1,a_2,...,a_n} span{a1​,a2​,...,an​} 表示以 $a_1,a_2,...,a_n$ 为基的向量空间，就是形如 $k_1{a}_1＋k_2{a}_2＋\dots \dots ＋k_n{a}_n$，$k_i$ 是任意实数的向量的集合

• 基：一组线性无关的向量集，可以生成给出的子空间

• 维数 - dim：基中含有向量的个数，即线性无关的向量的个数，即秩

• 求 $V_1+V_2$ 的情况很简单，$V_1\cap V_2$ 记住套路就行：设一个 x 满足 V1、V2 线性关系

  注意：一般 $dim(V_1\cap V_2)$ 好像都等于 1

题目1 - 课堂 pdf

题目2 - 课堂pdf

这题的难点在于没有直接给出 $V_1$ 的基，所以要先求 $V_1$ 的基

求 $V_1$ 的基也很简单，就是移个项，将某个变量用其他变量表示，然后给其他变量01赋值即可

题目3 - 复习题A

题目4 - 矩阵论.doc

求 $\rho (a)$ 、$cond(A{)}_{\infty }$ 、收敛和、高次多项式

矩阵论三种常见的范数，我们主要用的无穷范数（行和范数）、1-范数（列和范数）

一些笔记：

• $\rho (a)$ 就是谱半径，就是特征值绝对值（如果复数则取模）中的最大值

如果矩阵的特征值是复数，取模：谱半径 = 根号下 实部^2 + 虚部^2

• 无穷范数（行和范数） $||A|{|}_{\infty }$ 就是沿行方向取绝对值求和，取最大值

  $||A^{-1}|{|}_{\infty }$ 对 A 求逆后，同理

  1-范数（列和范数） $||A|{|}_1$ 就是沿列方向取绝对值求和，取最大值

• 条件数 $cond(A)$ 等于A的无穷范数与$A^{-1}$的无穷范数的乘积

• 判断矩阵是否收敛： 谱半径 < 1，则收敛

  也可以对谱半径的范围进行 估计，谱半径 <= $||A|{|}_{\infty }$、 谱半径 <= $||A|{|}_1$

• 判断矩阵级数（幂级数）是否收敛：谱半径 < 收敛半径，则收敛

  收敛半径 = $a_{k+1}/a_k$（$a_k$ 就是矩阵幂级数 $A^k$ 前面的那一块）

• 求矩阵幂级数和：先证明矩阵 B 收敛，然后套公式：级数和 = $(E-B{)}^{-1}$

解题笔记：

• 反正遇到这些题目就先求：特征值、特征向量
• 然后就按照套路做下去…

题目1 - 矩阵论.doc

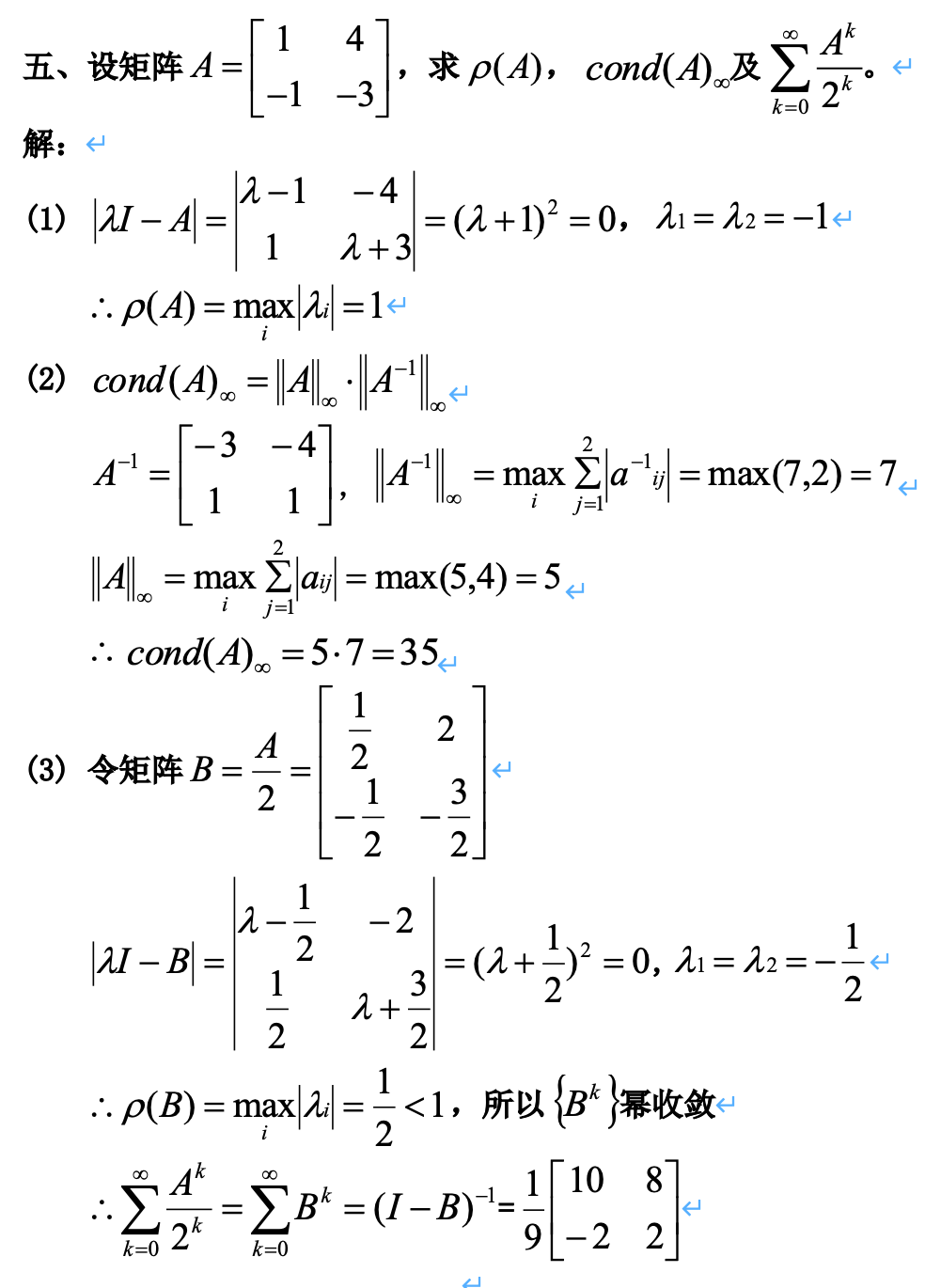
题目2 - 复习题A

求高次矩阵多项式 - 矩阵论.doc

一些笔记：

• 这个完全就是套路啊：大致步骤如下，结合例题，一下就懂了

  1、求特征多项式（关于 $\lambda$ 的多项式）

  2、把要求的式子中的矩阵，全部写作 $\lambda$

  3、长除法：要求的式子 / 特征多项式

  4、长除法得到余数，里把 $\lambda$ 换成矩阵，并计算

最大秩分解

一些笔记：

• 求最大秩分解也是套路，先把矩阵 A 化到标准形，同时得到 A 的秩 n

  然后，A 的前 n 列就是 B，A 的标准形的前 n 行就是 C，满足 A = BC

• 求 $A^{+}$，好像主要就是考：$A^{+}=C^{+}{B}^{+}=C^T(C{C}^T{)}^{-1}(B^{T}B{)}^{-1}{B}^T$

  

矩阵论.doc

复习题

对角化

一些笔记：

• 度量矩阵的求法：

题目1 - 矩阵论.doc

题目2 - 求基、度量矩阵 - 复习题A

QL分解、LU分解

行列式因子、不变因子、初等因子 可以参考这篇文章，很详细

一些笔记：

• 矩阵A可以进行LU分解的充要条件是：A的顺序主子式全不为0
• 行列式因子从 n -> 1 求，符号是 $D_n(\lambda )$；不变因子从 1 -> n 求，符号是 $d_n(\lambda )$

方法总结：

• 先写出 $\lambda E-A$

• 然后求行列式因子$D_n(\lambda )$ -> $D_1(\lambda )$

• 然后求不变因子：$d_1(\lambda )$ -> $d_n(\lambda )$，

  

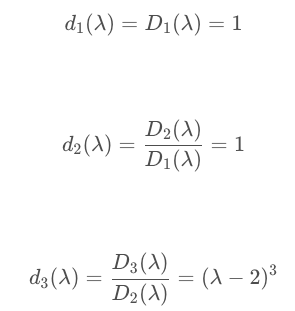
• 初等因子就是从不变因子开始找次项不为0的式子

• 已知初等因子求若当标准型要：

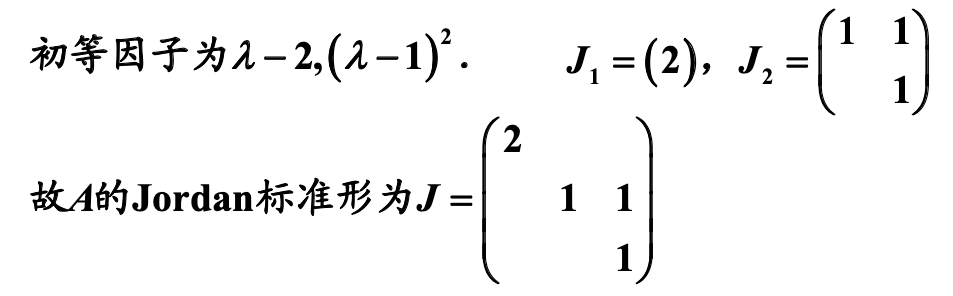
题目1 - 复习题 A

题目2 - 矩阵论.doc

矩阵论复习题（手写）

数理统计

复习资料： https://www.aliyundrive.com/s/Nc7x61UhdeX

如果是想刷题的话，看资料文件里面的 考试题库之 24 题（重要）.pdf，每年的考试题都是从这里出的（而且题目都不改），之前学长和我说我还不信，今年考了发现确实是这样。

课堂测验 文件夹里面的是今年老师课上做的测试题与答案，这个每年应该不一样。

以上两个比较重要，其他是一些常规资料：老师课件 + 课本 + 习题答案 …

数理统计复习笔记（手写）

可以参考一下，根据考试情况来说，我写的就是除了证明题意外所有的类型了。

最后

以上就是害怕长颈鹿为你收集整理的江苏大学矩阵论、数理统计期末考试复习后记矩阵论数理统计的全部内容，希望文章能够帮你解决江苏大学矩阵论、数理统计期末考试复习后记矩阵论数理统计所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。