二位数据可以表示矩阵的乘法，矩阵乘法的计算方法如下：
代码实现如下：
首先进行初始化工作：
复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35#include <stdio.h> #include <malloc.h> #include <stdlib.h> #define ROWS 4 #define COLUMNS 5 //定义行数和列数 typedef struct TwoDArray{ int rows; int columns; int** elements; } TwoDArray, *TwoDArrayPtr; //定义第二个矩阵 typedef struct TwoDStaticArray{ int rows; int columns; int elements[ROWS][COLUMNS]; } TwoDStaticArray, *TwoDStaticArrayPtr; //初始化矩阵。 TwoDArrayPtr initTwoDArray(int paraRows, int paraColumns){ int i; TwoDArrayPtr resultPtr = (TwoDArrayPtr)malloc(sizeof(struct TwoDArray)); resultPtr->rows = paraRows; resultPtr->columns = paraColumns; resultPtr->elements = (int**)malloc(paraRows * sizeof(int*)); for (i = 0; i < paraRows; i ++){ resultPtr->elements[i] = (int*)malloc(paraColumns * sizeof(int)); } return resultPtr; }
其次，随机分配元素到初始化好的矩阵当中，并且打印出来。
复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21//随机分配元素到矩阵里面。 void randomizeTwoDArray(TwoDArrayPtr paraPtr, int paraLowerBound, int paraUpperBound){ int i, j; for (i = 0; i < paraPtr->rows; i ++){ for (j = 0; j < paraPtr->columns; j ++) { paraPtr->elements[i][j] = rand() % (paraUpperBound - paraLowerBound) + paraLowerBound; } } } //打印矩阵。 void printTwoDArray(TwoDArrayPtr paraPtr){ int i, j; for (i = 0; i < paraPtr->rows; i ++){ for (j = 0; j < paraPtr->columns; j ++) { printf("%d, ", paraPtr->elements[i][j]); } printf("rn"); } }
接下来设计乘积函数，首先判断是否满足乘积的条件（第一个矩阵的列数不等于第二个矩阵的行数则无法计算）
然后开始循环嵌套计算矩阵的乘法
复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23//设计乘积函数 TwoDArrayPtr matrixMultiply(TwoDArrayPtr paraPtr1, TwoDArrayPtr paraPtr2){ int i, j, k, sum; if (paraPtr1->columns != paraPtr2->rows){ printf("Matrices cannot be multiplied.rn"); return NULL; } TwoDArrayPtr resultPtr = initTwoDArray(paraPtr1->rows, paraPtr2->columns); for (i = 0; i < paraPtr1->rows; i ++){ for (j = 0; j < paraPtr2->columns; j ++) { sum = 0; for (k = 0; k < paraPtr1->columns; k ++) { sum += paraPtr1->elements[i][k] * paraPtr2->elements[k][j]; } resultPtr->elements[i][j] = sum; printf("sum = %d, ", sum); } } return resultPtr; }
最后进行测试：
复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43//测试函数 void twoDArrayTest(){ TwoDArrayPtr tempPtr1, tempPtr2, tempPtr3; tempPtr1 = initTwoDArray(3, 2); randomizeTwoDArray(tempPtr1, 1, 5); printf("The first matrix:rn"); printTwoDArray(tempPtr1); tempPtr2 = initTwoDArray(2, 4); randomizeTwoDArray(tempPtr2, 4, 9); printf("The second matrix:rn"); printTwoDArray(tempPtr2); tempPtr3 = matrixMultiply(tempPtr1, tempPtr2); printf("The result:rn"); printTwoDArray(tempPtr3); } //初始化第二个矩阵。 TwoDStaticArrayPtr initTwoDStaticArray(){ int i, j; TwoDStaticArrayPtr resultPtr = (TwoDStaticArrayPtr)malloc(sizeof(struct TwoDStaticArray)); resultPtr->rows = ROWS; resultPtr->columns = COLUMNS; for (i = 0; i < ROWS; i ++){ for (j = 0; j < COLUMNS; j ++) { resultPtr->elements[i][j] = i * 10 + j; printf("(%d, %d): %d; ", i, j, &(resultPtr->elements[i][j])); } } return resultPtr; } int main(){ twoDArrayTest(); TwoDStaticArrayPtr tempPtr = initTwoDStaticArray(); return 1; }
运行结果如下：
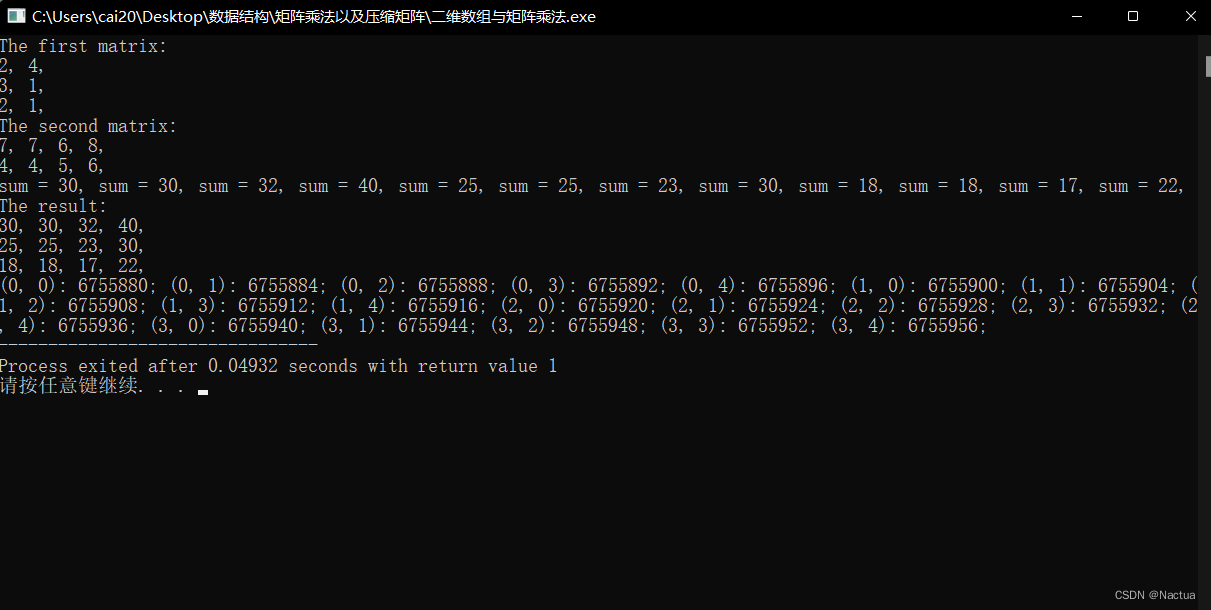
接下来是压缩矩阵的转置：
原理如下：
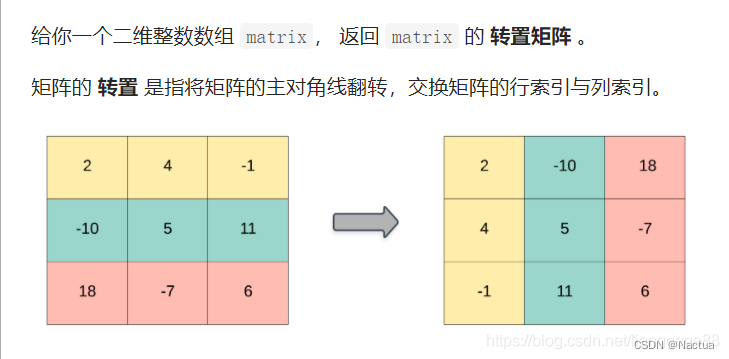
代码如下：
初始化工作：
复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35#include <stdio.h> #include <malloc.h> typedef int elem; //定义第一个矩阵结构体行数下标，列数下标，以及元素。 typedef struct Triple{ int i; int j; elem e; } Triple, *TriplePtr; //定义第二个矩阵结构体行数下标，列数下标，以及元素。 typedef struct CompressedMatrix{ int rows,columns,numElements; Triple* elements; } CompressedMatrix, *CompressedMatrixPtr; //初始化矩阵。 CompressedMatrixPtr initCompressedMatrix(int paraRows, int paraColumns, int paraElements, int** paraData){ int i; CompressedMatrixPtr resultPtr = (CompressedMatrixPtr)malloc(sizeof(struct CompressedMatrix)); resultPtr->rows = paraRows; resultPtr->columns = paraColumns; resultPtr->numElements = paraElements; resultPtr->elements = (TriplePtr)malloc(paraElements * sizeof(struct Triple)); for(i = 0; i < paraElements; i ++){ resultPtr->elements[i].i = paraData[i][0]; resultPtr->elements[i].j = paraData[i][1]; resultPtr->elements[i].e = paraData[i][2]; } return resultPtr; }
打印矩阵并进行压缩：
复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48//将矩阵打印出来 void printCompressedMatrix(CompressedMatrixPtr paraPtr){ int i; for(i = 0; i < paraPtr->numElements; i ++){ printf("(%d, %d): %drn", paraPtr->elements[i].i, paraPtr->elements[i].j, paraPtr->elements[i].e); } } //开始压缩 CompressedMatrixPtr transposeCompressedMatrix(CompressedMatrixPtr paraPtr){ //分配空间。 int i, tempColumn, tempPosition; int *tempColumnCounts = (int*)malloc(paraPtr->columns * sizeof(int)); int *tempOffsets = (int*)malloc(paraPtr->columns * sizeof(int)); for(i = 0; i < paraPtr->columns; i ++){ tempColumnCounts[i] = 0; } CompressedMatrixPtr resultPtr = (CompressedMatrixPtr)malloc(sizeof(struct CompressedMatrix)); resultPtr->rows = paraPtr->columns; resultPtr->columns = paraPtr->rows; resultPtr->numElements = paraPtr->numElements; resultPtr->elements = (TriplePtr)malloc(paraPtr->numElements * sizeof(struct Triple)); //扫描计算压缩的量。 for(i = 0; i < paraPtr->numElements; i ++) { tempColumnCounts[paraPtr->elements[i].j] ++; } tempOffsets[0] = 0; for(i = 1; i < paraPtr->columns; i ++){ tempOffsets[i] = tempOffsets[i - 1] + tempColumnCounts[i - 1]; printf("tempOffsets[%d] = %d rn", i, tempOffsets[i]); } //扫描另外一组数据。 for(i = 0; i < paraPtr->numElements; i ++) { tempColumn = paraPtr->elements[i].j; tempPosition = tempOffsets[tempColumn]; resultPtr->elements[tempPosition].i = paraPtr->elements[i].j; resultPtr->elements[tempPosition].j = paraPtr->elements[i].i; resultPtr->elements[tempPosition].e = paraPtr->elements[i].e; tempOffsets[tempColumn]++; } return resultPtr; }
最后设计测试函数：
复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36//设计测试矩阵函数。 void compressedMatrixTest(){ CompressedMatrixPtr tempPtr1, tempPtr2; int i, j, tempElements; //构建第一个矩阵。 tempElements = 4; int** tempMatrix1 = (int**)malloc(tempElements * sizeof(int*)); for(i = 0; i < tempElements; i ++){ tempMatrix1[i] = (int*)malloc(3 * sizeof(int)); } int tempMatrix2[4][3] = {{0, 0, 2}, {0, 2, 3}, {2, 0, 5}, {2, 1, 6}}; for(i = 0; i < tempElements; i ++){ for(j = 0; j < 3; j ++) { tempMatrix1[i][j] = tempMatrix2[i][j]; } } tempPtr1 = initCompressedMatrix(2, 3, 4, tempMatrix1); printf("After initialization.rn"); printCompressedMatrix(tempPtr1); tempPtr2 = transposeCompressedMatrix(tempPtr1); printf("After transpose.rn"); printCompressedMatrix(tempPtr2); } int main(){ compressedMatrixTest(); return 1; }
运行结果如下：
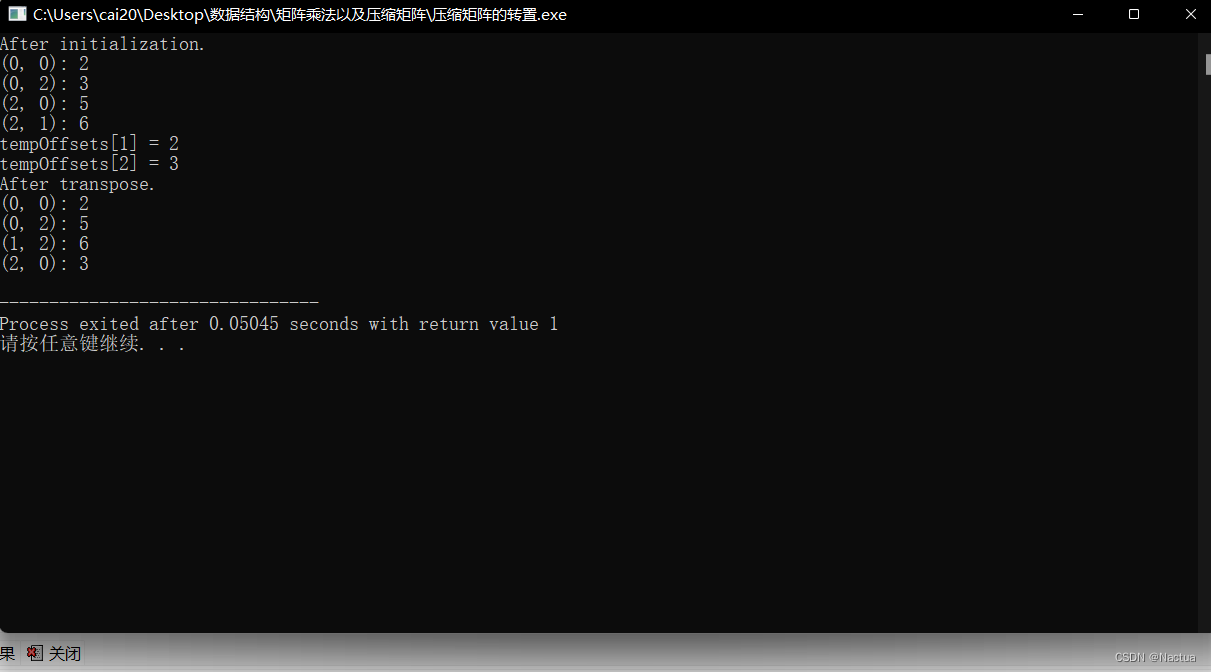
最后
以上就是伶俐画板最近收集整理的关于矩阵乘法以及压缩矩阵的转置的全部内容，更多相关矩阵乘法以及压缩矩阵内容请搜索靠谱客的其他文章。
本图文内容来源于网友提供，作为学习参考使用，或来自网络收集整理，版权属于原作者所有。
发表评论 取消回复