1.转置矩阵
1.1转置矩阵简介
把矩阵A的行换成同序数的列得到的新矩阵，叫做A的转置矩阵(Transpose of a Matrix)，记作ATAT。
例如：
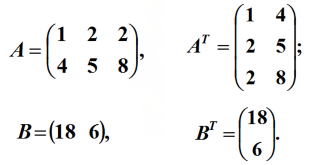
因此，转置矩阵的特点：
（1）转置矩阵的行数是原矩阵的列数，转置矩阵的列数是原矩阵的行数；
（2）转置矩阵下标（i，j）的元素对应于原矩阵下标（j，i）的元素。
1.2实现
使用二维数组作为矩阵的存储结构，根据转置矩阵的特点，很容易得到转置矩阵。
复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17/************************************************** *@para:matrix:原矩阵；row:矩阵行数；column:矩阵列数 *@ret:返回转置矩阵 **************************************************/ int** getTransposeMatrix(int** matrix,int row,int column){ int** matrixR=new int*[columns]; for(int i=0;i<columns;++i){ matrixR[i]=new int[rows]; } for(int i=0;i<row;++i){ for(int j=0;j<column;++j){ matrixR[j][i]=matrix[i][j]; } } return matrixR; }
2.矩阵相乘
2.1矩阵相乘简介
矩阵相乘的特点：
（1）当矩阵A的列数等于矩阵B的行数时，A与B才可以相乘。
（2）乘积C的第m行第n列的元素等于矩阵A的第m行的元素与矩阵B的第n列对应元素乘积之和。
（3）矩阵C的行数等于矩阵A的行数，C的列数等于B的列数。
2.2示例代码
复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14/******************************************** *@para:A:矩阵A；B:矩阵B；C:相乘结果矩阵；rowA：A的行数；columnB：B的列数；columnA：A的列数 *@ret:void ********************************************/ void matrixMul(int **A, int **B, int **C, int rowA, int columnB, int columnA){ for (int i=0;i<rowA;i++){ for (int j=0; j<columnB;j++){ C[i][j] = 0; for (int k=0;k<columnA;k++){ C[i][j]+=A[i][k]*B[k][j]; } } } }
3矩阵相乘后转置
一个矩阵的转置与它相乘，为什么是对称阵？
证明它们的乘积的转置等于其本身就可以了。(A^T*A)^T=A^T*(A^T)^T=A^T*A
参考文献
[1]转置矩阵 百度百科
[2]矩阵乘法 百度百科
最后
以上就是平淡鸡翅最近收集整理的关于矩阵转置与矩阵相乘1.转置矩阵1.2实现2.矩阵相乘3矩阵相乘后转置参考文献的全部内容，更多相关矩阵转置与矩阵相乘1内容请搜索靠谱客的其他文章。
本图文内容来源于网友提供，作为学习参考使用，或来自网络收集整理，版权属于原作者所有。
发表评论 取消回复