【鱼眼镜头4】[鱼眼畸变模型]：四阶多项式模型1 概述2 基于畸变直线斜率计算的校正算法具体过程实验结果与分析鱼眼镜头参考文献

92 阅读 0 评论 61 点赞

我是靠谱客的博主发嗲诺言，最近开发中收集的这篇文章主要介绍【鱼眼镜头4】[鱼眼畸变模型]：四阶多项式模型1 概述2 基于畸变直线斜率计算的校正算法具体过程实验结果与分析鱼眼镜头参考文献，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

为快速、高效地校正具有径向畸变的鱼眼图像，提出一种基于几何性质的校正算法。根据投影不变性原理以及径向畸变的几何特性，计算畸变直线的斜率，并通过求解线性方程组得出多项式校正模型的参数。实验结果表明，该算法能够以较低的运算复杂度获得较高的校正精度，相比于采用数学迭代拟合直线的方法，该算法在图像整体校正质量上有明显作用

在这里插入图片描述

1 概述

鱼眼镜头在获得大范围拍摄视角的同时，不可避免地引入了图像的径向(桶形)畸变，以解决在有限像面内容纳广角目标物体的问题[1]。

对于具有径向畸变的鱼眼图像的校正，主要分为基于鱼眼镜头标定的校准方法[2-3]和基于投影变换理论的校正方法[4-7]。

前者涉及真实世界坐标空间，鱼眼镜头坐标系以及平面成像坐标系之间的坐标转换，对于校准设备的精度要求较高。

后者基于投影不变性原理，通过迭代优化目标函数的方法得出校正模型的参数，从而完成对畸变图像的复原。

为简化迭代算法的复杂度，文献[7]提出一种基于数学代数的求解方案，在保证校正精度的情况下，通过 1 次迭代优化即可得到相应的校正参数。该方法虽然在一定程度上降低计算复杂度，但它依旧是基于目标函数优化的一种解决方案，计算复杂度仍然偏高。

基于上述分析，本文考虑径向畸变的固有几何特性，采用多项式校正模型，通过预先确定畸变直线的实际斜率求解校正模型的参数，并且通过缩放因子[7]解决畸变图像到校正图像之间的像素精度匹配问题。

2 基于畸变直线斜率计算的校正算法

2.1 基于投影不变性原理的校正模型建立

根据针孔相机的投影模型可知，空间直线 L 在二维成像面上的透视投影为平面直线 l。然而，鱼眼镜头为了囊括更大的视角，必须采用带有畸变的光学成像系统来建立视场到成像面的有限投影。

此时，空间直线 L 在鱼眼镜头下成像为一条曲线(畸变的直线)c。

鉴于上述分析，畸变校正函数应具有将畸变直线 c 校正为理想直线 l 的作用。考虑到径向畸变的特点，畸变像素点与校正像素点之间的映射关系可定义为

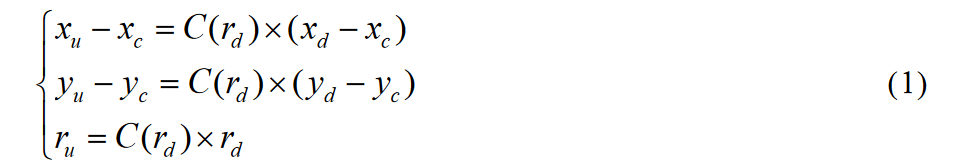
在这里插入图片描述

其中， $x_d,y_d)$ 与 $x_u,y_u)$ 分别表示畸变像素点与校正像素点的
坐标位置；

$r_d,r_u$ 分别为畸变像素点 $x_d ,y_d )$ 与校正像素点
$x_u ,y_u )$ 到畸变中心 $x_c, y_c)$ 的径向距离；
$C(r_d)$ 是校正函数，建立了从畸变像素点到校正像素点的位置映射关系。

根据径向畸变的特点，采用 4 阶奇次多项式校正模型即可取得理想
的校正效果[7]，故本文定义畸变校正函数

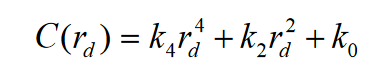
在这里插入图片描述

具体过程

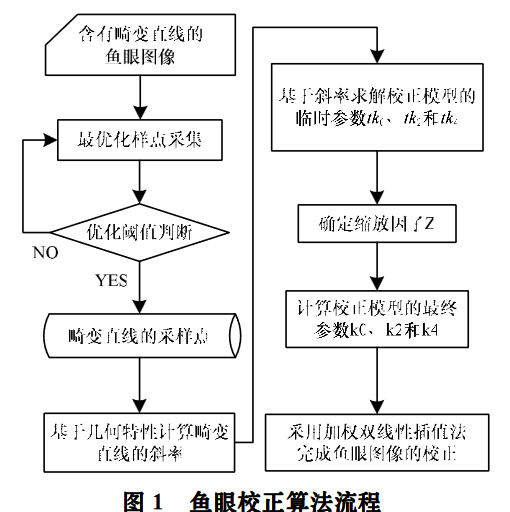
对于一幅含有畸变直线的鱼眼图像，

首先通过基于阈值判断的方法选取最优的采样点。
其次，根据采样点对，利用径向畸变的固有几何性质计算畸变直线的实际斜率，并由此联立线性方程组求解校正模型的临时参数值 $tk_0 、 tk_2 、 tk_4$
再次，根据畸变、校正点对距离和的最小化来确定缩放因子 Z，并由此得到最终的校正模型参数值 $k_0 、 k_2 、 k_4$ 。
最后，通过求解所得的校正函数 $C(r_d)$ ，采用加权双线性插值算法得到最终的校正图像。

在这里插入图片描述

2.2.1 畸变直线的斜率确定与临时参数的求解

(1)基于径向畸变的几何性质计算畸变直线的实际斜率K 。

图 2 为使用鱼眼镜头拍摄得到的 2 条畸变直线的示意图。本文不考虑鱼眼镜头主光轴发生偏心的情况，图像的畸变中心即可视为几何中心 $D_c(x_c ,y_c )$ 。

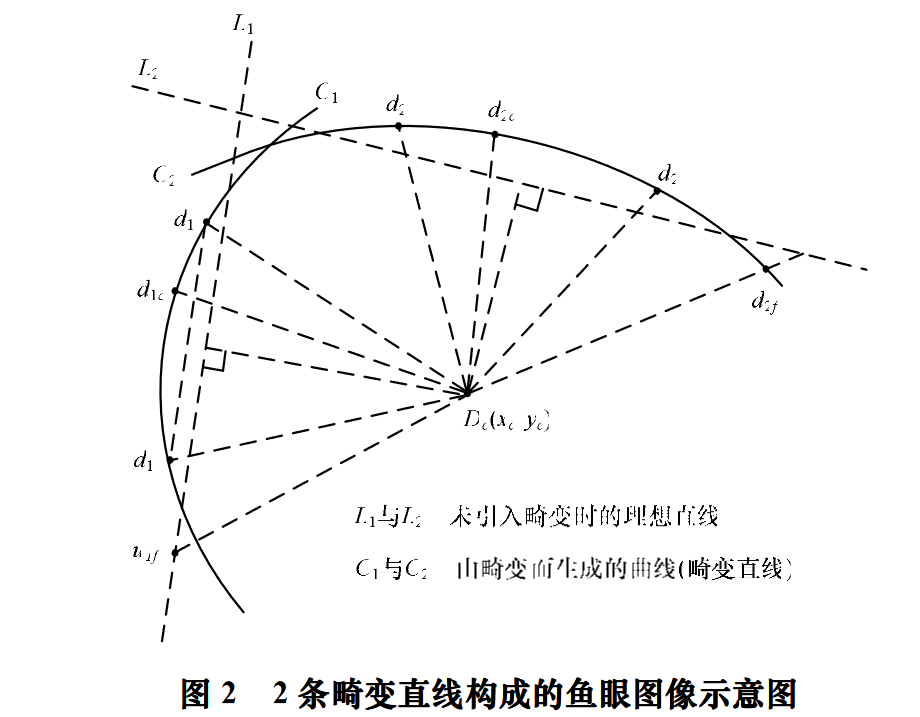
在这里插入图片描述

为求解理想直线 L 的实际斜率，由径向畸变的几何性质可知：

在理想直线 L 所对应的畸变直线 C 上取一组点对 d 与d’ ，若该点对到畸变中心 $D_c(x_c ,y_c )$ 的距离相等，则由此点对所构成的直线斜率即为理想直线 L 的实际斜率。

即畸变直线L1 的实际斜率 $K l 1$ 可由 d与d '两点坐标表示为 $y − y ′ x − x ′ frac{y-y'}{x-x'}$ 。

同理，由畸变点对 2d 与 d2’ 可得畸变直线 L2 的实际斜率 $K l 2$ 。

(2)基于畸变直线的实际斜率 K 求解校正模型的临时参数。对于校正模型的 3 个参数而言，通常可预设 $k_0 =1$ [7]，以避免平凡解的产生。本文将基于此设定而计算得到的参数称为临时参数，表示为 $tk_0 、 tk_2 、 tk_4$ 。因此，将临时畸变校正函数 $C (r)$ 表示为

在这里插入图片描述

由于 $tk_0$ 预设为 1，因此仅需构造一个二维线性方程组来求解 $tk_2 与 tk_4$ 。本文通过选取到畸变中心距离最近和最远的点对，基于计算得到的直线斜率构建线性方程组以求解临时参数值

在这里插入图片描述
式(4)中的坐标位置可由图 2 中的点 $d 1 c 、 d 1 f 、 d 2 c 、 d 2 f$ 分别通过式(3)，由式(1)得到

(3)取点优化与误差降低。考虑在畸变直线上取样点时所存在的误差，本文分别采用基于阈值优化和取多组点对的方法来降低取点误差及其对斜率计算的影响。

首先，在畸变直线上取样点时，只有同时满足如下 2 个阈值条件时，才会被视为可靠样点以用于后续计算。
阈值条件 1：取样点的灰度值为周边 8 邻域中最小，且小于 40(8 位灰度等级)。
阈值条件 2：取样点对到畸变中心的距离之差小于 0.3 个像素宽度。

其次，本文使用取多组点对的方式进一步减小斜率的计算误差。

由于取样误差的各向同性分布，因此而当选取点对的数目 N 增大时，取点误差对于斜率计算的影响比例下降，计算斜率更接近实际斜率。
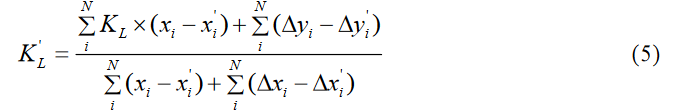
在这里插入图片描述

2.2.2 缩放因子的计算
为解决校正过程中的像素分辨率匹配问题，可采用缩放
因子 Z 来调节像素分辨率的匹配，具体应用请参考文献[7]。

实验结果与分析

实验选用基于直线拟合的梯度下降迭代算法 (gradient)[5] 和基于结果的代数算法(algebraic)[7]作为参照，对鱼眼图像中的畸变直线各取 8 个样点进行校正工作，并从算法复杂度、误差百分比以及主观视觉 3 个角度进行比较分析

校正算法的复杂度比较

表 1 给出校正采用多项式畸变模型鱼眼镜头拍摄得到的鱼眼图像时，3 种算法的运算量比较结果。其中，E、P、L 分别表示函数的计算次数，待解的多项式方程数目以及待解的线性方程组数目

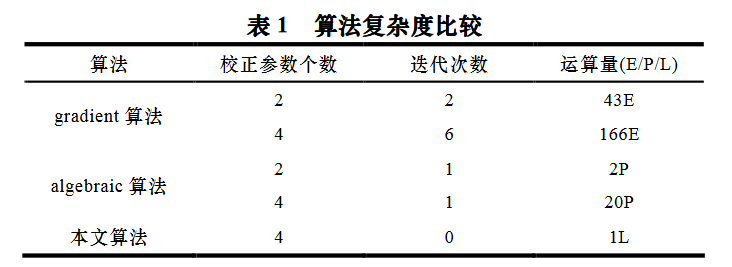
在这里插入图片描述

由表 1 可以看出，

gradient 算法在处理 2 阶与 4 阶多项式校正模型时，都需要进行多次函数计算以优化参数值。

algebraic 算法在处理 2 阶多项式校正模型时运算量较少，但是校正精度低，处理 4 阶多项式校正模型时，运算量便有明显提升。

本文算法在处理 4 阶多项式校正模型时无需任何迭
代计算，仅通过求解一个 2 维线性方程组即可得到校正模型
的参数值

鱼眼镜头

本文分别采用多项式模型和等距投影模型的鱼眼镜头生成不同类型的畸变图像。

评价指标

通过线性拟合度 D，
平均校正误差百分比 EA
以及最大校正误差百分比 EM
作为校正精度的评判标准。

D 值越小，表明畸变直线经过校正之后的线性度越好；
EA 值越小，表明校正模型与畸变模型越接近；
EM 值越小，表明校正后图像的整体感越好，无明显突兀区域，

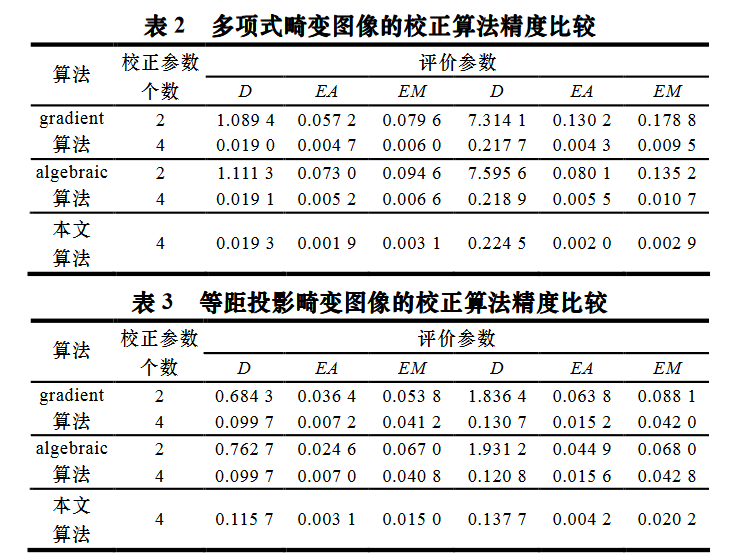
在这里插入图片描述

从表 2、表 3 可知，2 阶多项式校正模型的各项数值均不理想，校正误差明显。对于 4 阶多项式校正模型而言，与上述 2 种算法相比，本文算法在线性拟合度损失较小的情况下，校正误差降低明显。

主观视觉评价

本文以网格图像为评判标准，使用等距投影模型的鱼眼镜头生成畸变图像，并采用上述算法进行校正，结果见图 3。

可见，2 阶模型存在明显的校正过度，而采用 4 阶校正模型的 gradient 算法和 algebraic 算法虽然使较正图像中间区域的直线具有很好的线性度，但在网格图像的边缘存在校正不足。

相较而言，本文算法在获得接近于最佳线性拟合度的同时，改善了畸变图像边缘区域的视觉，图像的整体质量明显提升。

在这里插入图片描述

此外，本文分别使用多项式模型和等距投影模型的鱼眼镜头生成具有不同畸变程度的鱼眼图像，验证本文算法的适用性，如图 4~图 6 所示。可以看出，本文算法对于基于多项式畸变模型以及等距投影畸变模型的鱼眼镜头所引入的各种程度的畸变都具有较好的校正效果。校正后的图像线条明晰，
边缘部分没有明显的突兀区域，整体视觉效果良好。

在这里插入图片描述