1. 一阶RC低通滤波器的连续域数学模型

1.1 数学模型的推导

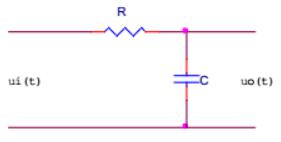
上图是RC低通滤波器的电路模型，根据基尔霍夫定律可知

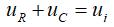
即：

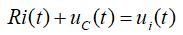
根据电容的特性可知：

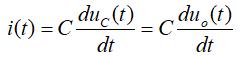
零状态条件下的时域响应可表示为：

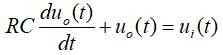
定义时间常数τ=RC，对上述微分方程进行拉氏变换，可得：

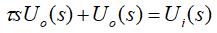
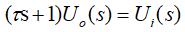
由此可得传递函数：

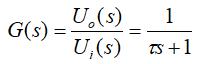
即频域数学模型为：

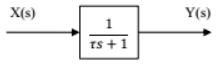
1.2 频率特性

相频特性：

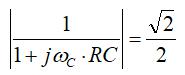
幅频特性：

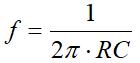
以R=100Ω，C=100nF为例，该低通滤波器的频率特性如下：

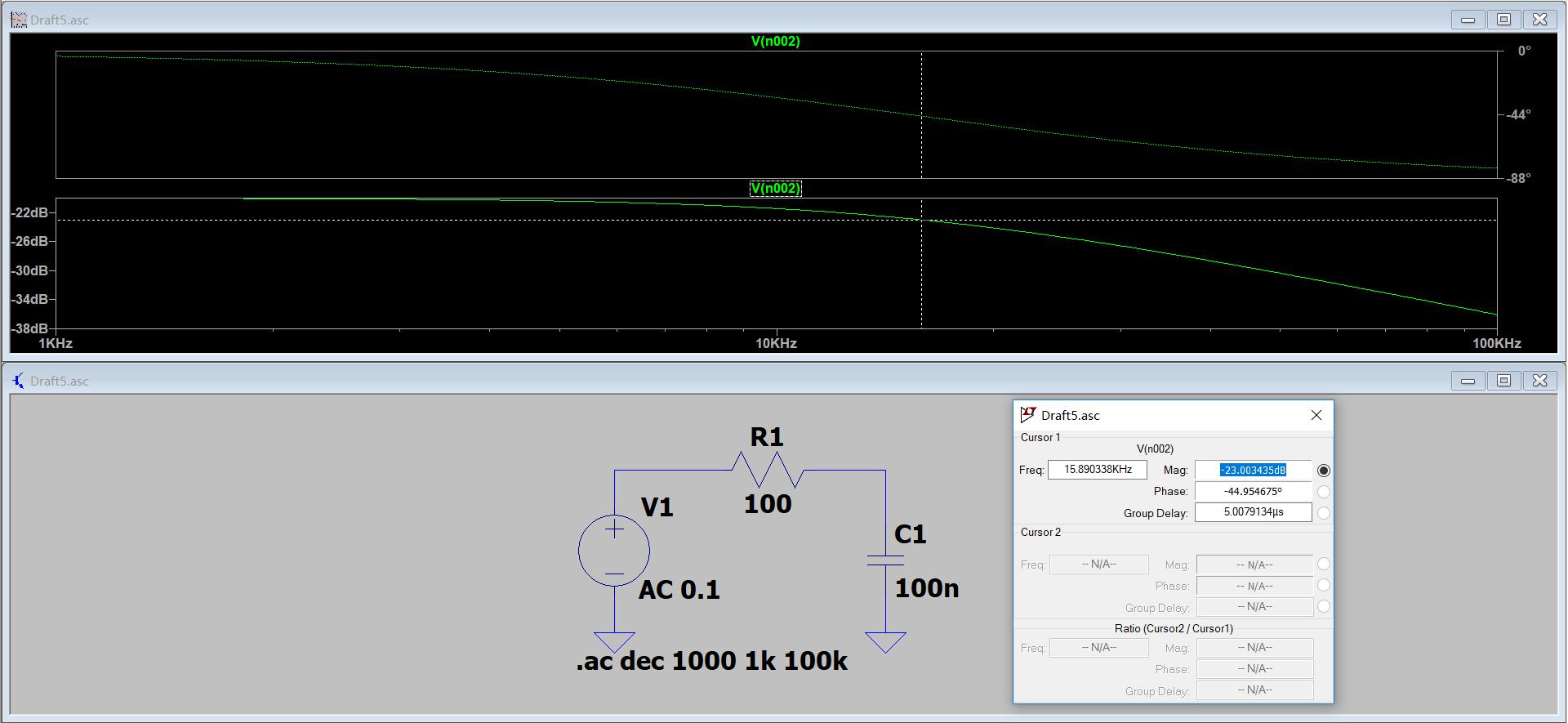
1.3 物理作用

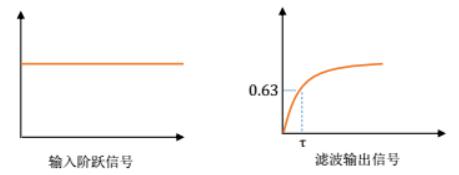
输入一个阶跃信号，经过时间τ之后，输出大约为阶跃量的63%，滞后作用。

2. 一阶RC低通滤波器的算法推导

2.1 离散化

采用一阶后向差分法将传递函数G(s)从S域转化到Z域，其中一阶后向差分中S域与Z域的变化关系是：$$s=\frac{1-z^{-1}}{T}$$其中T是采样周期，带入传递函数G(s)中得：$$G(z)=\frac{Y(z)}{X(z)}=\frac{1}{RC\frac{1-z^{-1}}{T}+1}=\frac{T}{RC(1-z^{-1})+T}$$$$X(z)=Y(z)\cdot \frac{RC(1-z^{-1})+T}{T}$$$$X(z)=\frac{RC}{T}Y(z)-\frac{RC}{T}Y(z)\cdot z^{-1}+Y(z)$$$$X(z)=\frac{RC}{T}Y(z)+Y(z)-\frac{RC}{T}Y(z)\cdot z^{-1}$$Z反变换求差分方程后可得：$$X(n)=(1+\frac{RC}{T})Y(n)-\frac{RC}{T}Y(n-1)$$$$Y(n)=\frac{1}{1+\frac{RC}{T}}X(n)+\frac{\frac{RC}{T}}{1+\frac{RC}{T}}X(n-1)$$令$$A=\frac{T}{RC+T}$$可得$$Y(n)=A\cdot X(n)+(1-A)Y(n-1)$$

2.2 滤波系数

关于滤波系数A，根据幅频特性$$f=\frac{1}{2\pi \cdot RC}$$所以$$RC=\frac{1}{2\pi \cdot f}$$代入$$A=\frac{T}{RC+T}$$可以得到滤波系数A与截止频率f的关系：$$A=\frac{T}{\frac{1}{2\pi \cdot f}+T}=\frac{1}{1+\frac{1}{2\pi \cdot Tf}}$$

3. 一阶RC低通滤波器的C语言实现

#define a 0.01               // 滤波系数a（0-1） 
	
static float oldOutData = 0; //上一次滤波值
	
char filter(void)
{
	nowData  = get_Data();  //本次滤波值
	nowOutData = a * nowData  + (1.0f - a) * oldOutData;
	oldOutData = nowOutData;
	return nowOutData;  
}

4. 缺点及改善方法

4.1 缺点

• 仍然存在灵敏度与平稳度之间的矛盾；
• 小数舍弃带来的误差（单片机很少采用浮点数，小数位要么舍弃，要么四舍五入）。

4.2 改善方法——动态调整滤波系数

4.2.1 实现功能

• 当数据快速变化时，滤波结果能及时跟进，并且数据的变化越快，灵敏度应该越高（灵敏度优先原则）；
• 当数据趋于稳定，并在一个范围内振荡时，滤波结果能趋于平稳（平稳度优先原则）；
• 当数据稳定后，滤波结果能逼近并最终等于采样数据（消除因计算中小数带来的误差）。

4.2.2 调整前判断

• 数据变化方向是否为同一个方向（如当连续两次的采样值都比其上次滤波结果大时，视为变化方向一致，否则视为不一致）；
• 数据变化是否较快（主要是判断采样值和上一次滤波结果之间的差值）。

4.2.3 调整原则

• 当两次数据变化不一致时，说明有抖动，将滤波系数清零，忽略本次新采样值；
• 当数据持续向一个方向变化时，逐渐提高滤波系数，提供本次采样值得权；
• 当数据变化较快（差值＞消抖计数加速反应阈值）时，要加速提高滤波系数。

最后

以上就是单身麦片为你收集整理的一阶RC低通滤波器的数学模型及算法实现1. 一阶RC低通滤波器的连续域数学模型2. 一阶RC低通滤波器的算法推导3. 一阶RC低通滤波器的C语言实现4. 缺点及改善方法的全部内容，希望文章能够帮你解决一阶RC低通滤波器的数学模型及算法实现1. 一阶RC低通滤波器的连续域数学模型2. 一阶RC低通滤波器的算法推导3. 一阶RC低通滤波器的C语言实现4. 缺点及改善方法所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。