一阶低通滤波
低通滤波(Low-pass filter) 是一种过滤方式,规则为低频信号能正常通过,而超过设定临界值的高频信号则被阻隔、减弱,一阶低通滤波的传递函数如下所示。
G
(
s
)
=
ω
c
/
(
s
+
ω
c
)
G(s)=ω_c/(s+ω_c )
G(s)=ωc/(s+ωc)
ω
c
ω_c
ωc为滤波截止角频率,实际应用中经常令
T
=
1
/
ω
c
T=1/ω_c
T=1/ωc,一阶低通滤波器传递函数可改写为:
G
(
s
)
=
1
/
(
T
s
+
1
)
G(s)=1/(Ts+1)
G(s)=1/(Ts+1)
其中T是滤波时间常数,s为拉普拉斯的算子,一阶低通滤波器的伯德图如下所示。
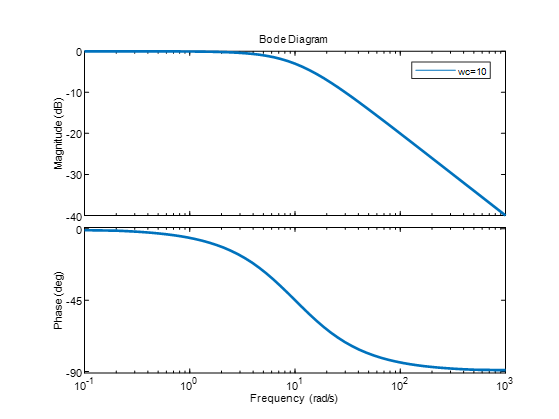
横坐标为,输出与输入之比再取对数。对低通滤波器进行离散化,使用后向差分变换,变换公式为:
s
=
(
1
−
z
−
1
)
/
T
s
s=(1-z^-1 )/T_s
s=(1−z−1)/Ts
将变化公式带入传递函数,可得差分方程:
y
(
n
)
=
(
ω
c
T
s
)
/
(
1
+
ω
c
T
s
)
x
(
n
)
+
1
/
(
1
+
ω
c
T
s
)
y
(
n
−
1
)
y(n)=(ω_c T_s)/(1+ω_c T_s ) x(n)+1/(1+ω_c T_s ) y(n-1)
y(n)=(ωcTs)/(1+ωcTs)x(n)+1/(1+ωcTs)y(n−1)
令
a
=
(
ω
c
T
s
)
/
(
1
+
ω
c
T
s
)
a=(ω_c T_s)/(1+ω_c T_s )
a=(ωcTs)/(1+ωcTs),则
1
/
(
1
+
ω
c
T
s
)
=
1
−
a
1/(1+ω_c T_s )=1-a
1/(1+ωcTs)=1−a,整理后得到低通滤波器的差分方程为:
y
(
n
)
=
a
x
(
n
)
+
(
1
−
a
)
y
(
n
−
1
)
y(n)=ax(n)+(1-a)y(n-1)
y(n)=ax(n)+(1−a)y(n−1)
其中:y(n)为本次滤波值,y(n-1)上次滤波值为, x(n)为本次采样值。
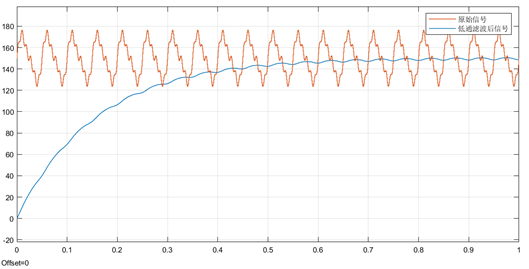
仿真模型
simulink仿真模型
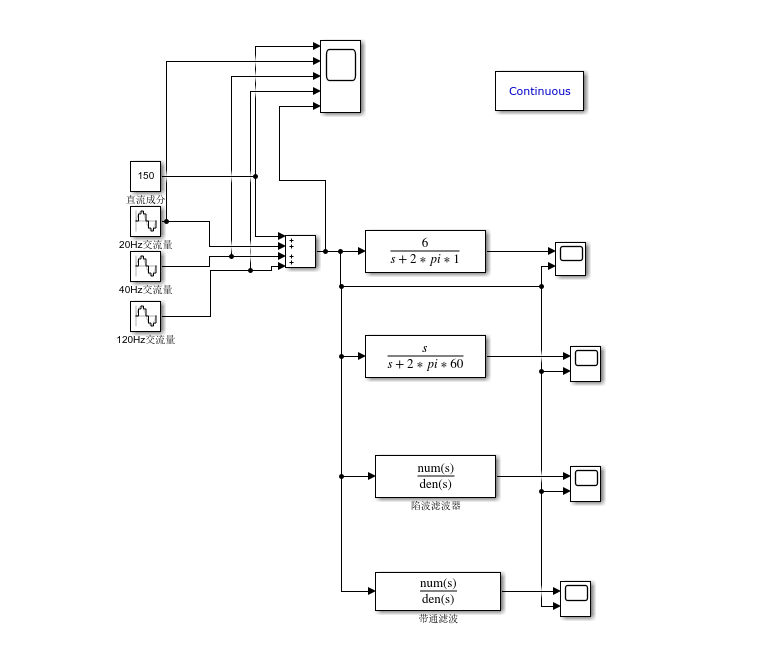
测试信号合成
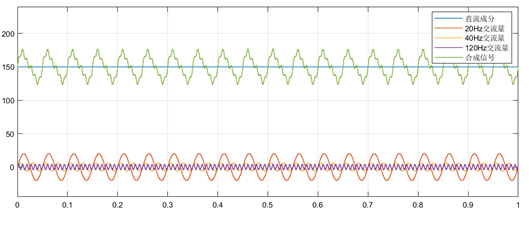
低通滤波截止频率2Hz
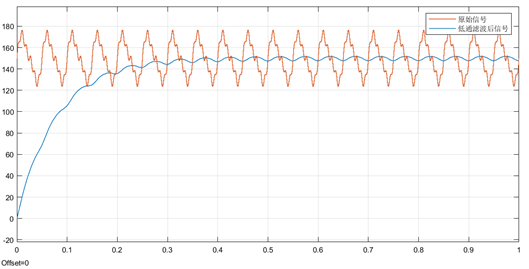
低通滤波截止频率1Hz
最后
以上就是大胆故事最近收集整理的关于一阶低通滤波及其离散化的全部内容,更多相关一阶低通滤波及其离散化内容请搜索靠谱客的其他文章。








发表评论 取消回复