基于Simulink的Ziegler-Nichols PID参数经验整定法

 Ziegler-Nichols整定法适用对象为带纯延迟的一阶惯性环节，即G(s)=K*e^(-τs)/(Ts+1)

其中，K为比例系数；T为惯性时间常数；τ为纯延迟时间常数。

当被控对象的单位阶跃响应曲线看起来近似一条S形曲线时，可用Ziegler-Nichols经验整定公式。

下图(1)为被控对象的阶跃响应曲线中比例系数、惯性常数、纯延迟时间常数

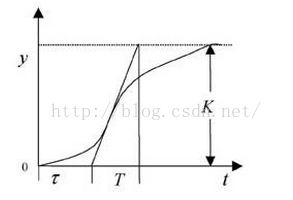
(1)

下表(2)为PID参数的Ziegler-Nichols经验整定公式：

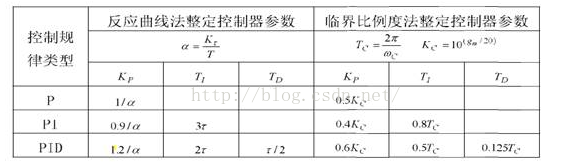
(2)

对于G(s)=25/(s^2+7s+25)，采用Ziegler-Nichols进行PID参数经验整定，步骤如下：

（1）求被控对象的单位阶跃响应，观察阶跃响应曲线是否可以近似为一条S形曲线，如果可以近似为S形曲线则能够采用Ziegler-Nichols进行参数整定，否则无法使用该方法。下图(3)为G(s)=25/(s^2+7s+25)的单位阶跃响应：

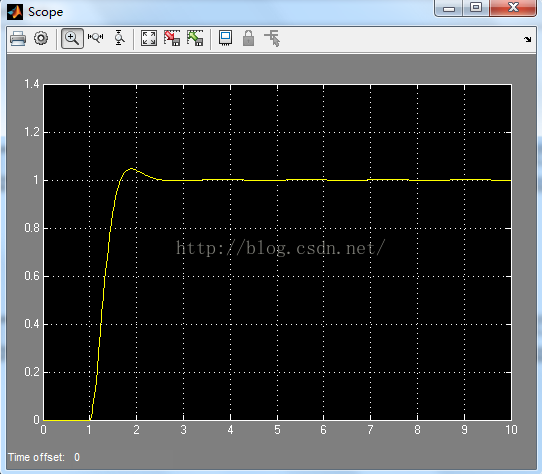
(3)

由此可知，该阶跃响应曲线近似S形曲线。因此，对于G(s)=25/(s^2+7s+25)，可以采用Ziegler-Nichols PID参数经验整定法。

（2） 根据被控对象阶跃响应，求取比例系数K、惯性常数T及纯时间延迟常数τ：

对于比例系数K，它为被控对象阶跃响应稳定后的幅值，本例中可知K=1；

对于惯性常数T及纯时间延迟常数τ则需要根据图(1)所示各自的含义求取，纯时间延迟常数τ即为曲线的拐点的切线在X轴上的交点，惯性常数T即为曲线的拐点处的切线在幅值为K时对应的X轴的坐标减去纯时间延迟常数τ，在本例中可得到T=0.506，τ=0.065;

（3） 根据经验整定公式表求取PID初始参数KP、KI、KD：

KP=1.2*T/(K*τ)=9.34   KI=2*τ=0.13  KD=0.5*τ=0.0325

（4） 搭建simulink模块构建该模型如图(4）所示；

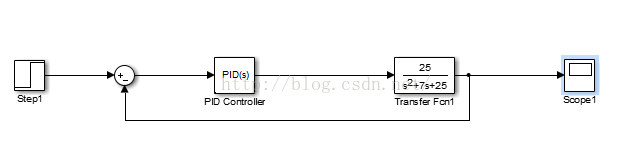
(4)

（5）       仿真所建模型，得到PID控制后的输出如图(5)所示；

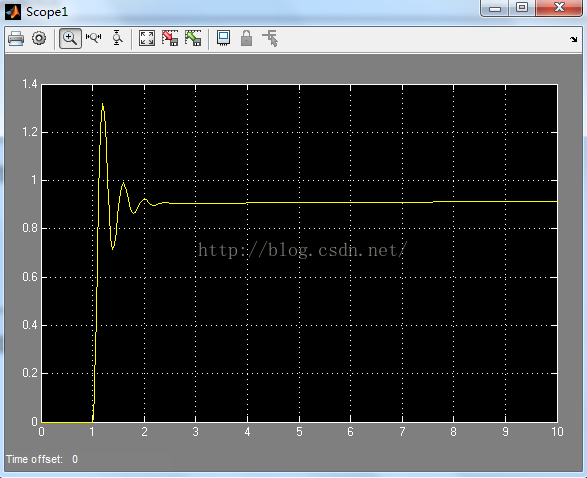
(5)

可以看出，在1-2s时输出存在振荡，后面趋向稳定。