概述
本文部分素材来自Rick Hill的网络教程System Dynamics and Control第10和第11节，请支持原作者。
https://www.youtube.com/watch?v=h73CudC0FQo&list=PL4VMBEQr3gMG7x97VfO8skq2k-52GCTMZ&index=2www.youtube.com一阶系统的基本性质
一阶系统的标准形式（canonical form）：
一阶系统的传递函数 TF：
关键参数：
一阶系统的阶跃响应（时域分析）
对于传递函数为
的一阶系统，当输入型号为阶跃函数
时，
其时域表达式为
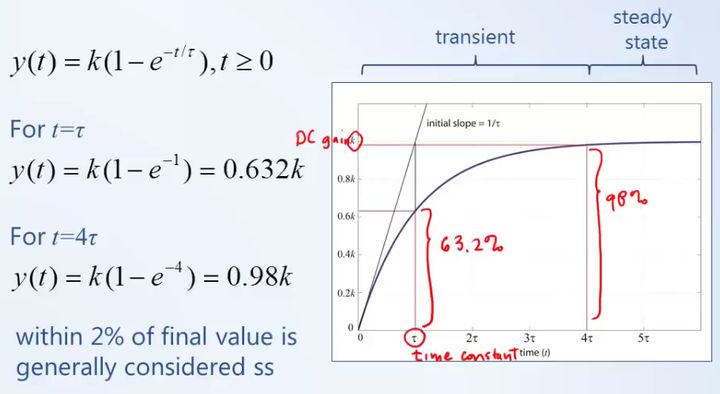
通过观察一阶系统输出信号的
二阶系统的基本性质
二阶系统的标准形式（canonical form）：
二阶系统的传递函数 TF：
关键参数：
极点是使传递函数趋于无穷的s，根据
可得
极点=
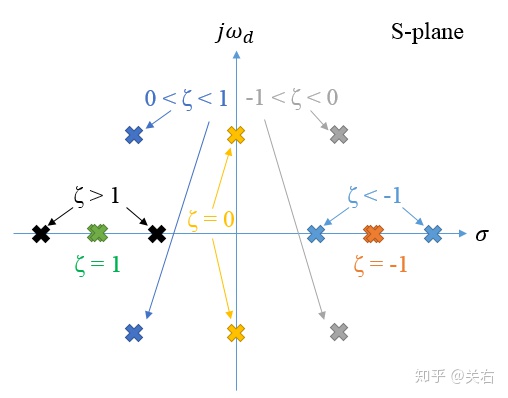
二阶系统极点包含实部与虚部两部分，
二阶系统稳定（无论是渐近稳定或是BIBO稳定）的前提是极点都位于负（左）半平面。
对于极点分布在左半平面的情况（
另外，自然频率
另外有
二阶系统的欠阻尼阶跃响应（时域分析）
对于传递函数为
的二阶系统，当输入型号为阶跃函数
时。
其时域表达式为
定义：
2%稳定时间
峰值时间
超调量
由此可见极点位置对于波形的影响，同样的，根据
编辑于 2019-03-12
最后
以上就是落后大雁为你收集整理的一阶系统单位阶跃响应的特点_控制理论学习笔记（4）——一阶系统和二阶系统...的全部内容，希望文章能够帮你解决一阶系统单位阶跃响应的特点_控制理论学习笔记（4）——一阶系统和二阶系统...所遇到的程序开发问题。
如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。
本图文内容来源于网友提供，作为学习参考使用，或来自网络收集整理，版权属于原作者所有。
发表评论 取消回复