一阶RC低通滤波器的离散化

前面我们讲了一阶系统传函的标准形式和时域响应。今天说下生活中对应的一个一阶系统——一阶RC低通滤波器。

1、典型电路

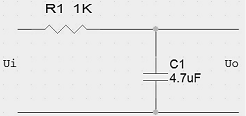
1.1时域下

电容的电流：

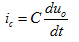
基尔霍夫电压定律得：

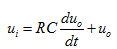
$u_i$的单位是V，时间常数$\tau$ =RC； 解微分方程得：

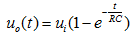
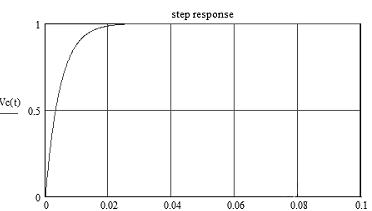
看下时域下的响应曲线：

假设电容初始电压值为0 ，R=1K，C=4.7uF ，ui=1V ，T=RC 那么V(τ)=0.632 V。

1.2 频域下

再变化下：

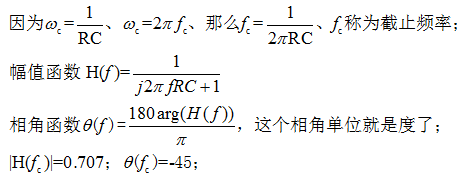
看下幅频和相频特性曲线：


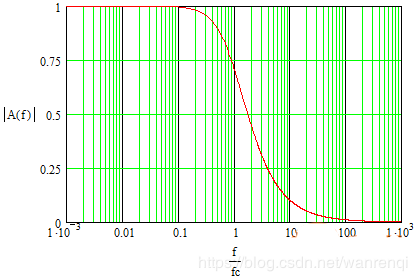
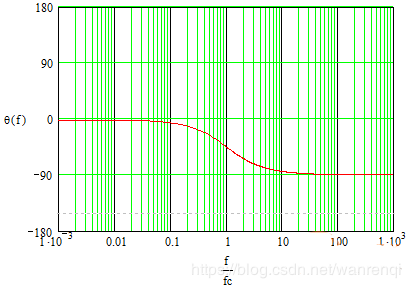
幅频特性图的对数表示：

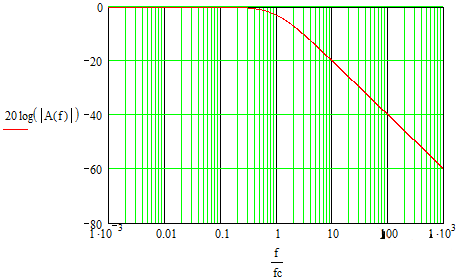
由上可以看出：

1. 当ω<ωc时，幅值是平行于坐标的直线，基本无衰减；
2. 当ω>>ωc时，是斜率与-20dB/十倍频成比例的一条直线；
3. 当ω=ωc时，增益衰减至0.707，即-3dB，相位滞后45度，对应低通滤波器，该频率通常被称为截止频率

当使用一个一阶RC低通滤波器的时候，如果信号频率等于截止频率的时候，有个45°的延迟，就会涉及到相角的补偿。

2、RC低通滤波器的离散化

对上面的微分方程拉氏变换得：

再通过z变换（方法很多，如一阶前向差分、双线性变换等，这里用一阶后向差分法）

3、一阶低通数字滤波器的验证

实验图形如下：

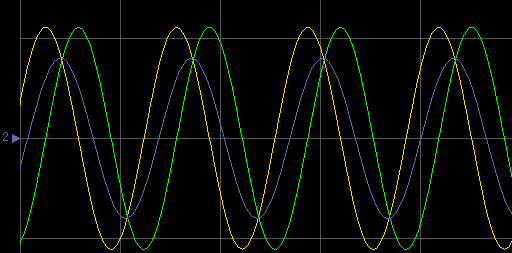
图中黄色波形为输入a，绿色为信号b，紫色为一阶低通滤波器的输出信号c，由图可见，输
出信号滞后输入信号45度，幅值为输入信号的0.707倍。

当我们知道输入信号的频率时，我们可以做个自适应滤波，根据输入信号的频率变化来动态
改变滤波器的截止频率。这样我们就可以知道滤波器的输出相位时钟和输入信号相差45度。

注：内容由 (https://blog.csdn.net/qq_27334499/article/details/52186336?depth_1-utm_source=distribute.pc_relevant.none-task-blog-BlogCommendFromMachineLearnPai2-1&utm_source=distribute.pc_relevant.none-task-blog-BlogCommendFromMachineLearnPai2-1
整理而来。

最后

以上就是无限小馒头最近收集整理的关于一阶RC低通滤波器的离散化的全部内容，更多相关一阶RC低通滤波器内容请搜索靠谱客的其他文章。