概述
软件编程中用到的数学是离散化的，而物理世界是连续的。把物理世界中连续性的方程表达式，转换成软件世界中离散形式是必须的。控制论中最重要的就是有关拉普拉斯变换的传递函数，只有把它变成离散形式（Z变换），这样才能用于编程（模拟实现）。下面打算一般形式的普拉斯变换的传递函数变成Z变换形式的数学原理做一下解释：（非本专业的人员可能看不懂，基本内容可以参考教材《自动控制原理（胡寿松版）》，好像教材中并没给出详细证明过程，决定补充一下这个证明过程）。
拉普拉斯变换与Z变换的关系（一）
题目1 证明如果连续函数f(t)的任意拉普拉斯变换为F(s),而且其的全部极点pi已知，则f(t)的Z变换F(z)为下式：
解：
存在下面公式
（公式1）
对于信号采样，有下面公式
从而
或
（公式2）
根据公式1，有：
代入公式2得到：
（公式3）
<注：公式3中的z只与采样有关,而与积分时使用的s无关>
定义
则：
（公式4）
对公式4两边同时乘上
得到：
（公式5）
公式4减去公式5得到
（公式 6）
将公式6代入公式3得到
证明上式用到闭曲线
，
为直线段
,
：
R充分大的时候，
。
证明完毕。
另：对留数的计算（极点
是m阶重极点）
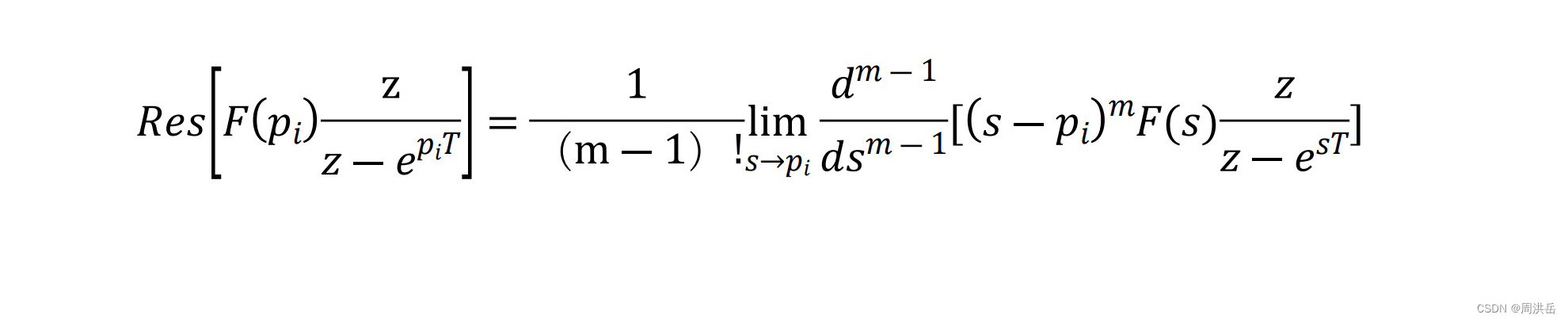
最后
以上就是深情大炮为你收集整理的关于传递函数的离散化的全部内容，希望文章能够帮你解决关于传递函数的离散化所遇到的程序开发问题。
如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。
本图文内容来源于网友提供，作为学习参考使用，或来自网络收集整理，版权属于原作者所有。
发表评论 取消回复