传递函数的离散化0. 在matlab中的概括1.离散化方法12. 离散化理论推导3. 离散化代码4. 例子

75 阅读 0 评论 50 点赞

我是靠谱客的博主热情云朵，最近开发中收集的这篇文章主要介绍传递函数的离散化0. 在matlab中的概括1.离散化方法12. 离散化理论推导3. 离散化代码4. 例子，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

0. 在matlab中的概括
1.离散化方法[^1]
2. 离散化理论推导
3. 离散化代码
- 3.1 最简单的离散化：c2d（T）[^2]
- 3.2 z离散化：c2d（ 'z'）[^3]
- 3.3 PID离散化：c2d（'tustin'）[^1]
- 3.4 PR离散化：c2d（'tustin'）[^1]
- 3.5 进行传递函数的计算：以陷波器为例[^4]
4. 例子

0. 在matlab中的概括

形式	模块建模类型	求解器类型
block模块	连续	连续
$s$ 函数：`Transfer Fcn`模块	连续	连续
$z$ 函数：`Discrete Transfer Fcn`模块	离散	离散
m语言：`MATLAB Function`模块	离散	连续

1.离散化方法¹

离散方法	s到z的替代关系
Zero-order hold	$X(z)=(1-z^{-1})z left { L^{-1}left {frac{X(s)}{s}right }right }$
Firs-order hold	$X(z)=frac{(z-1)^2}{zT_s}z left { L^{-1}left {frac{X(s)}{s}right }right }$
Forward Euler	$s=frac{z-1}{T_s}$
Backward Euler	$s=frac{z-1}{zT_s}$
Trapezoid(Tustin)	$s=frac{2}{T_s} frac{z-1}{z+1}$
Tustin with pre-warping	$omega_{0}}{tan(omega_0 Omega}$ 未完待续

在这里插入图片描述
其中离散化的方法又有很多：前向差分；后向差分；tustin；零极点匹配；脉冲响应；阶跃响应；

https://blog.csdn.net/weixin_35131453/article/details/115993833 (离散分类)
Matlab-Simulink_离散模块：https://blog.csdn.net/qq_41955225/article/details/122828438

z到s的变换：
command使用方式是：
sysc = d2c(sysd,method)
默认方式是zoh；

H = tf([1 -1],[1 1 0.3],0.1);
Hc = d2c(H)

输出：
在这里插入图片描述
需要注意 ：离散的步长、simulink中仿真的步长、离散正弦波的步长、以及powergui的离散步长，这三种步长有什么区别？？？

2. 离散化理论推导

如何将连续域的控制器进行离散化实现：（使用的欧拉法和塔斯汀法）https://zhuanlan.zhihu.com/p/20927674
【计算机控制|Python|Matlab】传递函数离散化：（使用欧拉法推导）https://zhuanlan.zhihu.com/p/366422414

积分的离散：
$积分值 + = 采样值 * d T$
https://blog.csdn.net/weixin_43455581/article/details/109220419

3. 离散化代码

从某个连续传递函数得到在特定采样周期下的离散函数

3.1 最简单的离散化：c2d（T）²

num = 0.6321;           % 分子多项式的系数
den = [1, -0.3679];     % 分母多项式的系数
T   = 1;                % 采样周期（1s）
Gz = tf(num, den, T)    % 离散传递函数
Gs = d2c(Gz)            % 连续传递函数

3.2 z离散化：c2d（ ‘z’）³

% transfor function
sys = tf([1 -1], [1 4 5]);
% discretize
ts = 0.1; % 采样周期
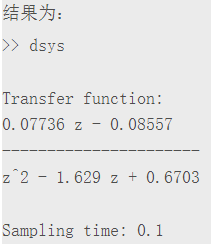
dsys = c2d(sys, ts, 'z'); % 转化为差分方程
% extract
[num, den] = tfdata(dsys,'v'); % 提取差分方程系数

在这里插入图片描述

3.3 PID离散化：c2d（‘tustin’）¹

 Kp=1;Ki=2;Kd=3;Ts=1e-3;
PID=tf([Kd,Kp,Ki],[1,0])
c2d(PID,1e-3,'tustin')

可得到：
在这里插入图片描述
和计算结果一致。
同时Matlab的c2d()函数总共支持五种离散方法。

 
    SYSD = C2D(SYSC,TS,METHOD) computes a discrete-time model SYSD with 
    sampling time TS that approximates the continuous-time model SYSC.
    The string METHOD selects the discretization method among the following:
       'zoh'       Zero-order hold on the inputs
       'foh'       Linear interpolation of inputs
       'impulse'   Impulse-invariant discretization
       'tustin'    Bilinear (Tustin) approximation.
       'matched'   Matched pole-zero method (for SISO systems only).
    The default is 'zoh' when METHOD is omitted.

3.4 PR离散化：c2d（‘tustin’）¹

Kp=1;
Kr=10;
wc=2*pi*5;
wo=2*pi*50;
PRs=Kp+tf([2*Kr*wc,0],[1,2*wc,wo^2])
PRz = c2d(PRs,1e-3,'tustin')

命令行输出：
在这里插入图片描述
可得到，离散化后，数字实现的C语言为：
y_k - 1.847y_k1 + 0.9405y_k2 = 1.297u_k - 1.847u_k1 +0.643*u_k2;
即
y_k = 1.297*u_k - 1.847*u_k1 +0.643*u_k2 + 1.847*y_k1 - 0.9405*y_k2 ;

https://blog.csdn.net/xstx1996/article/details/92723025

3.5 进行传递函数的计算：以陷波器为例⁴

首先，陷波器的传递函数是：
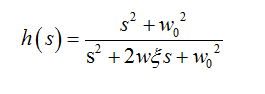
在这里插入图片描述
利用matlab对其进行离散化，tustin变换：

syms w0  s Ts z xi   % 定义符号变量
G1 =(s^2+w0^2)/(s^2+2*w0*xi*s+w0^2)         %传递函数
sys_s2c = 2*(z-1)/Ts/(z+1)
G2 = subs(G1,s,sys_s2c)    %离散化  tustin变换
G3 = collect(G2,z)  % 将表达式G2中的以z为变量合并相同次幂；

参考文献里还有陷波器的离散化、系数计算等等

https://blog.csdn.net/arris1992/article/details/81013519
https://blog.csdn.net/qq_34473360/article/details/103172281
死磕陷波器：https://blog.csdn.net/xklzw/article/details/113181680
MATLAB function的使用方法：https://blog.csdn.net/xklzw/article/details/113181680

C语言的形式：

VARIABLE 2ND ORDER NOTCH IIR FILTER: https://www.dsprelated.com/showcode/173.php
https://dsp.stackexchange.com/questions/11290/linear-phase-notch-filter-band-reject-filter-implementation-in-c
http://dspguide.com/ch19/3.htm

另外一个例子：⁵

syms wr w0 Kp Kr s Ts z % 定义符号变量
G1 =2*Kr*wi*s/(s^2+2*wi*s+w0^2) %R控制
G2 = subs(G1,s,2*(z-1)/Ts/(z+1)) %离散化 tustin变换
G3 = collect(G2,z) % 将表达式G2中的以z为变量合并相同次幂；

转换出来就是：
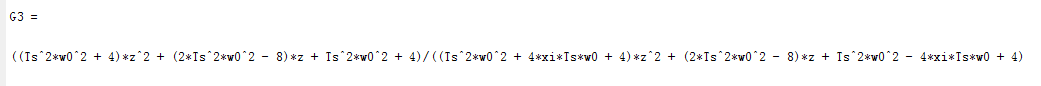
在这里插入图片描述
和之前师兄发的一致。

4. 例子

2022年9月29日
1、https://zhuanlan.zhihu.com/p/340449640（C语言如何实现积分和微分，以及3个步长的关系）
2、https://blog.csdn.net/wanrenqi/article/details/111566934（专栏的3篇文章）
s函数：下图，注意延迟90°在simulink里是弧度的。
solver选择为定步长：1e-6
传递函数为：
$G_s(s)=frac{ 1.013*10^{-5}s^2 + 3.183*10^{-06} s + 1}{1.013*10^{-05} s^2 + 0.003183 s + 1}$

clc
clear

wc=2*pi*50;
m1=5e-4;
m2=0.5;

num=[1/(wc^2) 2*m1/wc 1];
den=[1/(wc^2) 2*m2/wc 1];
sys=tf(num,den);

Ts=1e-3;
dsys=c2d(sys,Ts,'tustin') %下一步离散为z的时候使用

在这里插入图片描述
z函数：

首先是离散的，因此solver需要设置为离散的，仿真步长可以设置为变步长；
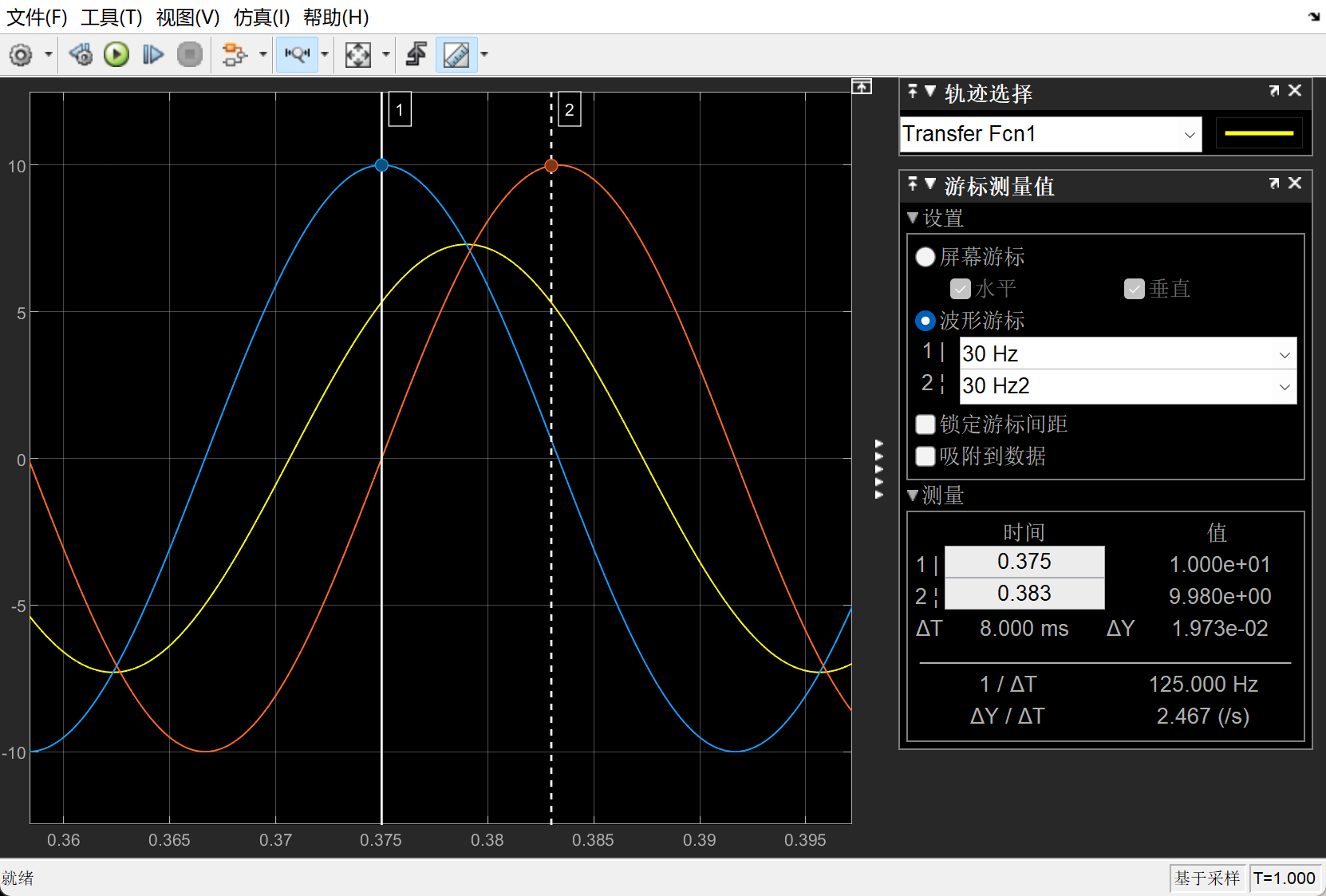
sine wave的模块采样时间需要和s函数替换到z函数时的离散周期一致，否则最后结果将是错误的。
Z函数为：
$z^2 - 1.651 z + 0.8669}{z^2 - 1.651 z + 0.7342}$
Ts=1e-3
错误的图和正确的图分别为：

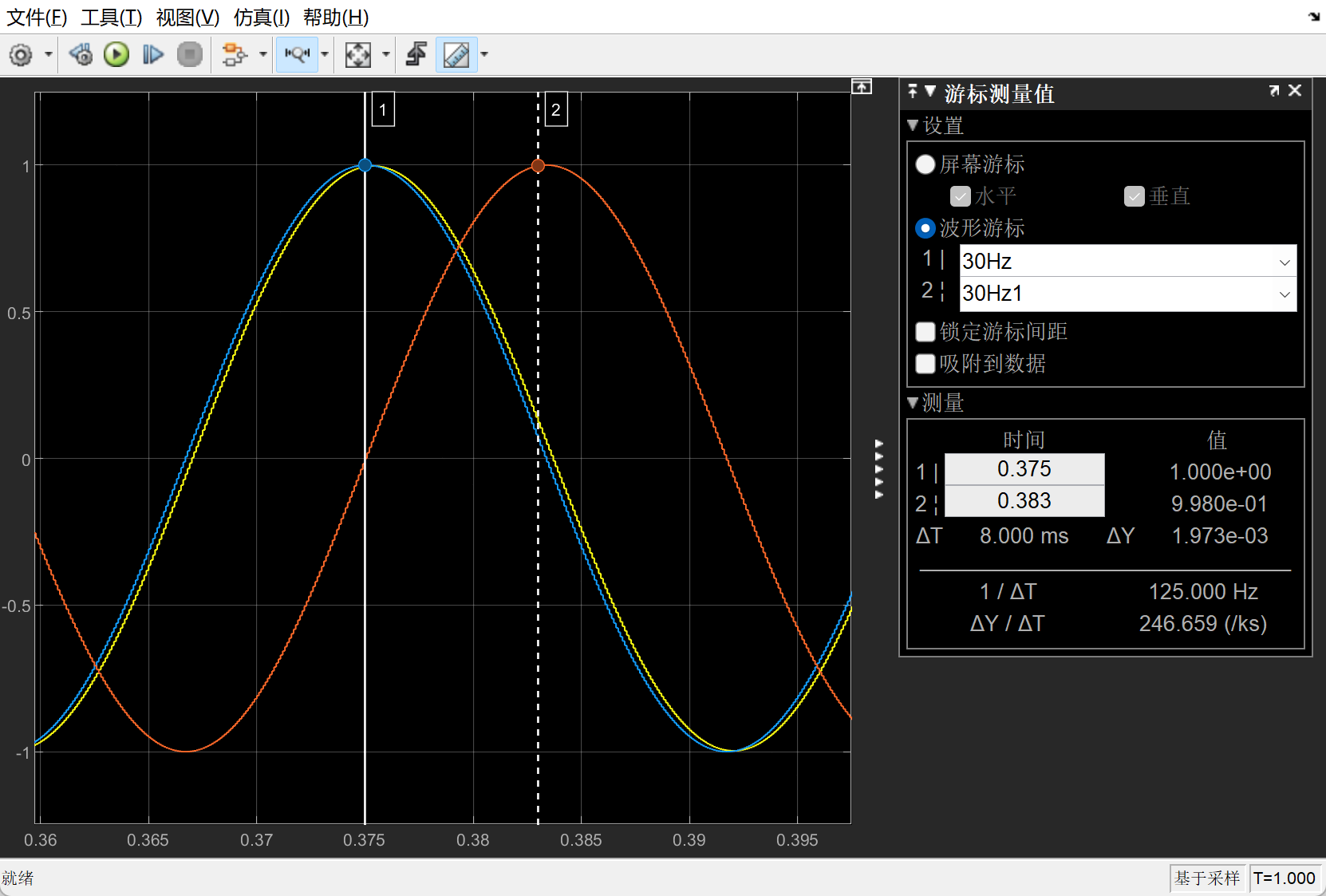
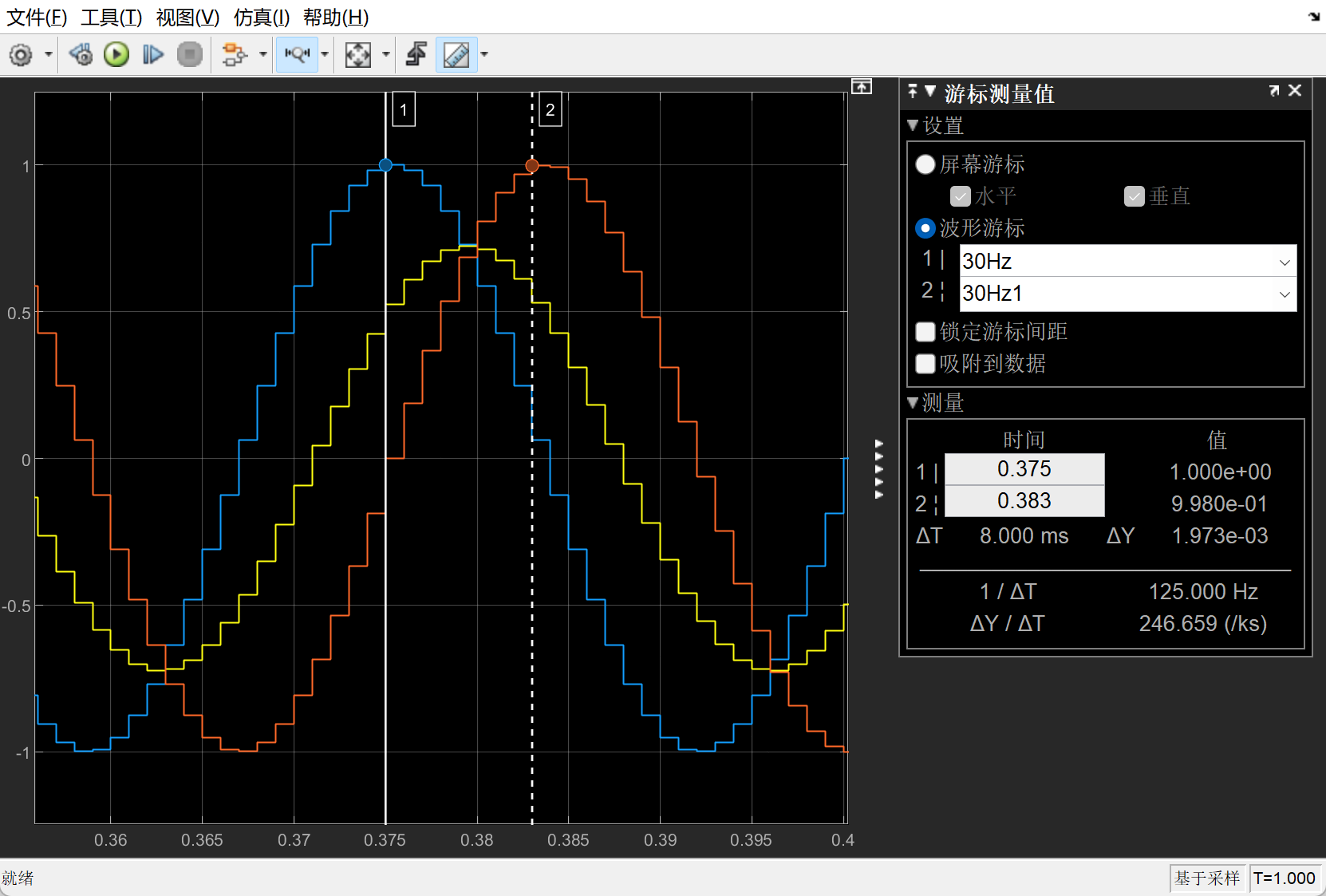
仿真图为：（此处不需要powergui，powergui是需要电气模块时才需要的。）

https://blog.csdn.net/weixin_44162637/article/details/122147328

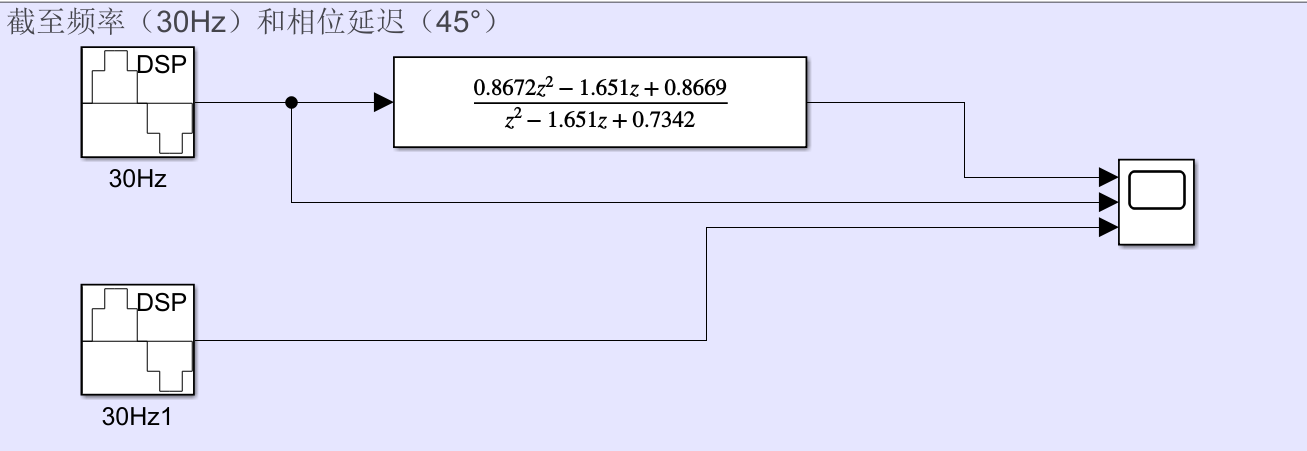
在这里插入图片描述
z变换=>差分方程

首先知道 $Z$ 变换： $F (Z) = Z [f (t)]$ ；
以及实数位移定理中的迟后定理： $Z[x(t−kT_0 )]=Z^{−k} X(z)$

https://www.cxymm.net/article/qq_32515081/117095744#Z函数
https://blog.csdn.net/weixin_36815313/article/details/114822577
https://bbs.huaweicloud.com/blogs/353400

$z^2 - 1.651 z + 0.8669}{z^2 - 1.651 z + 0.7342}$
因此有：
$Y(z)*(z^2 - 1.651 z + 0.7342)={U(z)}*(0.8672 z^2 - 1.651 z + 0.8669)$
根据z变换，有：
$y_{(k+2)}-1.651y_{(k+1)}+ 0.7342y_{(k)}=0.8672x_{(k+2)}- 1.651x_{(k+1)} + 0.8669x_{(k)}$
经过变换得：
$y_{(k+2)}=1.651y_{(k+1)}-0.7342y_{(k)}+0.8672x_{(k+2)}- 1.651x_{(k+1)} + 0.8669x_{(k)}$
也就是：
$y_{(k)}=1.651y_{(k-1)}-0.7342y_{(k-2)}+0.8672x_{(k)}- 1.651x_{(k-1)} + 0.8669x_{(k-2)}$

https://blog.csdn.net/wanrenqi/article/details/111566934

仿真图：
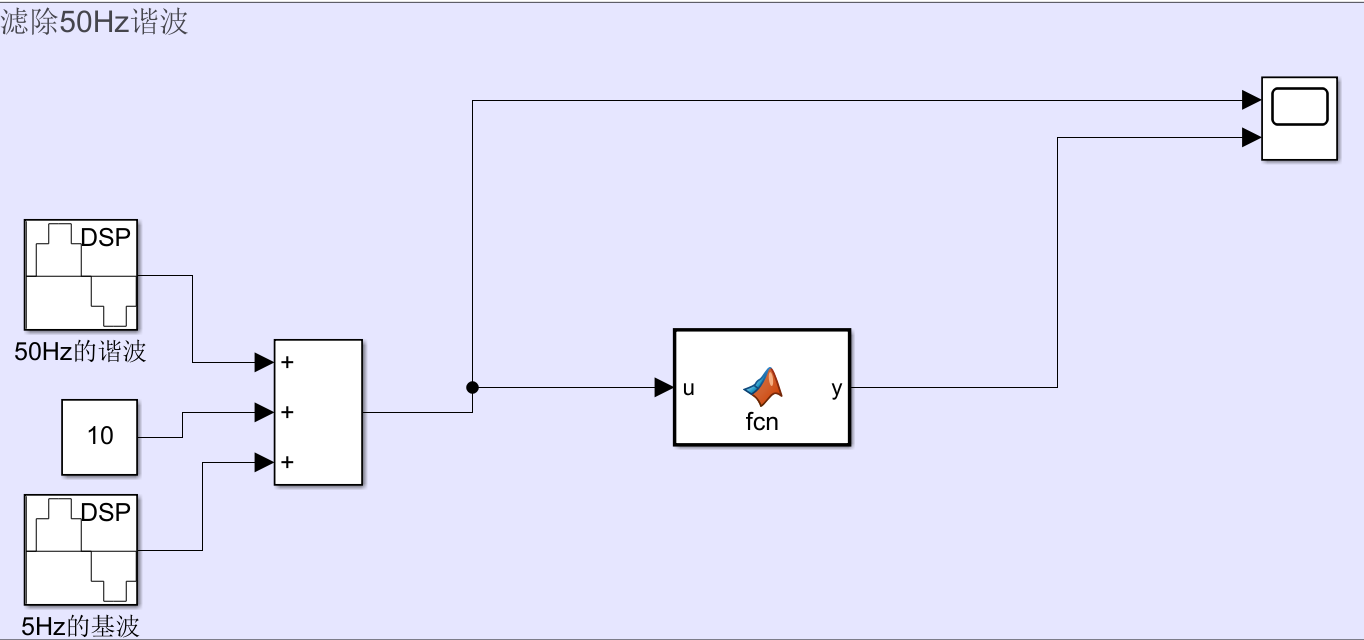
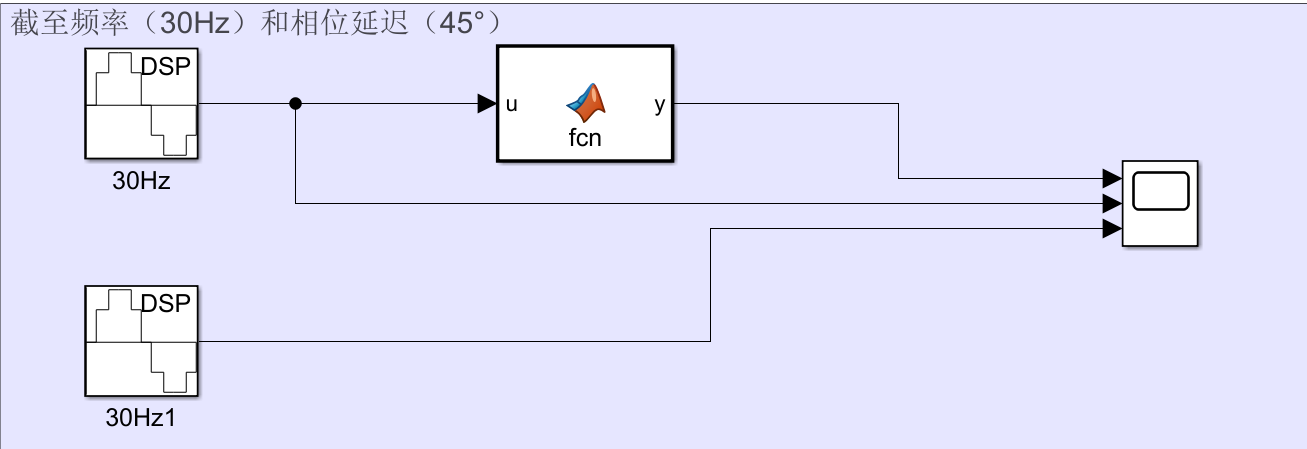
在这里插入图片描述

C语言代码：

function y = fcn(u)

persistent yl;  %定义一个静态变量
if isempty(yl)  %给静态变量赋初值
   yl=0;
end
persistent yll;  %定义一个静态变量
if isempty(yll)  %给静态变量赋初值
   yll=0;
end
persistent ul;
if isempty(ul)
    ul=0;
end
persistent ull;
if isempty(ull)
    ull=0;
end

y=1.651*yl-0.7342*yll+0.8672*u-1.651*ul+0.8669*ull;

yll=yl;
yl=y;
ull=ul;
ul=u;

结果图：
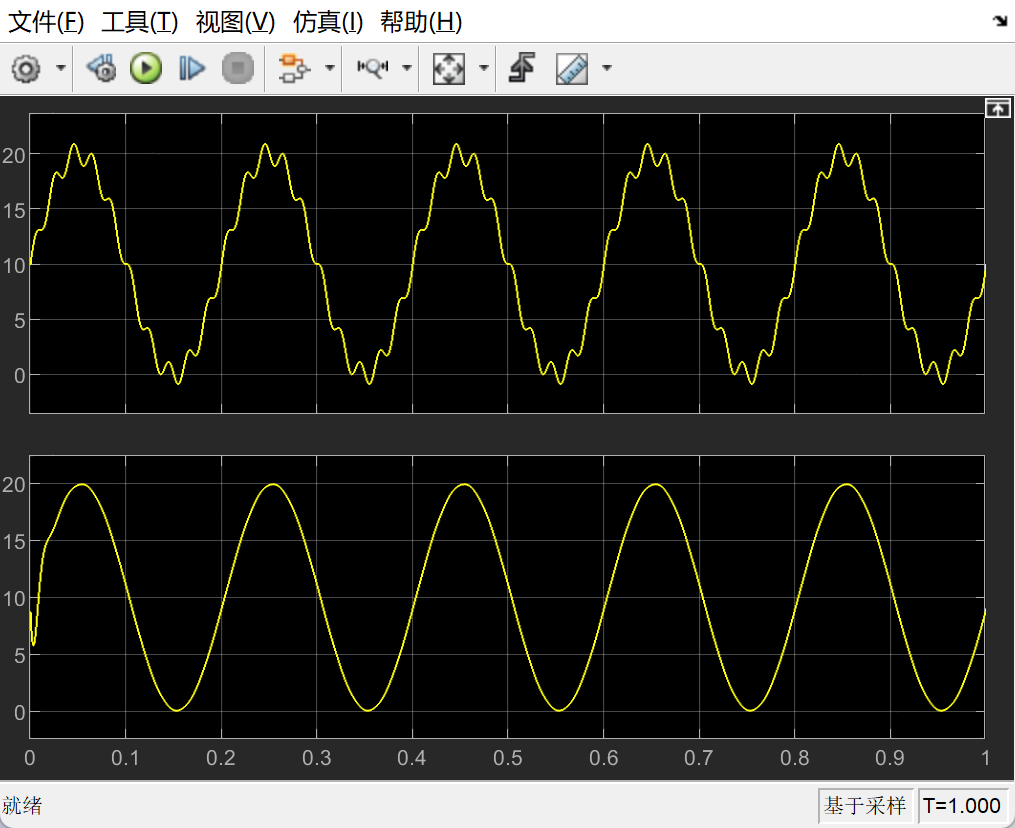
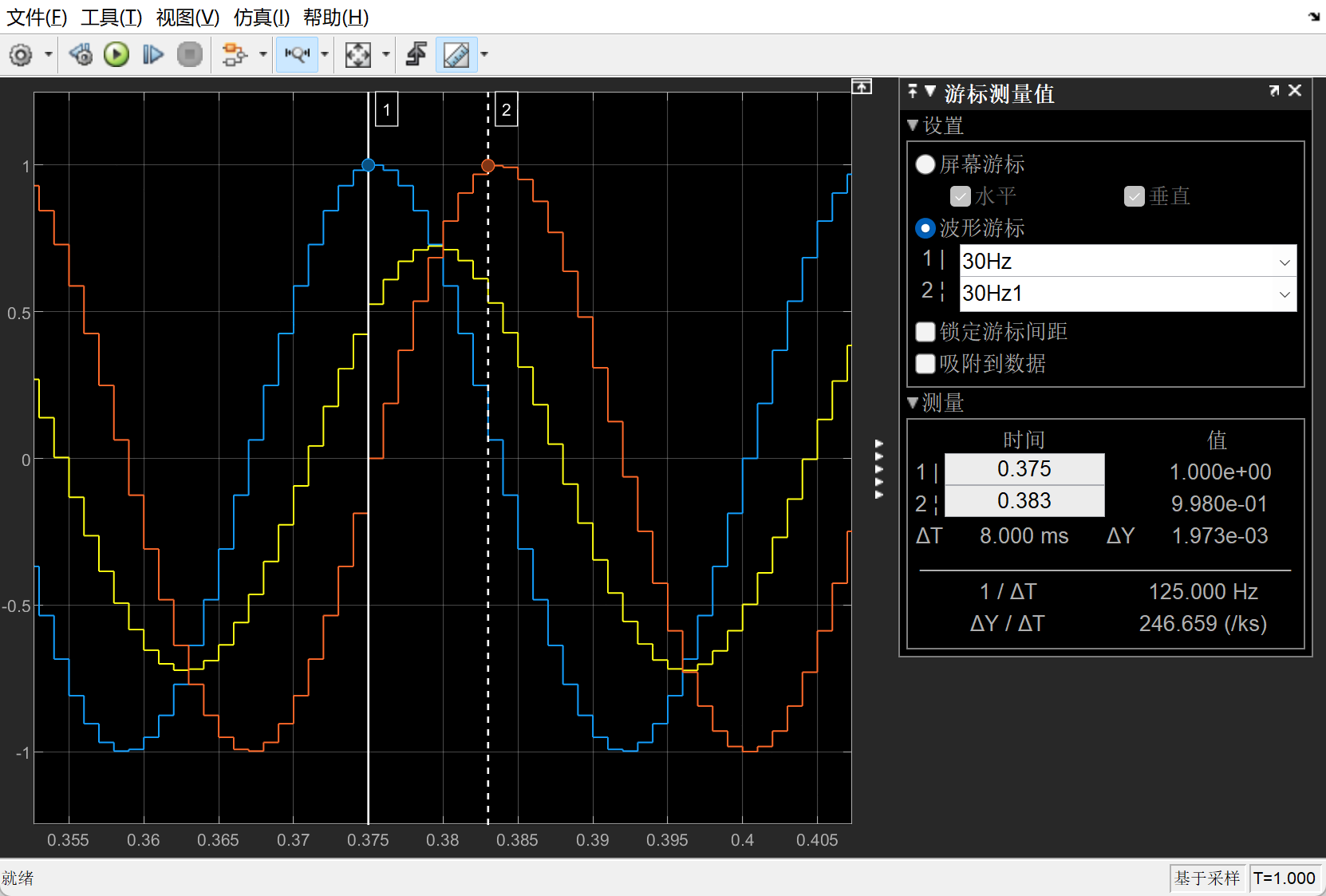
在这里插入图片描述

https://blog.csdn.net/qq_27158179/article/details/82739641 ↩︎ ↩︎ ↩︎
https://blog.csdn.net/xstx1996/article/details/92723025：里面有很多内容，传递函数化简等等 ↩︎
https://blog.csdn.net/ocean_ele/article/details/53442812 ↩︎
https://blog.csdn.net/qq_34473360/article/details/103172281 ↩︎
https://blog.csdn.net/weixin_35131453/article/details/115993833 ↩︎

最后

以上就是热情云朵为你收集整理的传递函数的离散化0. 在matlab中的概括1.离散化方法12. 离散化理论推导3. 离散化代码4. 例子的全部内容，希望文章能够帮你解决传递函数的离散化0. 在matlab中的概括1.离散化方法12. 离散化理论推导3. 离散化代码4. 例子所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。

本图文内容来源于网友提供，作为学习参考使用，或来自网络收集整理，版权属于原作者所有。

本文分类：matlab
浏览次数：75 次浏览
发布日期：2023-05-22 09:25:01
本文链接：https://www.kaopuke.com/article/k-p-k_14_ujocfz_13__7__14_y.html

传递函数的离散化0. 在matlab中的概括1.离散化方法12. 离散化理论推导3. 离散化代码4. 例子

概述

目录

0. 在matlab中的概括

1.离散化方法¹

2. 离散化理论推导

3. 离散化代码

3.1 最简单的离散化：c2d（T）²

3.2 z离散化：c2d（ ‘z’）³

3.3 PID离散化：c2d（‘tustin’）¹

3.4 PR离散化：c2d（‘tustin’）¹

3.5 进行传递函数的计算：以陷波器为例⁴

4. 例子

最后

评论列表共有 0 条评论

发表评论取消回复

传递函数的离散化0. 在matlab中的概括1.离散化方法12. 离散化理论推导3. 离散化代码4. 例子

概述

目录

0. 在matlab中的概括

1.离散化方法1

2. 离散化理论推导

3. 离散化代码

3.1 最简单的离散化：c2d（T）2

3.2 z离散化：c2d（ ‘z’）3

3.3 PID离散化：c2d（‘tustin’）1

3.4 PR离散化：c2d（‘tustin’）1

3.5 进行传递函数的计算：以陷波器为例4

4. 例子

最后

相关文章

评论列表共有 0 条评论

发表评论 取消回复

1.离散化方法¹

3.1 最简单的离散化：c2d（T）²

3.2 z离散化：c2d（ ‘z’）³

3.3 PID离散化：c2d（‘tustin’）¹

3.4 PR离散化：c2d（‘tustin’）¹

3.5 进行传递函数的计算：以陷波器为例⁴

发表评论取消回复