TensorFlow常见函数解析

89 阅读 0 评论 59 点赞

我是靠谱客的博主会撒娇香水，最近开发中收集的这篇文章主要介绍TensorFlow常见函数解析，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

1、tf.slice(input, begin, slice_dimension)

····
import tensorflow as tf
a = tf.constant([[1, 2, 3], [-1, -2, -2], [3, 2, 1]])
sess = tf.InteractiveSession()
b = tf.slice(a, [1, 0], [2, 3])
#[1, 0]表示从矩阵的[1, 0]开始计算截取位置
#注：由于是二维矩阵，所以此时只能填充二维数组
#[2, 3]表示在[1, 0]的基准位置取2行三列元素
sess.run(a)
sess.run(b)
'''
array([[ 1,  2,  2],
   [-1, -2, -3],
   [ 3,  2,  1]])
array([[-1, -2, -3],
   [ 3,  2,  1]])
'''
····

2、tf.reshape(input, shape)

注：shape为待转换的矩阵形状，其参数具体根据输入确定。并且其中有且仅允许存在一个‘-1’，表示在该维度上由计算机得出。并且在shape中的元素值乘积等于输入矩阵个数，且shape中元素的个数为输出数组维度

import tensorflow as tf
a = tf.constant([[1, 2, 3, 4], [4, 3, 2, 1], [1, 3, 5, 6], [1, 2, 3, 5]])
#a为二维数组
b = tf.reshape(a, [1, 2, 2, 4])
c = tf.reshape(a,  [-1, 2])
d = tf.reshape(a, [2, 1, 2, -1])
e = tf.reshape(a, [4, -1, 2, 2])
sess = tf.InteractiveSession()
sess.run(a)
sess.run(b)
sess.run(c)
sess.run(d)
sess.run(e)
'''
运行结果
>>> sess.run(a)
array([[1, 2, 3, 4],
       [4, 3, 2, 1],
       [1, 3, 5, 6],
       [1, 2, 3, 5]])
       #输出原始数据（方括号的数目即为矩阵元素的维度）
>>> sess.run(b)
array([[[[1, 2, 3, 4],
         [4, 3, 2, 1]],

        [[1, 3, 5, 6],
         [1, 2, 3, 5]]]])
         #原始数组输出为2*2矩阵并且进行4列分布的四维矩阵
>>> sess.run(c)
array([[1, 2],
       [3, 4],
       [4, 3],
       [2, 1],
       [1, 3],
       [5, 6],
       [1, 2],
       [3, 5]])
       #原始数组分成两列分布的二维矩阵
>>> sess.run(d)
array([[[[1, 2, 3, 4],
         [4, 3, 2, 1]]],


       [[[1, 3, 5, 6],
         [1, 2, 3, 5]]]])
>>> sess.run(e)
array([[[[1, 2],
         [3, 4]]],


       [[[4, 3],
         [2, 1]]],


       [[[1, 3],
         [5, 6]]],


       [[[1, 2],
         [3, 5]]]])
'''

3、tf.transpose(input, shape)

注：shape[dim1, dim2, …], 当输入shape为2维时，即表示转置[1, 0]； [0, 1]表示保持原状；当输入为多维时，表示提取对应维度的列元素

import tensorflow as tf
a = tf.constant([[1, 2, 3, 4], [4, 3, 2, 1], [1, 3, 5, 6], [1, 2, 3, 5]])
#a为二维数组
sess = tf.InteractiveSession()
b = tf.transpose(a, [1, 0])
c  = tf.reshape(a, [-1, 4, 4])
sess.run(a)
sess.run(b)
sess.run(c)
'''
>>> sess.run(a)
array([[1, 2, 3, 4],
       [4, 3, 2, 1],
       [1, 3, 5, 6],
       [1, 2, 3, 5]])
>>> sess.run(b)
array([[1, 4, 1, 1],
       [2, 3, 3, 2],
       [3, 2, 5, 3],
       [4, 1, 6, 5]])
       #原矩阵转置
  >>> sess.run(c)
array([[[1],
        [4],
        [1],
        [1]],

       [[2],
        [3],
        [3],
        [2]],

       [[3],
        [2],
        [5],
        [3]],

       [[4],
        [1],
        [6],
        [5]]])    
        #先将原矩阵转换为三维数组，然后将各列元素提取
'''

4、tf.cast(input, tf.float32/…)

将input数据类型进行转换为目标类型

5、tf.argmax(input, axis = 0/1)

axis = 0, 输出input中列最大元素首次出现的index
axis = 1, 输出input中行最大元素首次出现的index

6、tf.truncated_normal(shape, mean, stddev)

a = tf.truncated_normal([2, 1], stddev = 0)
#表示2X1的二维矩阵，其中[]中的元素个数决定形成矩阵维度
b = tf.truncated_normal([5, 5, 1, 6], stddev = 0)
#表示形成四维，5X1矩阵，并且有5块，6列元素

7、tf.nn.conv2d(input, filter, strides, padding)

针对padding = 'SAME || VALID'进行解释
因为对图像的卷积操作对图像的输入维度及滤波器维度要求严格，并且为了使输出维度可以保持原维度或乘积维度，所以TensorFlow提供padding以供设计者灵活调用。
例如： a = tf.constant([1, 1, 1, 1, -1, -1, -1, 2, 3, 2, 1, 5], dtype = tf.float32) a = tf.reshape(a, [1, 4, 4, 1]) b = tf.constant([1, -1, 2, -3]) b = tf.reshape(b, [1, 4, 1, 1])
则a(3X4)、b(4X1)矩阵的具体形式如下：
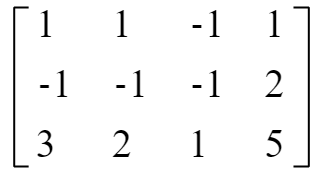
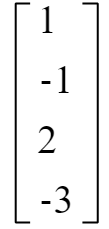
矩阵a为3X4矩阵在这里插入图片描述
当padding = 'VALID'时，因为VALID是对原矩阵直接进行卷积，所以最终得到3X1矩阵，其结果如下：

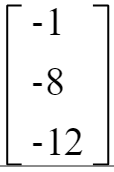
在这里插入图片描述
当padding = ‘SAME’时，因为SAME时保证输出矩阵维度和输入矩阵维度相等，所以运算过程中对原矩阵进行加0操作，此时a矩阵形式如下：

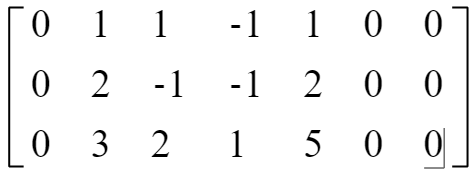
而此时b矩阵保持不变；此时a与b的卷积结果为：

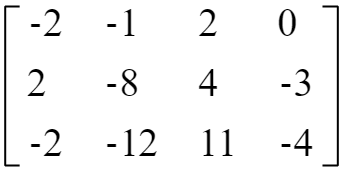
8、tf.nn.softmax(input)，注：此时input应该是一个Tensor

该函数的作用就是根据softmax公式对给定的Tensor进行归一化操作，例如：

import tensorflow as tf
sess = tf.Session()
sess.run(tf.nn.softmax(tf.constant([1, 2, 3], dtype = tf.float32)))
#计算后的结果为：
'''
array([0.09003057, 0.24472848, 0.66524094], dtype=float32)
'''

9、tf.reduce_sum(input, axis)

该函数是计算给定矩阵的求和，例如：

'''
>>> sess.run(tf.reduce_sum([[1, 2, 3], [4, 5, 6], [7, 8, 9]]))
45
>>> sess.run(tf.reduce_sum([[1, 2, 3], [4, 5, 6], [7, 8, 9]], axis = 0))#按列求和
array([12, 15, 18])
>>> sess.run(tf.reduce_sum([[1, 2, 3], [4, 5, 6], [7, 8, 9]], axis = 1))#按行求和
array([ 6, 15, 24])
'''

并且：tf.reduce_mean()类似于上述函数，只不过该函数是求均值