本文学习内容来自《TensorFlow深度学习应用实践》
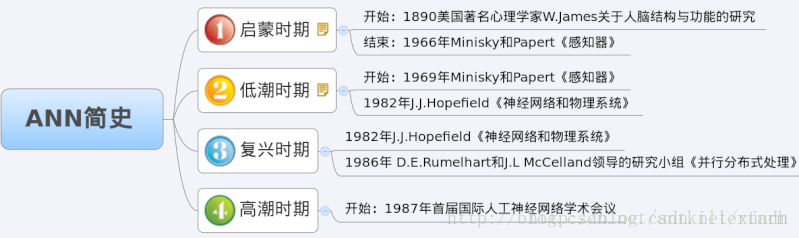
ANN简史
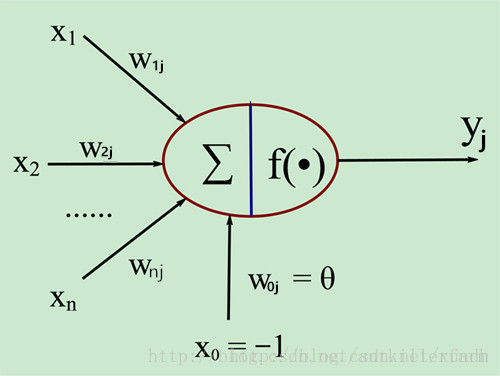
MP模型
MP神经元模型是1943年,由Warren McCulloch和Walter Pitts提出的。
即:
y
j
=
∑
i
=
1
n
w
i
j
x
i
−
θ
j
y_j=sum _{i=1}^nw_{ij}x_i-theta_j
yj=i=1∑nwijxi−θj
即逻辑回归模型。
生物神经元和MP神经元模型的对应关系如下表:
| 生物神经元 | MP神经元模型 |
|---|---|
| 神经元 | j |
| 输入信号 | x i x_i xi |
| 权值 | w i j w_{ij} wij |
| 输出信号 | y j y_j yj |
| 总和 | ∑ sum ∑ |
| 膜电位 | ∑ i = 1 n w i j x i sum _{i=1}^nw_{ij}x_i ∑i=1nwijxi |
| 阈值 | θ j theta_j θj |
BP神经网络简介
在人工神经网络的发展历史上,感知机(Multilayer Perceptron,MLP)网络曾对人工神经网络的发展发挥了极大的作用,也被认为是一种真正能够使用的人工神经网络模型,它的出现曾掀起了人们研究人工神经元网络的热潮。单层感知网络(M-P模型)做为最初的神经网络,具有模型清晰、结构简单、计算量小等优点。但是,随着研究工作的深入,人们发现它还存在不足,例如无法处理非线性问题,即使计算单元的作用函数不用阀函数而用其他较复杂的非线性函数,仍然只能解决解决线性可分问题.不能实现某些基本功能,从而限制了它的应用。增强网络的分类和识别能力、解决非线性问题的唯一途径是采用多层前馈网络,即在输入层和输出层之间加上隐含层。构成多层前馈感知器网络。
20世纪80年代中期,David Runelhart。Geoffrey Hinton和Ronald W-llians、DavidParker等人分别独立发现了误差反向传播算法(Error Back Propagation Training),简称BP,系统解决了多层神经网络隐含层连接权学习问题,并在数学上给出了完整推导。人们把采用这种算法进行误差校正的多层前馈网络称为BP网。
BP神经网络具有任意复杂的模式分类能力和优良的多维函数映射能力,解决了简单感知器不能解决的异或(Exclusive OR,XOR)和一些其他问题。从结构上讲,BP网络具有输入层、隐藏层和输出层;从本质上讲,BP算法就是以网络误差平方为目标函数、采用梯度下降法来计算目标函数的最小值。
BP算法的缺点
传统的BP算法,理论上可以支持任意深度的神经网络,但实际使用中,很少能支持3层以上的神经网络。
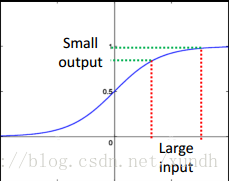
随着层数的增多,反向传递的残差梯度会越来越小,这样的现象,被称作梯度消失(Vanishing Gradient)。它导致的结果是,虽然靠近输出端的神经网络已经训练好了,但输入端的神经网络仍处于随机状态。也就是说,靠近输入端的神经网络,有和没有都是一样的效果,完全体现不了深度神经网络的优越性。
和梯度消失相反的概念是梯度爆炸(Vanishing Explode),也就是神经网络无法收敛。
参考:http://blog.csdn.net/antkillerfarm/article/details/74187428?locationNum=3&fps=1
BP神经网络的两个重要算法
最小二乘法(LS算法)
最小二乘法(又称最小平方法)是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据,并使得这些求得的数据与实际数据之间误差的平方和为最小。最小二乘法还可用于曲线拟合。其他一些优化问题也可通过最小化能量或最大化熵用最小二乘法来表达。
梯度下降算法
梯度下降是迭代法的一种,可以用于求解最小二乘问题(线性和非线性都可以)。在求解机器学习算法的模型参数,即无约束优化问题时,梯度下降(Gradient Descent)是最常采用的方法之一,另一种常用的方法是最小二乘法。在求解损失函数的最小值时,可以通过梯度下降法来一步步的迭代求解,得到最小化的损失函数和模型参数值。反过来,如果我们需要求解损失函数的最大值,这时就需要用梯度上升法来迭代了。在机器学习中,基于基本的梯度下降法发展了两种梯度下降方法,分别为随机梯度下降法和批量梯度下降法。
以上引自《百度百科》,后面章节再详细讲解最小二乘法与梯度下降算法。
BP算法讲解
数学上通过建立复杂的高次多元的函数解决复杂模型拟合的问题,但大多数都失败,因为过于复杂的函数式是无法进行求解,也就是其公式的获取不可能。
基于前人的研究,科研工作人员发现可以通过神经网络来表示这样的一个一一对应的关系,而神经网络本质就是一个多元复合函数,通过增加神经网络的层次和神经单元,可以更好地表达函数的复合关系。
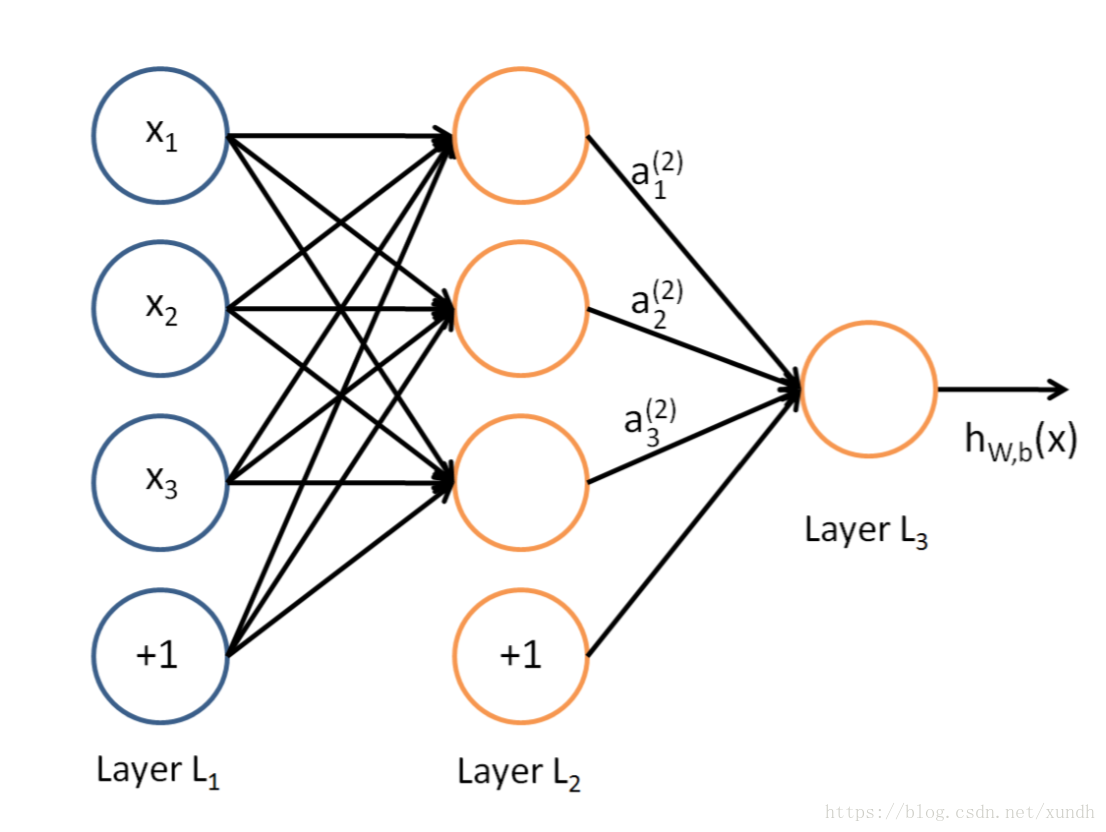
这是多层神经网络的一个图像表达方式。可以通过设置输入层、隐藏层与输出层可以形成一个多元函数求解相关问题。
定义一、 前向传播算法
隐藏层输出值定义:
a
h
H
l
=
W
h
H
l
∗
X
i
a_h^{Hl}=W_h^{Hl}*X_i
ahHl=WhHl∗Xi
b h H l = f ( a h H l ) b_h^{Hl}=f(a_h^{Hl}) bhHl=f(ahHl)
其中 X i X_i Xi 是当前节点的输入值, W h H l 是 连 接 到 此 节 点 的 权 重 , W^{Hl}_h是连接到此节点的权重, WhHl是连接到此节点的权重,a_h{Hl}是输出值。 f f f是当前阶段的激活函数, b h H l b_h{Hl} bhHl为当前节点的输入值经过计算后被激活的值。
输出层定义:
a
k
=
∑
W
h
k
∗
b
h
H
l
a_k=sum{W_{hk}*b_h^{Hl}}
ak=∑Whk∗bhHl
其中
W
h
k
W_{hk}
Whk为输入的权重,
b
h
H
l
b_h^{Hl}
bhHl为输入到输出节点的输入值。这里对所有输入值进行权重计算后求得的值,作为神经网络的最后输出值
a
k
a_k
ak。
定义二、反射传播算法
与前向传播类似,需要首先定义两个值
δ
k
delta_k
δk与
δ
h
H
l
delta_h^{Hl}
δhHl:
δ
k
=
∂
L
∂
a
k
=
(
Y
−
T
)
delta_k = frac {partial L} {partial a_k} = (Y-T)
δk=∂ak∂L=(Y−T)
δ h H l = ∂ L ∂ a h H l delta_h^{Hl} = frac {partial L} {partial a_h^{Hl}} δhHl=∂ahHl∂L
其中 δ k delta_k δk 为输出层的误差项,其计算值为真实值与模型计算值之间的差值。 Y Y Y 是计算值, T T T是输出真实值。 δ h H l delta_h^{Hl} δhHl为输出层的误差。
反馈神经网络的计算公式
δ
h
H
l
=
∂
L
∂
a
h
H
l
delta_h^{Hl} = frac {partial L} {partial a_h^{Hl}}
δhHl=∂ahHl∂L
= ∂ L ∂ b h H l ∗ ∂ b h H l ∂ a h H l = frac {partial L} {partial b_h^{Hl}} * frac {partial b_h^{Hl}} {partial a_h^{Hl}} =∂bhHl∂L∗∂ahHl∂bhHl
= ∂ L ∂ b h H l ∗ f ′ ( a h H l ) = frac {partial L} {partial b_h^{Hl}} * f'(a_h^{Hl}) =∂bhHl∂L∗f′(ahHl)
= ∂ L ∂ a k ∗ ∂ a k ∂ b h H l ∗ f ′ ( a h H l ) = frac {partial L} {partial a_k} * frac {partial a_k} {partial b_h^{Hl}} * f'(a_h^{Hl}) =∂ak∂L∗∂bhHl∂ak∗f′(ahHl)
= δ k ∗ ∑ W h k ∗ δ k ∗ f ′ ( a h H l ) = delta_k * sum{W_{hk} * delta_k * f'(a_h^{Hl})} =δk∗∑Whk∗δk∗f′(ahHl)
= ∑ W h k ∗ δ k ∗ f ′ ( a h H l ) = sum{W_{hk} * delta_k * f'(a_h^{Hl})} =∑Whk∗δk∗f′(ahHl)
即当前层输出值对误差的梯度可以通过下一层的误差与权重和输入值的梯度乘积获得。
或表示为:
δ
l
=
∑
W
i
j
l
∗
δ
j
l
+
1
∗
f
′
(
a
i
l
)
delta^l = sum{W_{ij}^l * delta_j^{l+1} * f'(a_i^l)}
δl=∑Wijl∗δjl+1∗f′(ail)
可以看到,通过更为泛化的公式,把当前层的输出对输入的梯度计算转化成求下一层级的梯度计算值。
定义三、权重的更新
θ = θ − α ( f ( θ ) − y i ) x i theta = theta-alpha(f(theta)-y_i)x_i θ=θ−α(f(θ)−yi)xi
即:
W
j
i
=
W
j
i
+
α
∗
δ
j
l
∗
x
j
i
W_{ji} = W_{ji} + alpha * delta_j^l * x_{ji}
Wji=Wji+α∗δjl∗xji
b j i = b j i + α ∗ δ j l b_{ji} = b{ji} + alpha * delta_j^l bji=bji+α∗δjl
其中ji表示为反射传播时对应的节点系数,通过对 δ j l delta_j^l δjl的计算,就可以更新对应的权重值。
反馈神经网络的激活函数
以前主要使用Sigmod函数,近年来涌现出大量新的激活函数模型,如Maxout、Tanh、 ReLU模型。
一个示例:
https://www.cnblogs.com/charlotte77/p/5629865.html
最后
以上就是感性小海豚最近收集整理的关于Tensorflow 入门学习3 重要算法基础ANN简史MP模型BP神经网络简介BP算法的缺点BP神经网络的两个重要算法的全部内容,更多相关Tensorflow内容请搜索靠谱客的其他文章。








发表评论 取消回复