电路分析基础知识点总结(持续更新)
文章目录
- 电路分析基础知识点总结(持续更新)
- 电阻电路分析
- 动态电路分析(增加电感,电容元件)
- 期中考试总结
- 正弦稳态电路分析
- 互感与理想变压器
- 网络函数和频率响应
电阻电路分析
1、电路模型
组成:电源+负载+导线
功能:其一,进行能量的传输、分配与转换;其二,实现信息的传递与处理。
集总参数电路:(实际电路的尺寸)l<<(电路工作时的电磁波的波长)
λ
lambda
λ【
l
<
0.1
λ
l<0.1lambda
l<0.1λ】
2、电路变量(相互关联参考方向)
电流:
i
(
t
)
=
d
q
(
t
)
d
t
i_{(t)}=frac{dq_{(t)}}{dt}
i(t)=dtdq(t)
电压:
u
(
t
)
=
d
w
(
t
)
d
q
(
t
)
u_{(t)}=frac{dw_{(t)}}{dq_{(t)}}
u(t)=dq(t)dw(t)
电功率:
p
(
t
)
=
d
w
(
t
)
d
t
p_{(t)}=frac{dw_{(t)}}{dt}
p(t)=dtdw(t)【区分吸收功率与产生功率】

3、电路分析基础定律
欧姆定律(OL):
u
(
t
)
=
R
i
(
t
)
u_{(t)} = Ri_{(t)}
u(t)=Ri(t) or
i
(
t
)
=
G
u
(
t
)
i_{(t)} = Gu_{(t)}
i(t)=Gu(t)
基尔霍夫电流定律(KCL):对于集总参数电路的任意节点,在任一时刻流出该节点的电流之和等于流入该节点的电流之和。
Σ
k
=
1
m
i
k
(
t
)
=
0
Sigma_{k=1}^mi_{k(t)} = 0
Σk=1mik(t)=0
基尔霍夫电压定律(KVL):对任意集总参数电路,在任一时刻,沿任意闭合路径巡行一周,各段电路电压的代数和恒为零。
Σ
k
=
1
m
u
k
(
t
)
=
0
Sigma_{k=1}^mu_{k(t)} = 0
Σk=1muk(t)=0
4、理想电源
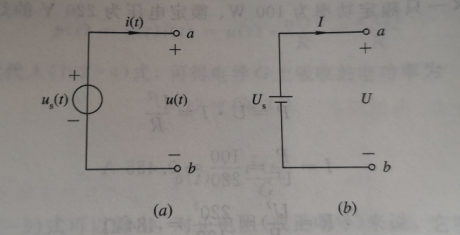
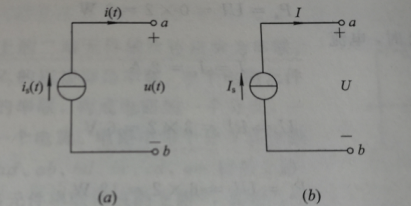
5、电路等效
若B和C具有相同的电压电流关系(VCR)即相同的伏安特性关系(VAR),则称B与C互为等效的。
1)电阻串并联等效
串联:
R
=
R
1
+
R
2
+
⋯
R = R_1+R_2+cdots
R=R1+R2+⋯
并联:
1
R
=
1
R
1
+
1
R
2
+
⋯
frac{1}{R}=frac{1}{R_1}+frac{1}{R_2}+cdots
R1=R11+R21+⋯
【电导与电阻恰好相反!】
2)电源等效
电压源串联:
u
s
=
u
s
1
+
u
s
2
+
⋯
u_s = u_{s1}+u_{s2}+cdots
us=us1+us2+⋯
电流源并联:
i
s
=
i
s
1
+
i
s
2
+
⋯
i_s = i_{s1}+i_{s2}+cdots
is=is1+is2+⋯
任意元件与电压源并联为电压源
任意元件与电流源串联为电流源
电压源串联电阻与电流源并联电阻可相互等效
电源的等效转移:

*
Δ
−
Y
变
换
Delta-Y变换
Δ−Y变换
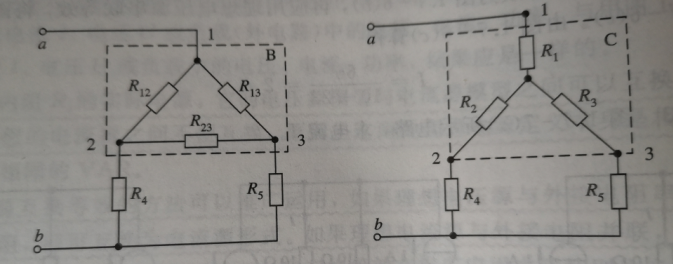
Δ
Delta
Δ变为
Y
Y
Y:
R
1
=
R
12
R
13
R
12
+
R
23
+
R
13
R_1=frac{R_{12}R_{13}}{R_{12}+R_{23}+R_{13}}
R1=R12+R23+R13R12R13
R
2
=
R
12
R
23
R
12
+
R
23
+
R
13
R_2=frac{R_{12}R_{23}}{R_{12}+R_{23}+R_{13}}
R2=R12+R23+R13R12R23
R
3
=
R
13
R
23
R
12
+
R
23
+
R
13
R_3=frac{R_{13}R_{23}}{R_{12}+R_{23}+R_{13}}
R3=R12+R23+R13R13R23
Y
Y
Y变为
Δ
Delta
Δ:
R
12
=
R
1
R
2
+
R
2
R
3
+
R
1
R
3
R
3
R_{12}=frac{R_1R_2+R_2R_3+R_1R_3}{R_3}
R12=R3R1R2+R2R3+R1R3
R
23
=
R
1
R
2
+
R
2
R
3
+
R
1
R
3
R
1
R_{23}=frac{R_1R_2+R_2R_3+R_1R_3}{R_1}
R23=R1R1R2+R2R3+R1R3
R
13
=
R
1
R
2
+
R
2
R
3
+
R
1
R
3
R
2
R_{13}=frac{R_1R_2+R_2R_3+R_1R_3}{R_2}
R13=R2R1R2+R2R3+R1R3
6、受控源
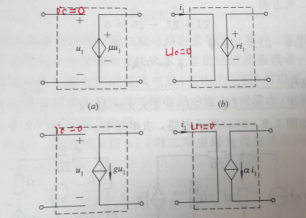
7、进阶的电路分析法
1)回路电流法
R
11
i
A
+
R
12
i
B
+
R
13
i
C
=
u
s
11
R_{11}i_A+R_{12}i_B+R_{13}i_C=u_{s11}
R11iA+R12iB+R13iC=us11
R
21
i
A
+
R
22
i
B
+
R
23
i
C
=
u
s
21
R_{21}i_A+R_{22}i_B+R_{23}i_C=u_{s21}
R21iA+R22iB+R23iC=us21
R
31
i
A
+
R
32
i
B
+
R
33
i
C
=
u
s
31
R_{31}i_A+R_{32}i_B+R_{33}i_C=u_{s31}
R31iA+R32iB+R33iC=us31

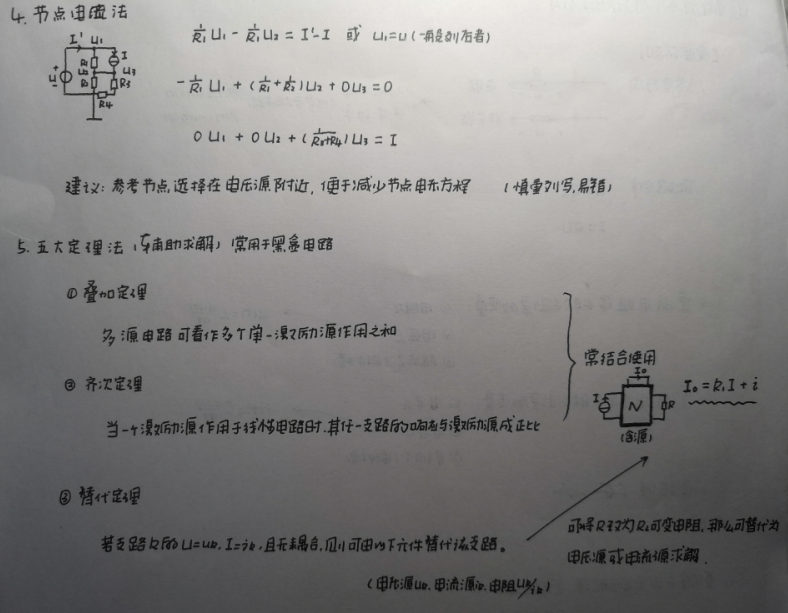
2)节点电压法
G
11
i
A
+
G
12
i
B
+
G
13
i
C
=
i
s
11
G_{11}i_A+G_{12}i_B+G_{13}i_C=i_{s11}
G11iA+G12iB+G13iC=is11
G
21
i
A
+
G
22
i
B
+
G
23
i
C
=
i
s
21
G_{21}i_A+G_{22}i_B+G_{23}i_C=i_{s21}
G21iA+G22iB+G23iC=is21
G
31
i
A
+
G
32
i
B
+
G
33
i
C
=
i
s
31
G_{31}i_A+G_{32}i_B+G_{33}i_C=i_{s31}
G31iA+G32iB+G33iC=is31

3)叠加定理:在任何由线形元件,线形受控源及独立源组成的线形电路中,每一支路的响应(电压或电流)都可以看成是各个独立源单独作用时,在该支路中产生的响应的代数和。
4)齐次定理
当一个激励源(独立电压源或独立电流源)作用于线性电路时,其任意支路的响应(电压或电流)与该激励源成正比。
5)替代定理
具有唯一解的电路中,若知道某支路k的电压为
u
k
u_k
uk,电流为
i
k
i_k
ik,且该支路与电路中其他支路无耦合,则无论该支路是由什么元件组成的,都可以用下列一个元件去代替:电压源、电流源、电阻。
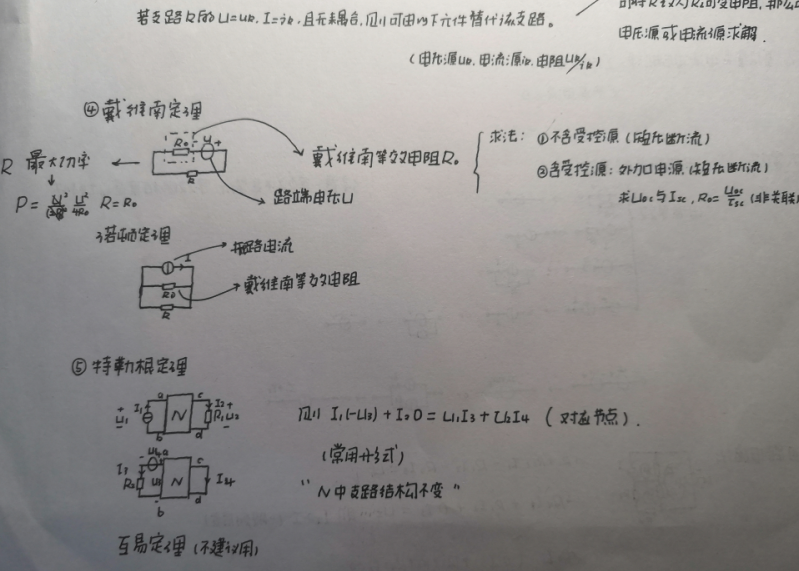
6)戴维宁定理
一个含有独立源、线性受控源、线性电阻的二端网络N,对其两个端子来说都可以等效为一个电压源串联内阻的模型。其理想电压源的数值为有源二端电路N的两个端子间的开路电压
u
o
c
u_{oc}
uoc,串联的内阻为N内部所有独立源等于零(理想电压源短路,理想电流源开路),受控源保留时的等效电阻
R
e
q
R_{eq}
Req,常记为
R
0
R_0
R0。
求
R
0
R_0
R0的两种方法:
外加电源法:电流与电压相对于外电路取相互关联方向
开路短路法:电流电压取相互关联方向
【需灵活应用戴维南定理】
7)诺顿定理
一个含有独立源、线性受控源、线性电阻的二端网络N,对其两个端子来说都可以等效为一个电流源并联内阻的模型。其理想电流源的数值为有源二端电路N的两个端子间的短路电流
u
o
c
u_{oc}
uoc,并联的内阻为N内部所有独立源等于零(理想电压源短路,理想电流源开路),受控源保留时的等效电阻
R
e
q
R_{eq}
Req,常记为
R
0
R_0
R0。
8)特勒根定理

9)互易定理
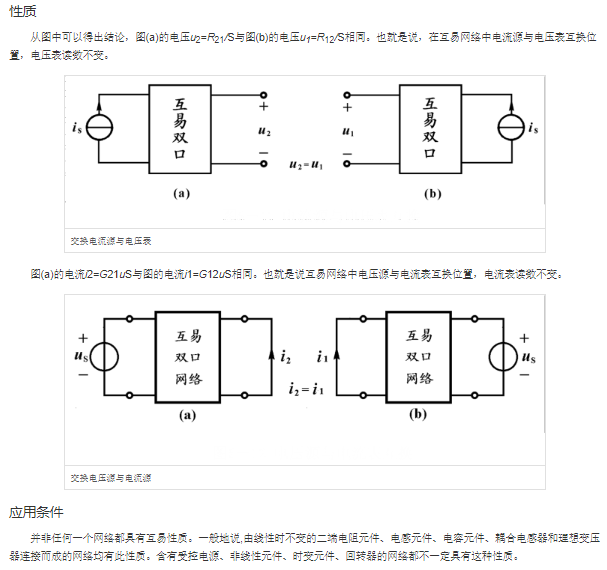
8、最大功率传输定理
戴维南等效+
P
m
a
x
=
U
2
4
R
e
q
P_{max} = frac{U^2}{4R_{eq}}
Pmax=4ReqU2
动态电路分析(增加电感,电容元件)
1、电感元件
磁链与电流满足:
ψ
(
t
)
=
L
i
(
t
)
psi(t) = Li(t)
ψ(t)=Li(t)
VCR微分形式
u
(
t
)
=
L
d
i
(
t
)
d
t
u(t) = Lfrac{di(t)}{dt}
u(t)=Ldtdi(t)
VCR积分形式
i
(
t
)
=
1
L
∫
−
∞
t
u
(
α
)
d
α
i(t) = frac{1}{L}int_{-infty}^t u(alpha)dalpha
i(t)=L1∫−∞tu(α)dα
电感元件储能:
w
L
(
t
)
=
1
2
L
i
2
(
t
)
w_L(t) = frac{1}{2}Li^2(t)
wL(t)=21Li2(t)
2、电容元件
电荷与电压满足:
q
(
t
)
=
C
u
(
t
)
q(t) = Cu(t)
q(t)=Cu(t)
VCR微分形式
i
(
t
)
=
C
d
u
(
t
)
d
t
i(t) = Cfrac{du(t)}{dt}
i(t)=Cdtdu(t)
VCR积分形式
u
(
t
)
=
1
C
∫
−
∞
t
i
(
α
)
d
α
u(t) = frac{1}{C}int_{-infty}^t i(alpha)dalpha
u(t)=C1∫−∞ti(α)dα
电感元件储能:
w
L
(
t
)
=
1
2
C
u
2
(
t
)
w_L(t) = frac{1}{2}Cu^2(t)
wL(t)=21Cu2(t)
3、电容元件的串并联等效遵循电导串并联规律,电感元件串并联等效遵循电阻串并联规律
4、动态电路方程(含电感和电容的电路)
对于动态电路分析,主要解决一阶电路方程即可。
规定参数
τ
tau
τ:
L
R
frac{L}{R}
RL or
R
C
RC
RC,单位:s
动态电路的求解方法:
1)微分方程法
*计算换路前后的稳态值:等效电容为开路,电感为短路。
*按照KVL/KCL列写微分方程
*解微分方程,并带入稳态值得到结果
2)三要素法(只能解一阶动态电路)
所谓三要素即:
①时常数
τ
tau
τ
②换路后一瞬间初始值
u
(
0
+
)
o
r
i
(
0
+
)
u(0+) or i(0+)
u(0+)ori(0+)
③无限长时间后的稳态值
u
(
∞
)
o
r
i
(
∞
)
u(infty) or i(infty)
u(∞)ori(∞)
将上述结果带入下式:
i
(
t
)
=
(
i
(
0
+
)
−
i
(
∞
)
)
e
−
t
τ
+
i
(
∞
)
i(t) = (i(0+) - i(infty))e^{-frac{t}{tau}}+i(infty)
i(t)=(i(0+)−i(∞))e−τt+i(∞)
u
(
t
)
=
(
u
(
0
+
)
−
u
(
∞
)
)
e
−
t
τ
+
u
(
∞
)
u(t) = (u(0+) - u(infty))e^{-frac{t}{tau}}+u(infty)
u(t)=(u(0+)−u(∞))e−τt+u(∞)
即可。
说明:对于求独立稳态值(电容电压,电感电流)可以等效直接求解。如果要求非独立稳态值,需要将电容等效为电压为稳态电压的电压源,电感等效为电流为稳态电流的电流源,在按照电阻电路求解。
三要素法的应用中,难点在黑盒电路的求解,其中要求灵活应用戴维南、特勒根、互易等黑盒电路处理方法。
5、强迫跃变情况(了解)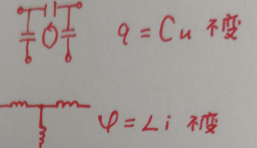
6、零状态响应和零输入响应
零状态响应:即动态元件初始值为0的响应(一般为换路前电路无源)
零输入响应:即换路后电路无源
全响应 = 零状态响应 + 零输入响应
7、阶跃函数与阶跃响应
阶跃函数:
ε
(
t
)
=
0
(
t
≤
0
−
)
;
1
(
t
≥
0
+
)
varepsilon(t) = 0 (tleq0_-);1(tgeq0_+)
ε(t)=0(t≤0−);1(t≥0+)
其作用相当于开关,在动态电路中将产生换路效果,并可以在时间上截取电路。
阶跃响应:应用阶跃函数求解动态电路(其换路作用),要记住,结果同样受阶跃函数制约,即不要忘记乘单位阶跃函数(
ε
(
t
)
varepsilon(t)
ε(t))
8、电路的时不变性质
电路的零状态响应形状与激励接入时间无关,或者说电路的激励延迟多长时间,其电路的l零状态响应也延迟多长时间,这样的电路称为时不变电路。
9、正弦激励下一阶电路响应
一个结论:若电路微分方程所用特征根的实部都小于零,这样的电路叫做渐进稳定电路。
运用以上知识求解将涉及复杂的三角变换,缺少实际应用价值,所以相量法就十分重要。
期中考试总结



正弦稳态电路分析
1、基础知识
正弦电路的三要素:振幅、角频率、初相
有效值:令正弦电流
i
i
i和直流电流
I
I
I分别通过两个阻值相等的电阻R,如果在相同的时间
T
T
T内,两个电阻消耗的能量相等,那么定义该直流电流的值为正弦电流
i
i
i的有效值
在正弦电路中有效值为
I
=
I
m
2
I = frac{I_m}{sqrt{2}}
I=2Im
在正弦稳态电路中的符号表示意义
| i ( t ) i(t) i(t) | 瞬时值 |
|---|---|
| I I I | 有效值 |
| I ^ hat I I^ | 相量形式 |
| I m I_m Im | 振幅值 |
| j j j | 虚数单元 |
| Z Z Z | 阻抗 |
| X L X_L XL | 感抗(X>0) |
| X C X_C XC | 容抗(X<0) |
| Y Y Y | 导纳 |
| B L B_L BL | 感纳(B<0) |
| B C B_C BC | 容纳(B>0) |
| P P P | 有功功率 |
| Q Q Q | 无功功率 |
| S S S | 视在功率( S = P 2 + Q 2 S = sqrt{P^2+Q^2} S=P2+Q2-) |
| S ~ tilde S S~ | 复功率 |
| w w w | 角频率 |
| ϕ phi ϕ | 初相 |
2、电流/电压的复数表示
若
i
(
t
)
=
I
m
c
o
s
(
w
t
+
ϕ
i
)
i(t) = I_mcos(wt+phi_i)
i(t)=Imcos(wt+ϕi),则
I
^
=
I
e
j
ϕ
i
=
I
∠
ϕ
i
hat I = Ie^{jphi_i} = I∠phi_i
I^=Iejϕi=I∠ϕi
若
u
(
t
)
=
U
m
c
o
s
(
w
t
+
ϕ
i
)
u(t) = U_mcos(wt+phi_i)
u(t)=Umcos(wt+ϕi),则
U
^
=
U
e
j
ϕ
i
=
U
∠
ϕ
i
hat U = Ue^{jphi_i} = U∠phi_i
U^=Uejϕi=U∠ϕi
3、VCR
对于此类电路,无论电阻,电感,电容均采用阻抗(导纳)思考,基本遵循电阻(电导)的VCR。
4、阻抗和导纳
阻抗:
Z
=
R
+
j
X
Z=R+jX
Z=R+jX
其中,R为电阻部分;X为电抗部分(X>0为感抗)。
电感:
X
L
=
w
L
X_L = wL
XL=wL
电容:
X
C
=
−
1
w
C
X_C = -frac{1}{wC}
XC=−wC1
导纳:
Y
=
G
+
j
B
Y = G + jB
Y=G+jB
其中,G为电导部分;B为电纳部分(B<0为感纳)。
电感:
B
L
=
−
1
w
L
B_L = -frac{1}{wL}
BL=−wL1
电容:
B
C
=
w
C
B_C = wC
BC=wC
导纳和阻抗的串并联遵循电阻和电导的串并联规律
5、相量法
正弦稳态电路中的运算应遵循复数运算法则,其中做相量图是直观易用的方法。
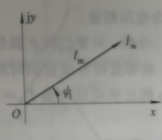
5、正弦稳态电路的相量分析法
对电阻电路适用的所有分析方法在正弦稳态电路中依然适用,但要遵循复数运算法则。
特别的:网孔电流法中互电阻被互阻抗替代,自电阻被自阻抗替代。节点电压法中互电导被互导纳替代,自电导被自导纳替代。
6、正弦稳态电路的功率
功率的计算仍与电阻功率计算方法一致,但要遵循复数运算规律。
有功功率:
P
=
U
I
c
o
s
ϕ
z
P = UIcosphi_z
P=UIcosϕz(单位:
W
W
W)
c
o
s
ϕ
z
cosphi_z
cosϕz称为功率因数,其中
ϕ
Z
phi_Z
ϕZ也叫阻抗角。
无功功率:
Q
=
U
I
s
i
n
ϕ
z
Q = UIsinphi_z
Q=UIsinϕz(单位:
v
a
r
var
var)
视在功率:
S
=
U
I
=
P
2
+
Q
2
S = UI = sqrt{P^2+Q^2}
S=UI=P2+Q2(单位:
V
⋅
A
Vcdot A
V⋅A)
复功率:
S
~
=
P
+
j
Q
tilde S = P + jQ
S~=P+jQ
一般的:有功功率由电阻产生,无功功率由电容电感产生。
7、最大功率问题
将戴维南等效电阻和路端电压的求法应用在复数运算规律下,可对应将电路简化为如下电路: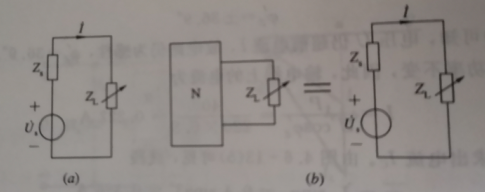
共轭匹配条件(当负载电阻和电抗可随意改变时用)
Z
L
=
Z
‾
s
Z_L = overline Z_s
ZL=Zs
即:
X
L
=
−
X
s
X_L = -X_s
XL=−Xs
R L = R s R_L = R_s RL=Rs
[这里的 X L X_L XL指的是负载阻抗而非感抗]
P L m a x = U s 2 4 R s P_{Lmax} = frac{U_s^2}{4R_s} PLmax=4RsUs2
模值匹配条件(当负载只能为纯电阻时用)
∣
Z
L
∣
=
∣
Z
s
∣
=
R
s
2
+
X
s
2
|Z_L| = |Z_s| = sqrt{R_s^2+X_s^2}
∣ZL∣=∣Zs∣=Rs2+Xs2
P L m a x = ∣ Z s ∣ U s 2 ( R s + ∣ Z s ∣ ) 2 + X s 2 P_{Lmax} = frac{|Z_s|U_s^2}{(R_s + |Z_s|)^2+X_s^2} PLmax=(Rs+∣Zs∣)2+Xs2∣Zs∣Us2
8、多频电路的响应
对于电流,电压的计算运用叠加定理即可
对于功率
P
0
=
P
1
+
P
2
P_0 = P_1 + P_2
P0=P1+P2 注意在同频下这种计算方法是错误的。
互感与理想变压器
1、耦合电感模型
k = 1时称为全耦合, k = 0时两者没有耦合。(当两电感线圈轴线垂直时即是这种情况)
M
=
k
L
1
L
2
M = ksqrt{L_1L_2}
M=kL1L2
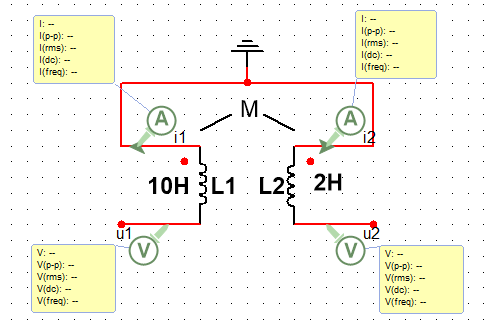
如图所示,为互感电感模型。该图中L1和L2为自电感,M为互电感,u1,u2均为下正上负,i1,i2方向已标出,都从同名端流出(流入)(都取关联参考方向)。
则有电压电流关系:
u
1
=
L
1
d
i
1
d
t
+
M
d
i
2
d
t
u_1 = L_1frac{di_1}{dt} + Mfrac{di_2}{dt}
u1=L1dtdi1+Mdtdi2
u 2 = L 2 d i 2 d t + M d i 1 d t u_2 = L_2frac{di_2}{dt} + Mfrac{di_1}{dt} u2=L2dtdi2+Mdtdi1
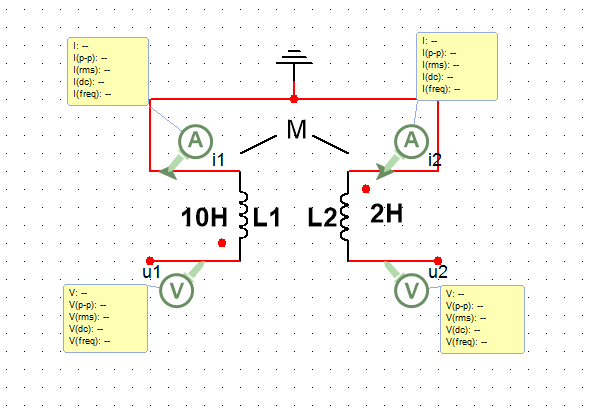
对于,电流i1,i2从异名端流入,此时电流电压仍取关联参考方向。
则有电压电流关系:
u
1
=
L
1
d
i
1
d
t
−
M
d
i
2
d
t
u_1 = L_1frac{di_1}{dt} - Mfrac{di_2}{dt}
u1=L1dtdi1−Mdtdi2
u 2 = L 2 d i 2 d t − M d i 1 d t u_2 = L_2frac{di_2}{dt} - Mfrac{di_1}{dt} u2=L2dtdi2−Mdtdi1
对于耦合电感电压电流关系的书写规则:
先写自感压降:若线圈上电压、电流取关联参考方向,则自感电压取正(
L
d
i
1
d
t
Lfrac{di_1}{dt}
Ldtdi1),反之取负(
−
L
d
i
1
d
t
-Lfrac{di_1}{dt}
−Ldtdi1)。
再写互感压降部分:若电流均从同名端流入或流出则该部分与自感压降同号,反之异号。
2、去耦等效
串联等效
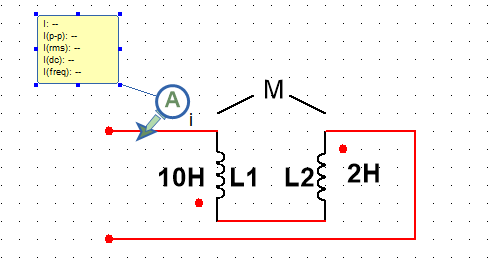
若电流均从同名端流入或流出(或者表述为:异名端相连),则等效电感为 L a b = L 1 + L 2 + 2 M L_{ab} = L_1+L_2+2M Lab=L1+L2+2M,上图记为这种情况,称为顺接串联。
若电流均从异名端流入或流出(或者表述为:同名端相连),则等效电感为 L a b = L 1 + L 2 − 2 M L_{ab} = L_1+L_2-2M Lab=L1+L2−2M,称为反接串联。
T型去耦等效
同名端为共端的T形去耦等效
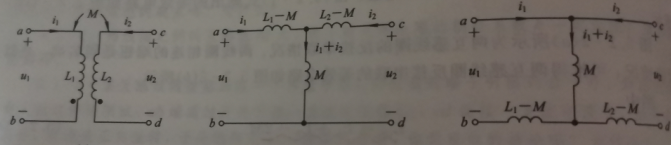
异名端为共端的T形去耦等效
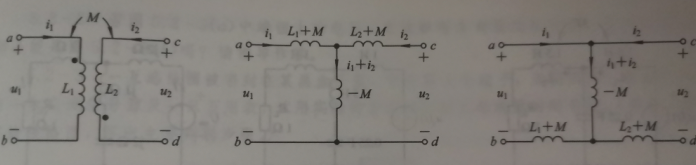
3、含互感电路的电路分析
总体思路仍然为以相量法处理电流电压关系,在这之前只需要进行去耦等效就可以了。
4、理想变压器
不同于互感电感,在理想变压器模型中已知量不在是自感和互感系数,而是匝数比。分析方法也随之改变,具体方法分两点阐述。
方法一:电流电压转换
对于下图模型(注意看电压取向和同名端的关系),电压关系为
u
1
u
2
=
N
1
N
2
=
n
frac{u_1}{u_2} = frac{N_1}{N_2} = n
u2u1=N2N1=n[注意:在进行变压关系计算时,电压比值取正还是取负,取决于电压参考方向和同名端的位置,而与两线圈中的电流参考方向无关]
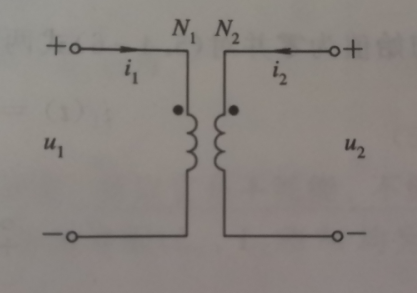
对于下图模型(注意看电流i取向和同名端的关系),电流关系为
u
1
u
2
=
−
N
2
N
1
=
−
1
n
frac{u_1}{u_2} = -frac{N_2}{N_1} = -frac{1}{n}
u2u1=−N1N2=−n1[注意:在进行变流关系计算时,电流比值取正还是取负,取决于电流参考方向和同名端的位置,而与两线圈中的电压参考方向无关]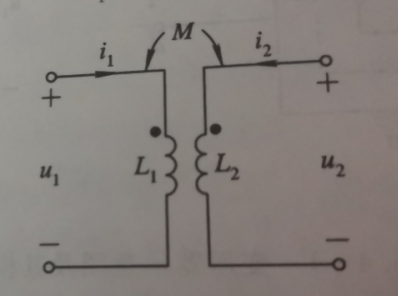
方法二:阻抗变换法
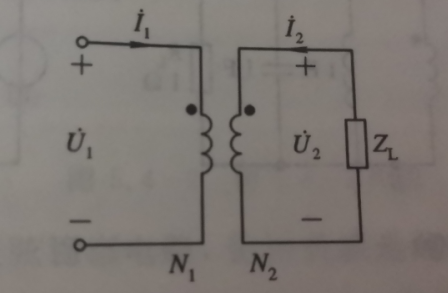
Z
i
n
=
n
2
Z
L
(
n
=
N
1
N
2
)
Z_{in} = n^2Z_L(n = frac{N_1}{N_2})
Zin=n2ZL(n=N2N1)
按照这个关系式,则理想变压器次级短路则相当于初级短路,次级开路即相当于初级开路
4、实际变压器(了解)
实际变压器简单可以分为全耦合空芯变压器,非全耦合空芯变压器,铁芯变压器
对于全耦合空芯变压器,其变压关系和理想变压器的变压关系是完全一样的。电流关系为
i
1
(
t
)
=
−
N
2
N
1
i
2
(
t
)
+
1
L
1
∫
0
t
u
1
(
θ
)
d
θ
i_1(t) = -frac{N_2}{N_1}i_2(t)+frac{1}{L_1}int_0^tu_1(theta)dtheta
i1(t)=−N1N2i2(t)+L11∫0tu1(θ)dθ.
其余模型均复杂的多,了解即可
网络函数和频率响应
1、网络函数
网络函数定义为电路的响应向量与电路的激励相量之比,以符号
H
(
j
w
)
H(jw)
H(jw)表示,即
H
(
j
w
)
=
响
应
激
励
/
激
励
相
量
H(jw) = 响应激励/激励相量
H(jw)=响应激励/激励相量
一般情况下,含动态元件电路的网络函数
H
(
j
w
)
H(jw)
H(jw)是频率的复函数,将它写为指数表示,有
H
(
j
w
)
=
∣
H
(
j
w
)
∣
e
j
ϕ
(
w
)
H(jw)=|H(jw)|e^{jphi(w)}
H(jw)=∣H(jw)∣ejϕ(w)
网络的幅频特性:
H
(
j
w
)
H(jw)
H(jw)与w的关系曲线称为网络的频率特性
网络的相频特性:
ϕ
(
w
)
phi(w)
ϕ(w)与w的关系曲线称为网络的相频特性
这里明确一下截止频率
w
c
w_c
wc和通频带
B
W
BW
BW的概念
2、RC(L)一阶电路的频率特性(熟悉推导过程,尽量记住网络函数形式)
低通网络
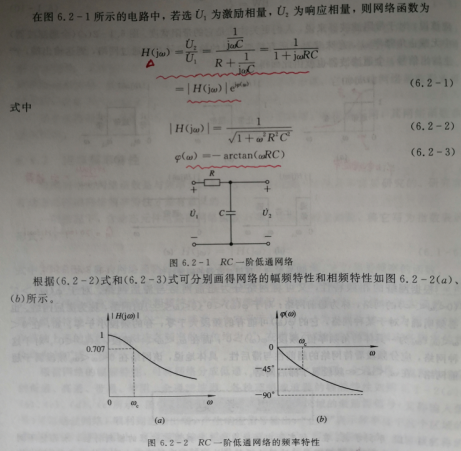
引入截至角频率后,我们可以轻易得到
H
(
j
w
)
=
∣
H
(
j
0
)
∣
1
1
+
j
w
w
c
H(jw) = |H(j0)|frac{1}{1+jfrac{w}{w_c}}
H(jw)=∣H(j0)∣1+jwcw1
高通网络
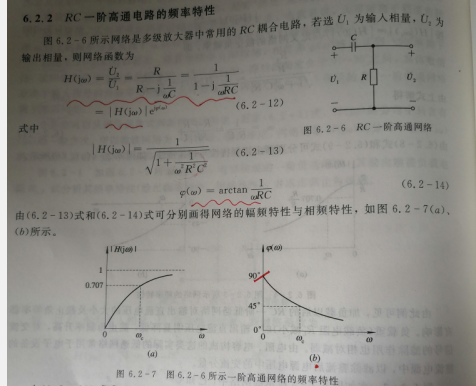
引入截至角频率后,我们可以轻易得到
H
(
j
w
)
=
∣
H
(
j
∞
)
∣
1
1
−
j
w
c
w
H(jw) = |H(jinfty)|frac{1}{1-jfrac{w_c}{w}}
H(jw)=∣H(j∞)∣1−jwwc1
如果以分贝为单位表示网络的幅频特性:
H
(
j
w
)
=
20
l
g
∣
H
(
j
w
)
∣
d
B
H(jw) = 20lg|H(jw)|dB
H(jw)=20lg∣H(jw)∣dB
所以截至频率又称为3分贝角频率
一点自己的感悟:我们可以看出来,上面所讲的高通网络和低通网络实际上是一个电路,其区别在于高通网络以电容电压为响应,低通网络以电阻电压为响应。所以说,这里所讲的低通和高通是对响应而言的,与电路没有绝对的关系。那么显然将电容换为电感也可以产生相似的网络特性。这对我们下面对RCL串并联谐振电路的理解有很大帮助
3、RC二阶电路的频率特性
适当了解,不做要求
4、常见的RCL串联谐振电路的频率特性
电路模型:串联
谐振频率:
w
0
=
1
L
C
r
a
d
/
s
w_0 = frac{1}{sqrt{LC}}rad/s
w0=LC1rad/s
特性阻抗:
ρ
=
w
0
L
=
1
w
0
C
=
L
C
Ω
rho = w_0L = frac{1}{w_0C}=sqrt{frac{L}{C}}Omega
ρ=w0L=w0C1=CLΩ
品质因数:
Q
=
w
0
L
r
=
1
r
w
0
C
Q = frac{w_0L}{r} = frac{1}{rw_0C}
Q=rw0L=rw0C1
谐振特点:
Z
0
=
r
Z_0 = r
Z0=r
通频带:
B
W
=
w
0
Q
BW = frac{w_0}{Q}
BW=Qw0
5、实用RCL并联谐振电路的频率特性
电路模型:不完全并联(具体看下图)
谐振频率:
w
0
=
1
L
C
r
a
d
/
s
w_0 = frac{1}{sqrt{LC}}rad/s
w0=LC1rad/s(近似,满足高Q特点)
特性阻抗:
ρ
=
w
0
L
=
1
w
0
C
=
L
C
Ω
rho = w_0L = frac{1}{w_0C}=sqrt{frac{L}{C}}Omega
ρ=w0L=w0C1=CLΩ
品质因数:
Q
=
w
0
L
r
=
1
r
w
0
C
Q = frac{w_0L}{r} = frac{1}{rw_0C}
Q=rw0L=rw0C1
谐振特点:
Z
0
=
L
r
C
=
Q
2
r
=
R
0
Z_0 = frac{L}{rC} = Q^2r = R_0
Z0=rCL=Q2r=R0
通频带:
B
W
=
w
0
Q
r
a
d
/
s
BW = frac{w_0}{Q}rad/s
BW=Qw0rad/s
6、严格并联的RCL谐振电路的频率特性(了解)
电路模型:严格并联
谐振频率:
w
0
=
1
L
C
r
a
d
/
s
w_0 = frac{1}{sqrt{LC}}rad/s
w0=LC1rad/s
特性阻抗:
ρ
=
w
0
L
=
1
w
0
C
=
L
C
Ω
rho = w_0L = frac{1}{w_0C}=sqrt{frac{L}{C}}Omega
ρ=w0L=w0C1=CLΩ
品质因数:
Q
=
R
w
0
L
=
w
0
R
C
Q = frac{R}{w_0L} = w_0RC
Q=w0LR=w0RC
谐振特点:
Z
=
r
Z = r
Z=r
通频带:
B
W
=
w
0
Q
r
a
d
/
s
BW = frac{w_0}{Q}rad/s
BW=Qw0rad/s

最后
以上就是仁爱御姐最近收集整理的关于电路分析基础知识点总结电路分析基础知识点总结(持续更新)的全部内容,更多相关电路分析基础知识点总结电路分析基础知识点总结(持续更新)内容请搜索靠谱客的其他文章。








发表评论 取消回复