BPSK 二相相移键控
先来了解一下BPSK(Binary Phase Shift Keying,二相相移键控)
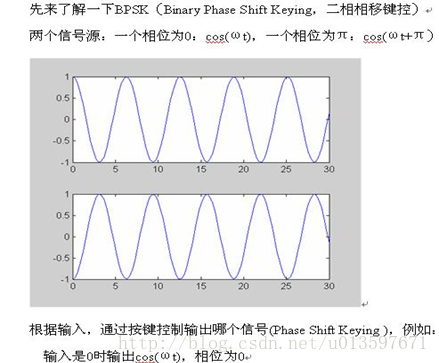
二.PSK(相移键控)和IQ调制的关系:
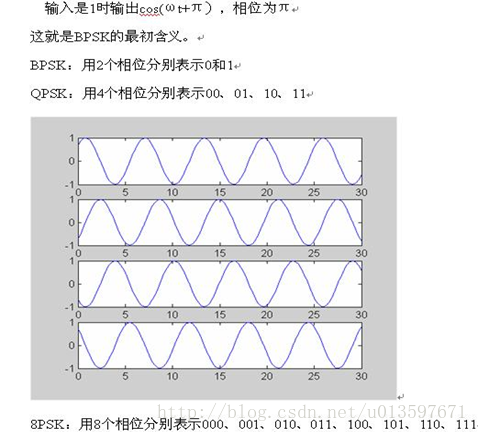
PSK:相移键控方法是通过改变载波信号的相位值来表示数字信号 1,0的。当然,在实际信号的传输过程中,经常会把二进制信号按照M个比特作为一组传输,这就是MPSK。(PSK调制幅度不变,改变相位)
比如说:如果我们把2个比特作为一组,那么每一组二进制信号就会有00,01,10,11四种组合方式,那么我们就需要s(t)用4种不同的相位值分别来表示00,01,10和11,这样的调制方式我们成为QPSK调制。
2.1 用IQ调制实现QPSK调制
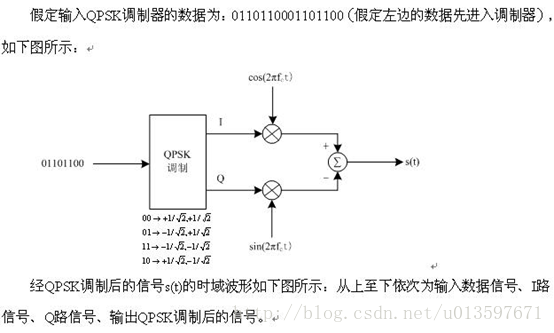
首先,我们假设输入的I 路和Q 路信号分别为:+1+1、+1-1、-1+1、-1-1。那么根据上面IQ调制的流程图,我们分别看看输出的s(t)信号是怎么样的:
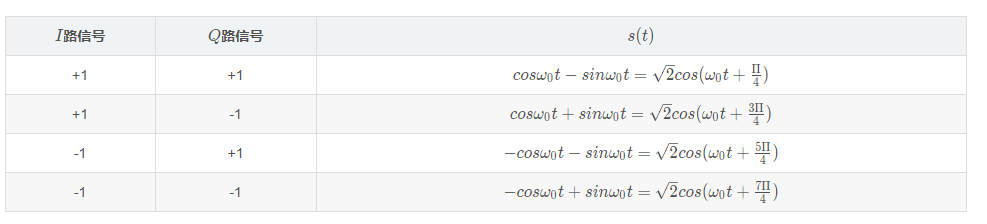
如果我们要把s(t)的幅度变成1,那么只需要将上面I,Q信号对应第改为-1sqrt{2},+1sqrt{2}即可
而我们发现:
![]()
![]()
因为要使s(t)的幅度A为1,就可以直接根据上式得:令I=cos(θ),Q=sin(θ),其中符合要求的θ值。
在这里直接令依次θ=pi/4,3*(pi/4),5*(pi/4),7*(pi/4),,
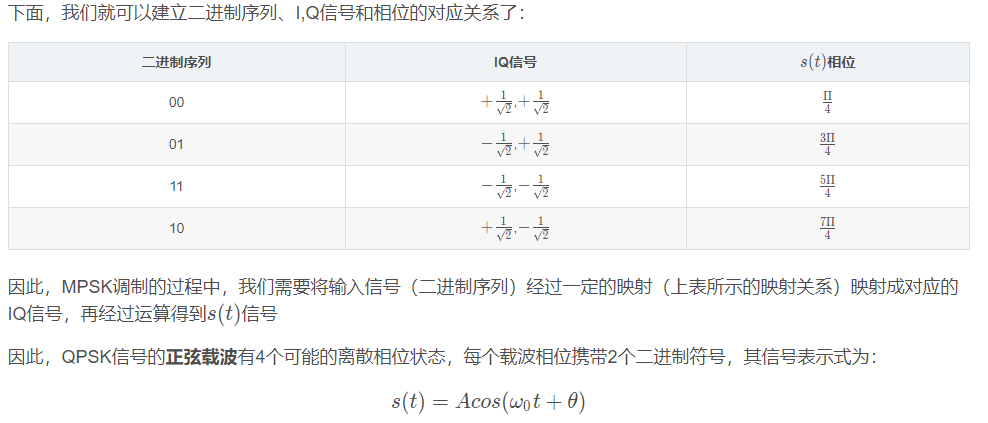
下图是QPSK调制的星座图:
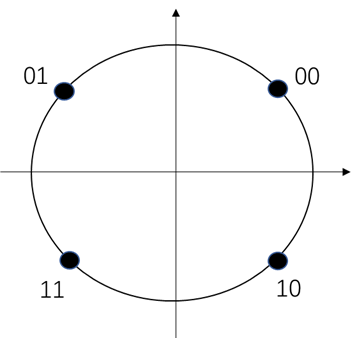
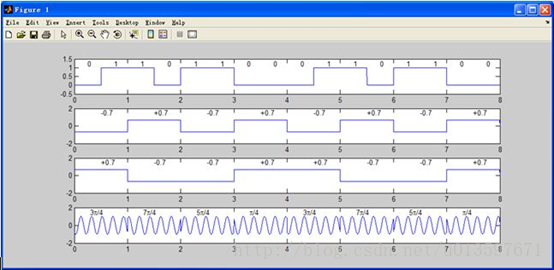
%输入信号
>>subplot(4,1,1);
>> t=0:0.001:8;
>> d=[0 0 ;0.5 1;1 1;1.5 0;2 1;2.5 1;3 0;3.5 0;4 0;4.5 1 ;5 1 ;5.5 0 ;6 1 ;6.5 1 ;7 0 ;7.5 0];
>> s=pulstran(t-0.25,d,'rectpuls',0.5);plot(t,s) ;
>> axis([0 8 -0.5 1.5]);
>> text(0.25,1.2,'0') ;text(0.75,1.2,'1') ; text(1.25,1.2,'1') ; text(1.75,1.2,'0') ;
>> text(2.25,1.2,'1'); text(2.75,1.2,'1') ; text(3.25,1.2,'0') ; text(3.75,1.2,'0') ;
>> text(4.25,1.2,'0'); text(4.75,1.2,'1') ; text(5.25,1.2,'1') ; text(5.75,1.2,'0') ;
>> text(6.25,1.2,'1'); text(6.75,1.2,'1') ; text(7.25,1.2,'0') ; text(7.75,1.2,'0') ;
% I路信号
>> subplot(4,1,2);
>> t=0:0.001:8;
>> a=1/sqrt(2);
>> d=[0 -a ;1 +a;2 -a;3 +a; 4 -a;5 +a;6 -a;7 +a];
>> s=pulstran(t-0.5,d,'rectpuls');plot(t,s) ;
>> axis([0 8 -2 2]);
>> text(0.5,1.5,'-0.7') ; text(1.5,1.5,'+0.7') ;text(2.5,1.5,'-0.7') ;text(3.5,1.5,'+0.7');
>> text(4.5,1.5,'-0.7') ; text(5.5,1.5,'+0.7') ;text(6.5,1.5,'-0.7') ;text(7.5,1.5,'+0.7');
% Q路信号
>> subplot(4,1,3);
>> t=0:0.001:8;
>> d=[0 +a;1 -a;2 -a;3 +a; 4 +a;5 -a;6 -a;7 +a];
>> s=pulstran(t-0.5,d,'rectpuls');plot(t,s) ;
>> axis([0 8 -2 2]);
>> text(0.5,1.5,'+0.7'); text(1.5,1.5,'-0.7') ; text(2.5,1.5,'-0.7') ; text(3.5,1.5,'+0.7')
>> text(4.5,1.5,'+0.7'); text(5.5,1.5,'-0.7') ; text(6.5,1.5,'-0.7') ; text(7.5,1.5,'+0.7')
%QPSK调制信号
>> subplot(4,1,4);
>> t=0:0.001:8;
>> d1=[0 -a ;1 +a;2 -a;3 +a; 4 -a ;5 +a;6 -a;7 +a];
>> s1=pulstran(t-0.5,d1,'rectpuls').*cos(2*pi*5*t);
>> d2=[0 +a;1 -a;2 -a;3 +a; 4 +a;5 -a;6 -a;7 +a];
>> s2=pulstran(t-0.5,d2,'rectpuls').*sin(2*pi*5*t);
>> plot(t,s1-s2) ;>> axis([0 8 -2 2]);
>> text(0.3,1.5,'3pi/4') ; text(1.3,1.5, '7pi/4') ; text(2.3,1.5,'5pi/4') ; text(3.3,1.5,'pi/4') ;
>> text(4.3,1.5, '3pi/4') ; text(5.3,1.5, '7pi/4');
text(6.3,1.5,'5pi/4') ; text(7.3,1.5,'pi/4') ;QPSK的映射关系可以随意定吗?
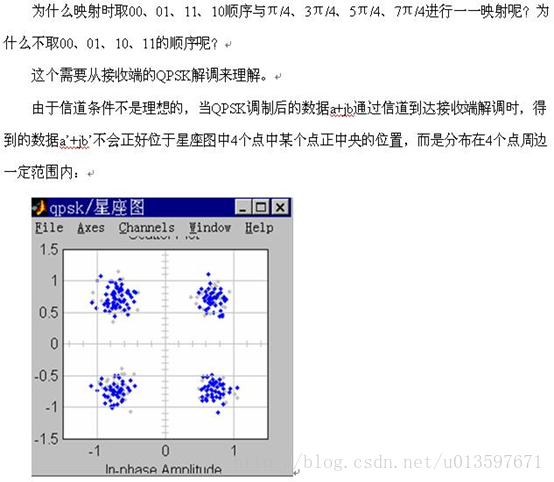
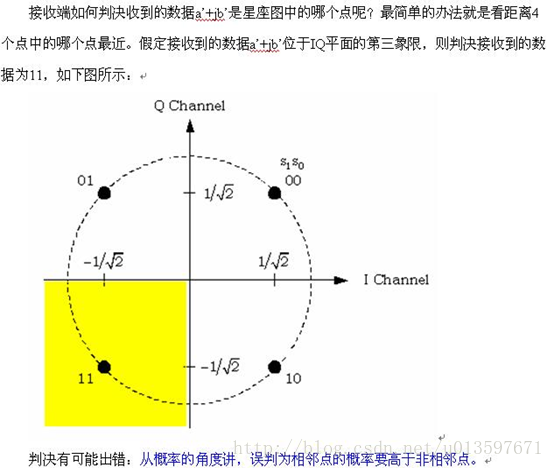
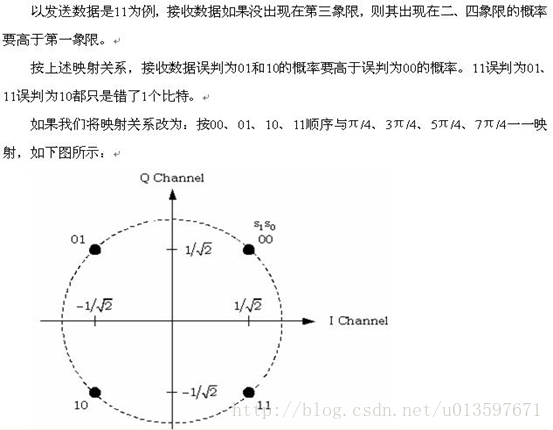
还以发送数据是11为例,接收数据误判为10和00的概率要高于误判为01的概率。11误判为10错了1个比特,但11误判为00却错了2个比特。 综上所述,在相同的信道条件下,采用00↔π/4、01↔3π/4、10↔5π/4、11↔7π/4映射关系的QPSK调制的误比特率要高于采用00↔π/4、01↔3π/4、11↔5π/4、10↔7π/4映射关系。 象00、01、11、10这样,相邻的两个码之间只有1位数字不同的编码叫做格雷码。QPSK调制中使用的就是格雷码。
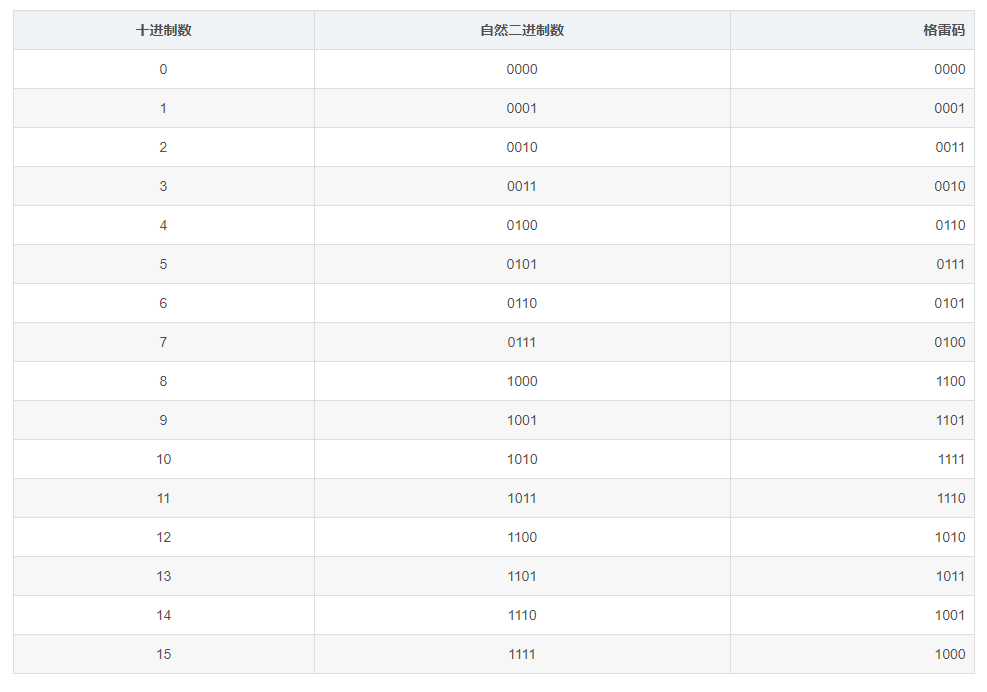
2.2 用IQ调制实现8PSK调制
在上面分析QPSK调制星座图的特征时,我们发现:发射信号点都是在单位圆的1/4位置,那么同理,对于8PSK,发射信号点都是在单位圆的1/8位置处。
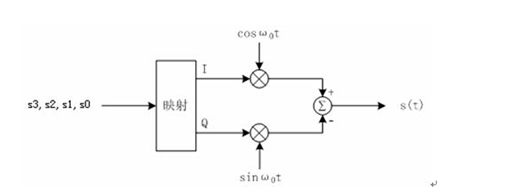
这里知道信号点在单位圆的1/8位置处,间隔为(2*pi)/8,依次增加。按照下图中的IQ信号,带入![]() ,运用和差化积公式都可转化为s(t)=cos(wt+θ)
,运用和差化积公式都可转化为s(t)=cos(wt+θ)
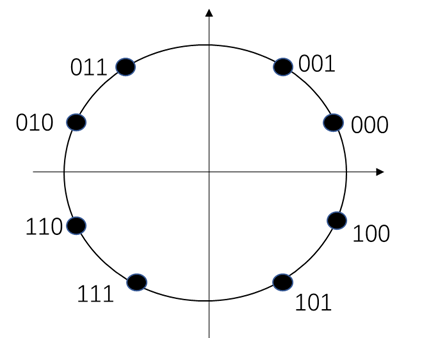
输入信号被划分为3个比特一组,如果我们按照下面的对应关系,就可以得到星座图了:

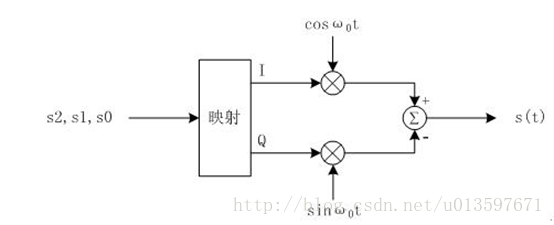
下图是8PSK调制的星座图:
三. QAM调制与IQ调制的关系
本节的学习中,我们想通过QAM的矩形星座图分析星座图的结构:
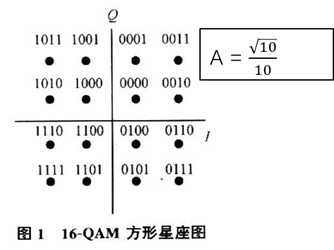
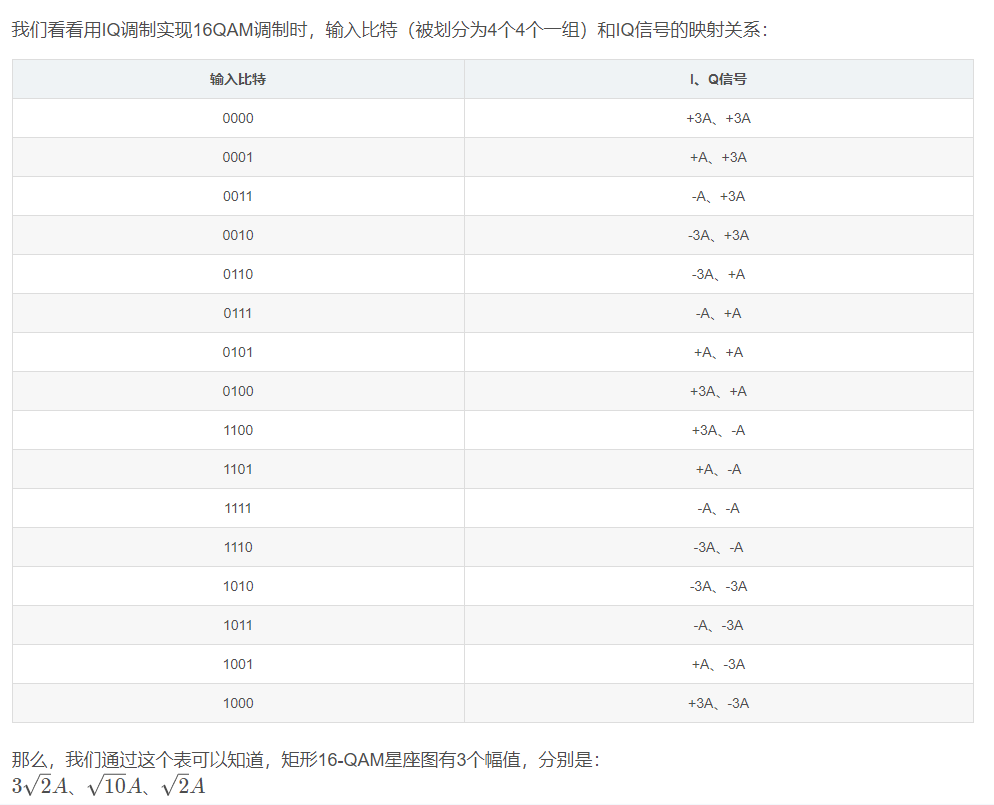
当然,我们通过矩形星座图也能够一目了然:
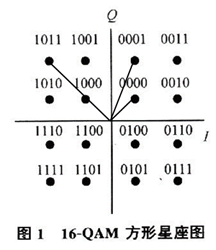
注意:对于16QAM调制,我们不是将4个bit划分为一组吗,那么它们在输入后“兵分两路”时,是把这4个bit分两路,一路2个bit,分别给I和Q,这样,I路就会有2^2 = 4个不同幅度的电平、Q路也会有4个不同幅度的电平,又由于I,Q信号正交(互不相关),因此任意一个I的幅度和任意一个Q幅度的组合都会对应一个星座点。一共就会有4x4 = 16种组合状态
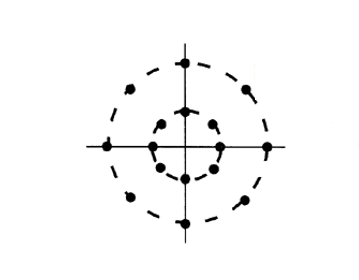
16QAM星座图不仅有上述的方形星座图,还有其它类型的,例如:圆形星座图:
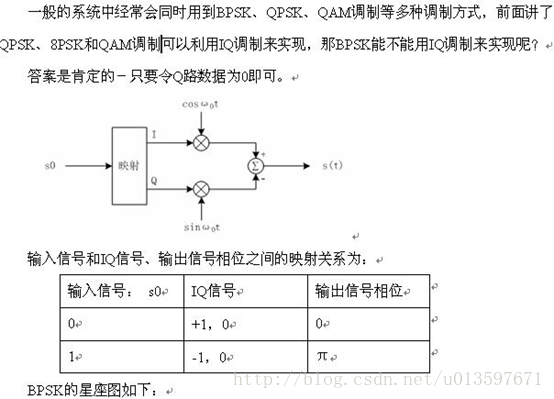
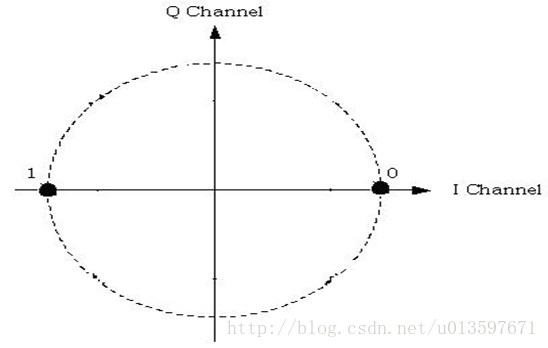
利用IQ调制实现BPSK调制
最后
以上就是孤独店员最近收集整理的关于星座图再学习 二.PSK(相移键控)和IQ调制的关系: 三. QAM调制与IQ调制的关系的全部内容,更多相关星座图再学习 二.PSK(相移键控)和IQ调制的关系: 三.内容请搜索靠谱客的其他文章。








发表评论 取消回复