Matlab使用ode45求解器求解常微分方程引言实例参考文献

110 阅读 0 评论 73 点赞

我是靠谱客的博主细心溪流，这篇文章主要介绍Matlab使用ode45求解器求解常微分方程引言实例参考文献，现在分享给大家，希望可以做个参考。

引言

ode的全称是Ordinary differential equations(常微分方程）的缩写。

ode45就是一种常微分方程求解器，这种求解器采用的是Runge-Kutta解法的中阶解法；

ode45即Nonstiff（非刚性问题）微分方程式。

注意：大部分情况下，都需要先把高阶微分方程变换成一阶微分方程组的形式进行求解。

这也解释了现代控制理论建立在状态空间方程上的原因。

假设要解下面这个微分防方程：

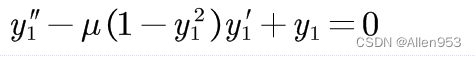
我们把这个Second order differential equation(二阶微分方程）改写乘一阶微分方程组的形式。

令

则。

ode45这个微分方程求解器的用法如下：

我们编写如下代码，把微分方程写出来。

这里的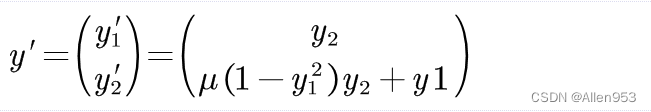

我们令为1，所以

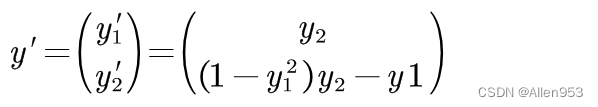
写成代码即为如下所示：

复制代码

1
2
3
4
5
function dy = odeBai(t,y)
dy = zeros(2,1);
dy(1) = y(2);
dy(2) = (1 - y(1) * y(1)) * y(2) - y(1);
end

matlab代码

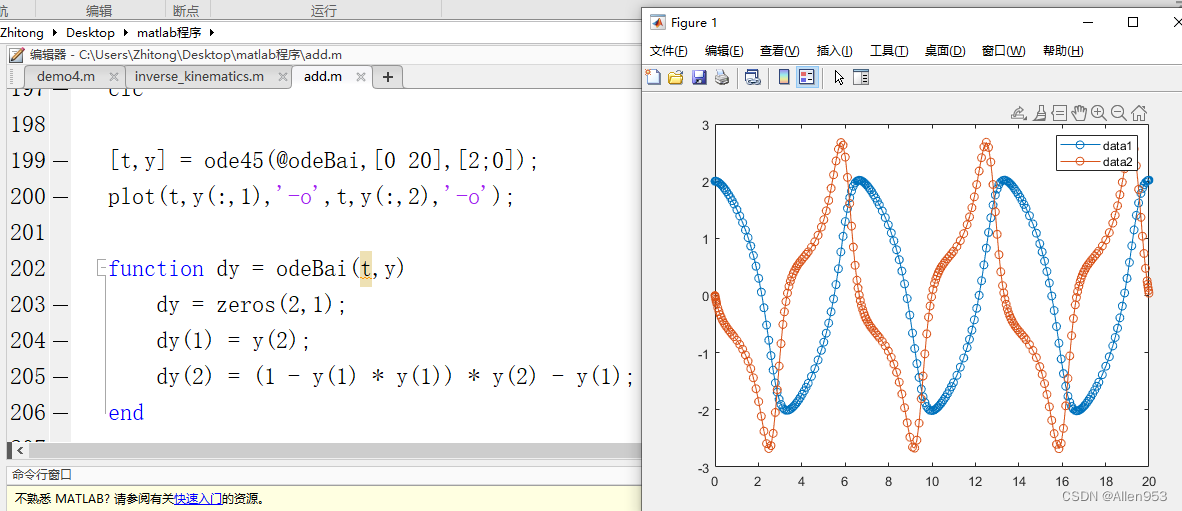
然后就调用求解器求解这个微分方程：

复制代码

1
[t,y] = ode45(@odefun,[0 20],[2; 0]);

第二个参数是仿真时间范围，就是从0秒到20秒。

第三个参数是状态初值，即初始时间dy=2，ddy=0；

1.matlab帮助文档

本图文内容来源于网友提供，作为学习参考使用，或来自网络收集整理，版权属于原作者所有。