1、常微分方程（Lorenze混沌系统）：
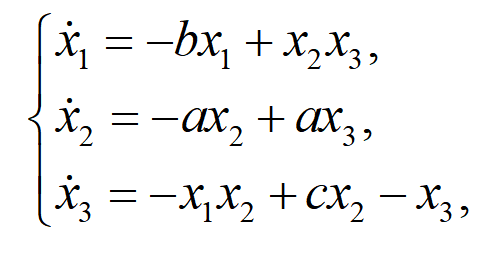
方法1：m文件实现
复制代码
1
2
3
4
5
6
7function exam1 x0=[0;0;1e-3]; [t,x]=ode45(@lorenzfun,[0,100],x0); figure(1) plot(t,x) figure(2) plot3(x(:,1),x(:,2),x(:,3))
复制代码
1
2
3
4
5
6function dx=lorenzfun(t,x) a=10;c=28;b=8/3; dx=zeros(3,1); dx(1)=-b*x(1)+x(2)*x(3); dx(2)=-a*x(2)+10*x(3); dx(3)=-x(1)*x(2)+c*x(2)-x(3);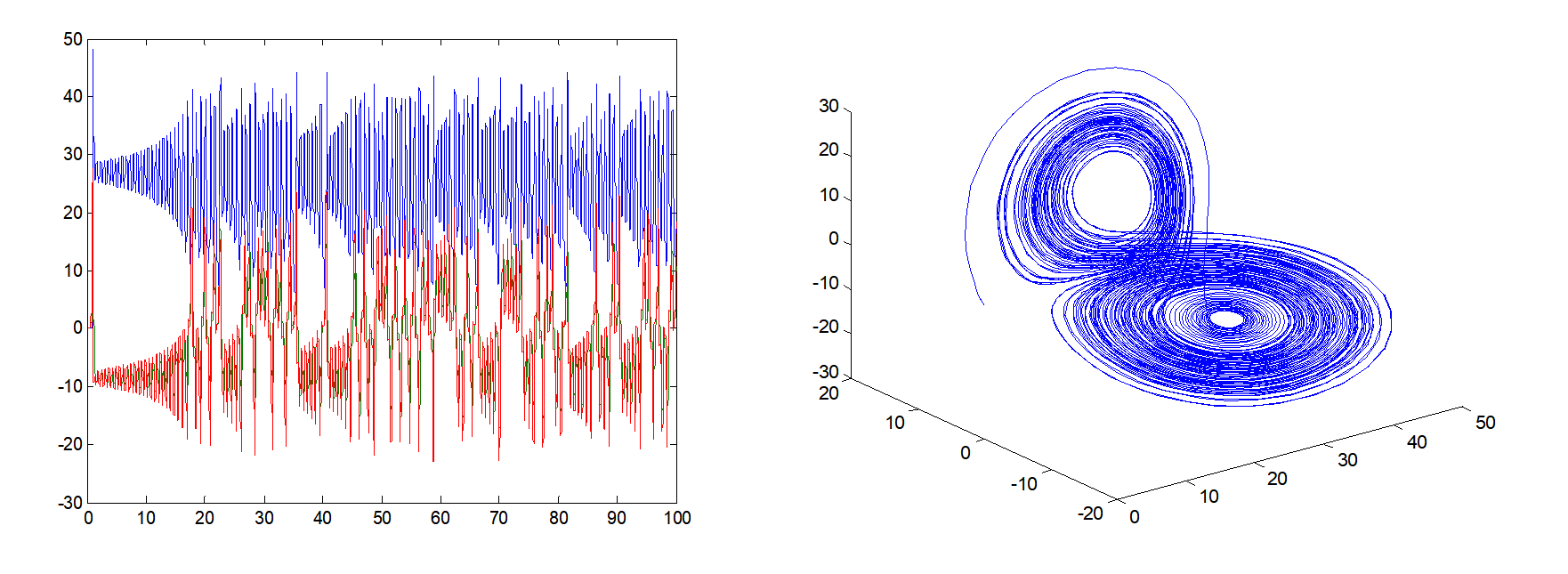
方法2：Simulink模糊实现
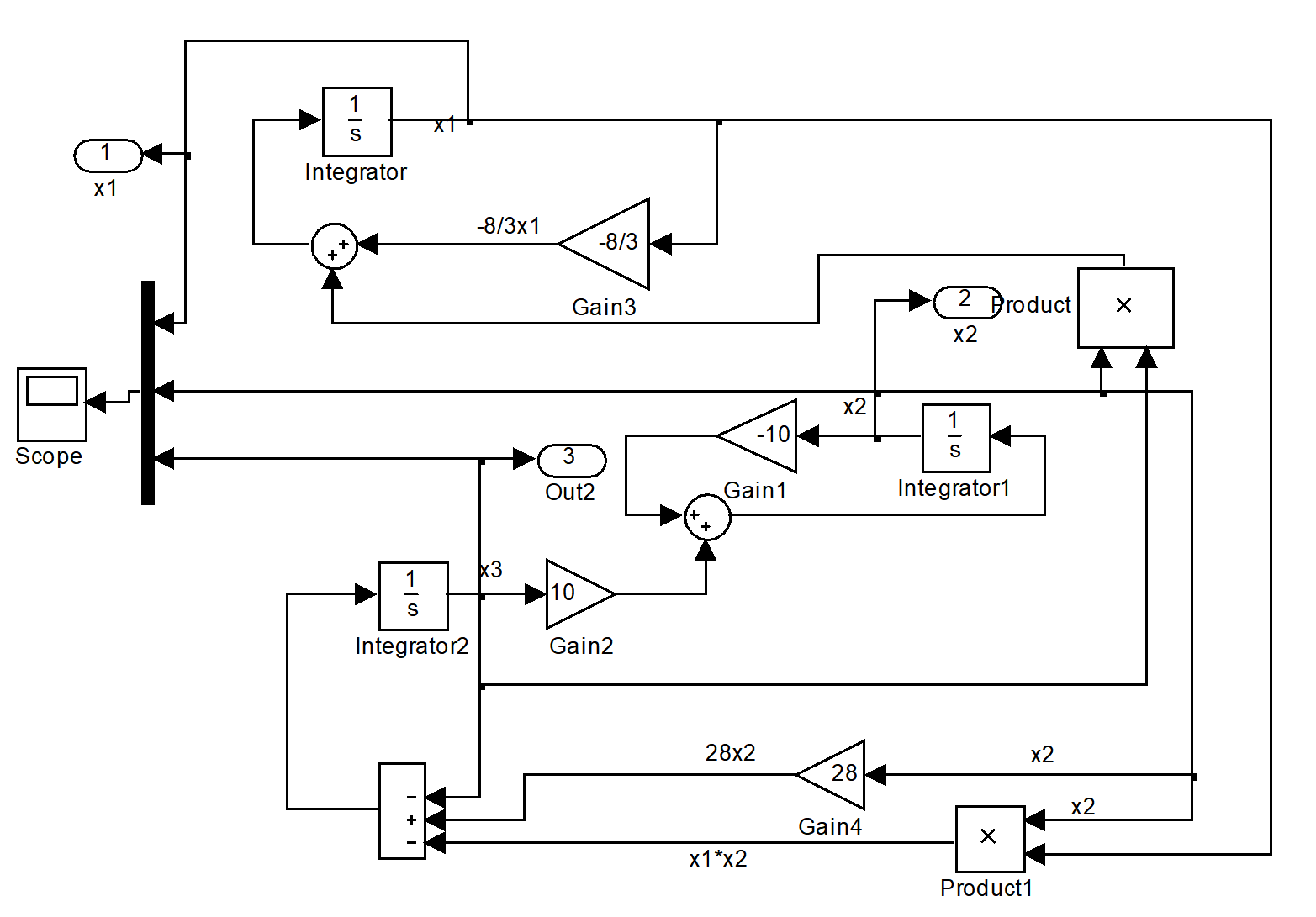
其中三个积分模块的初始值设置与exam1相同，仿真时长为100s。精度设置：Simulation--Configuration Parameters—Relative tolerance, 1e-3改为1e-5（试试不作此修改的结果比较）。运行后双击示波器scope后可看到：
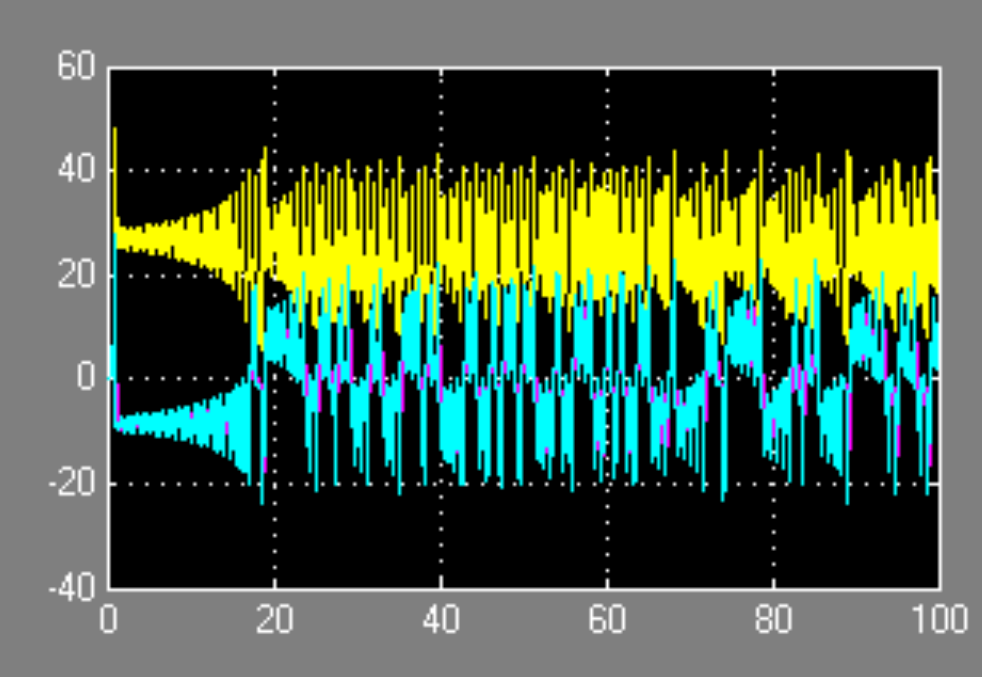
在matlab命令窗口输入画图命令：
复制代码
1
2
3
4figure plot(tout,yout) figure plot3(yout(:,2),yout(:,3),yout(:,1))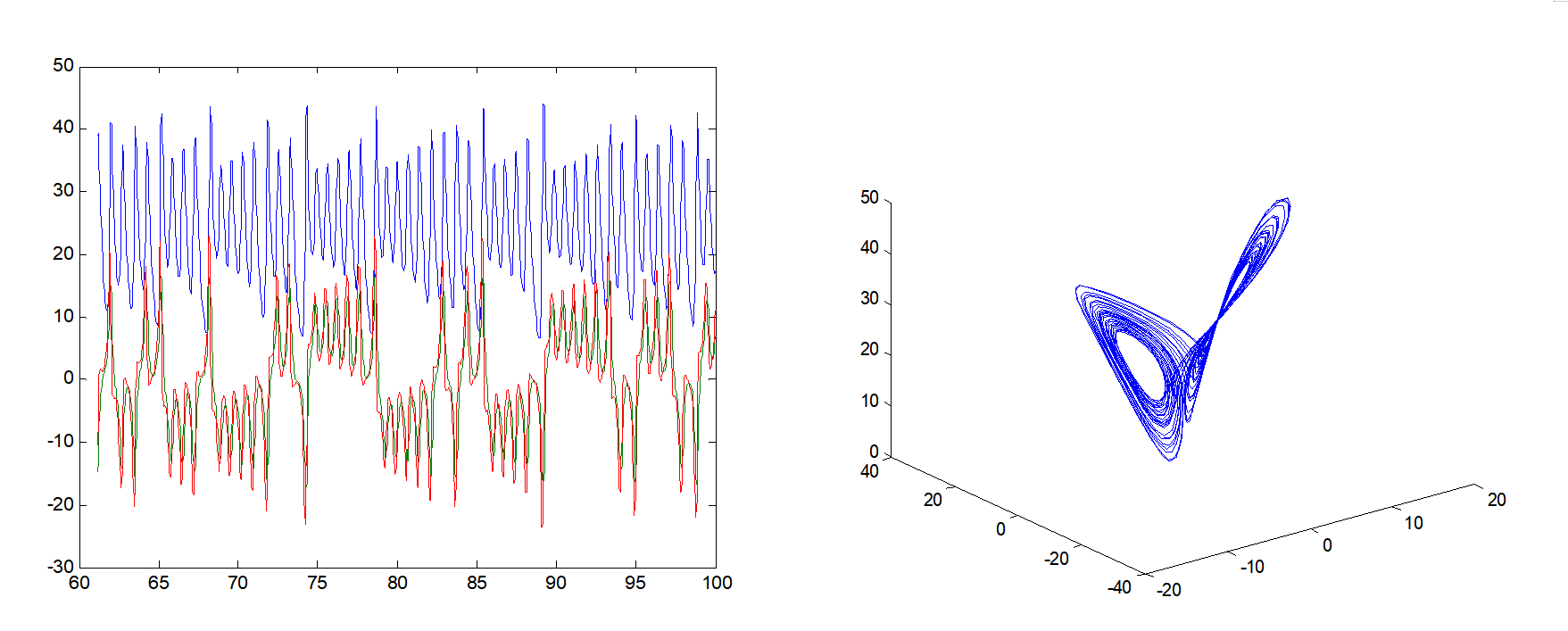
方法3：simulink向量模块
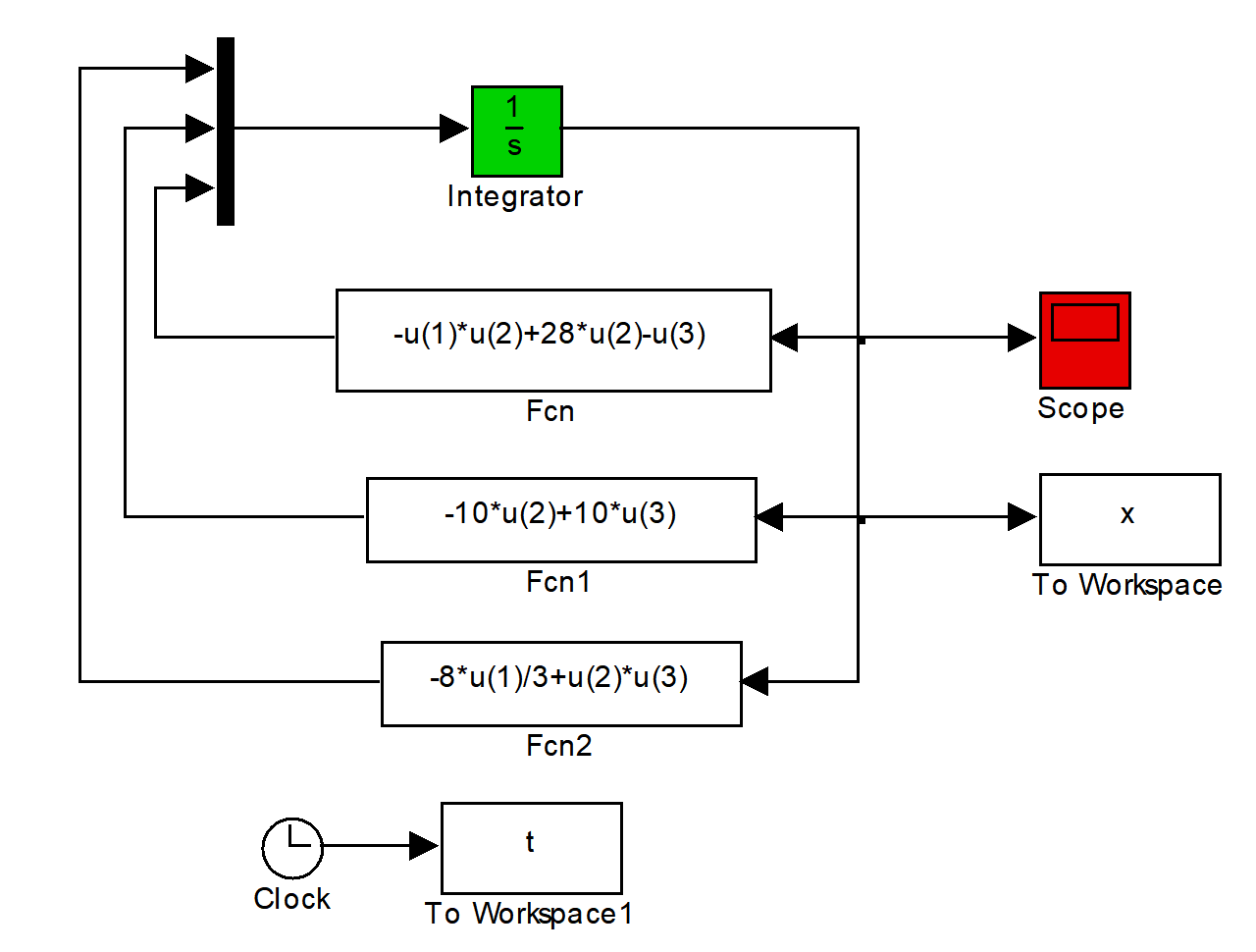
方法4：Simulink中S函数的实现
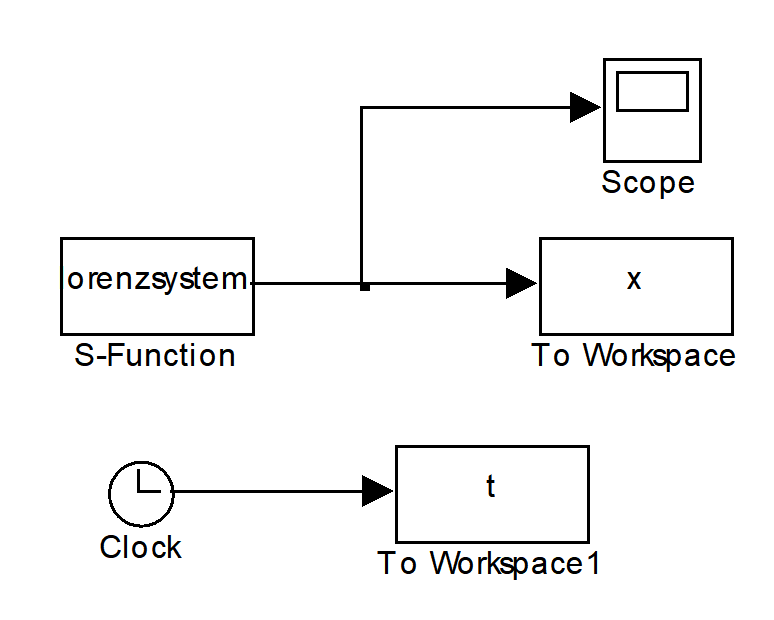
2、常时滞微分方程
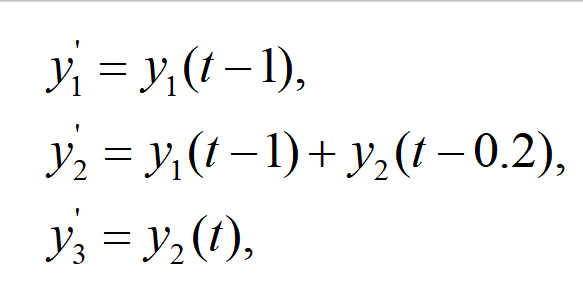
方法1：m文件需调用dde23来求解
复制代码
1
2
3
4
5
6function exam2 sol = dde23('exam1f',[1, 0.2],ones(3,1),[0, 5]); plot(sol.x,sol.y); title('Example 2') xlabel('time t'); ylabel('y(t)');
复制代码
1
2
3
4
5
6
7function v = exam1f(t,y,Z) ylag1 = Z(:,1); ylag2 = Z(:,2); v = zeros(3,1); v(1) = ylag1(1); v(2) = ylag1(1) + ylag2(2); v(3) = y(2);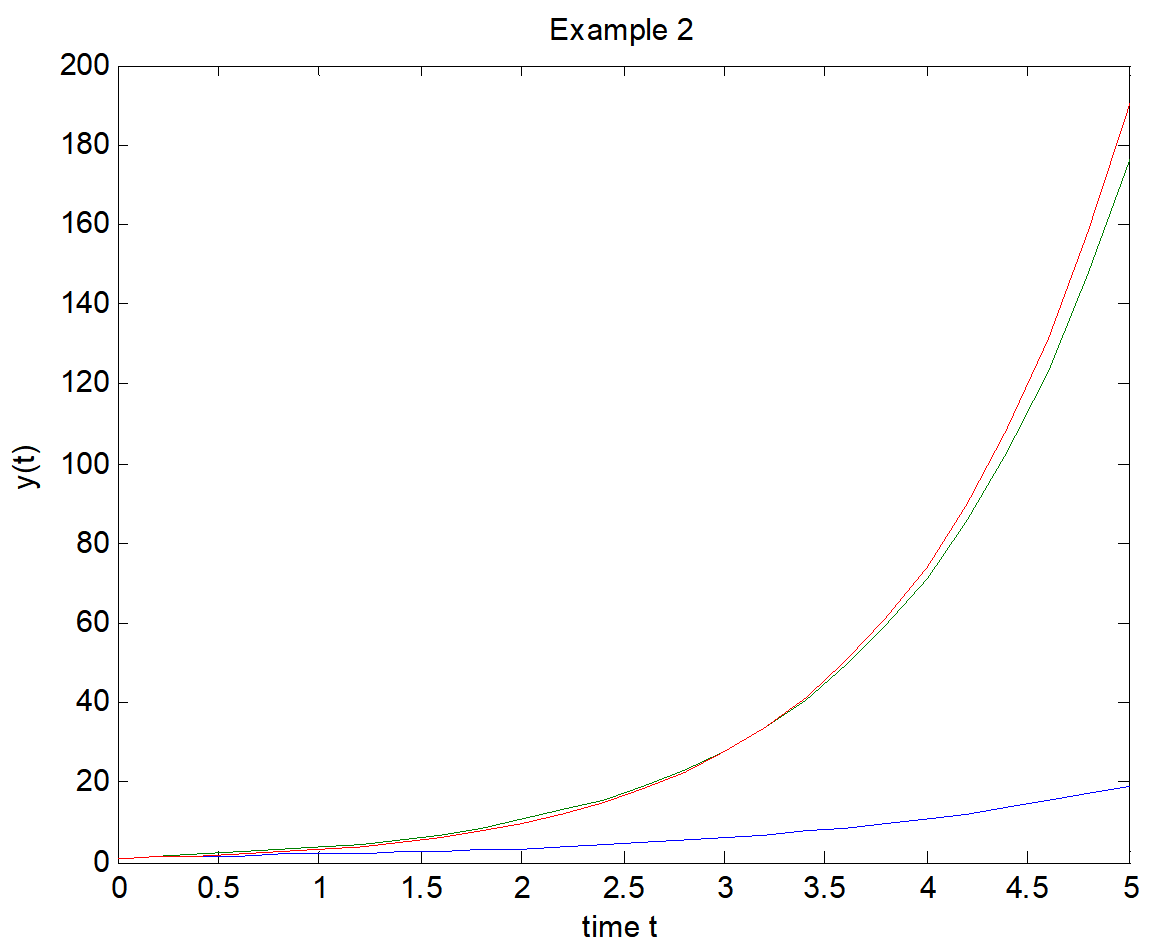
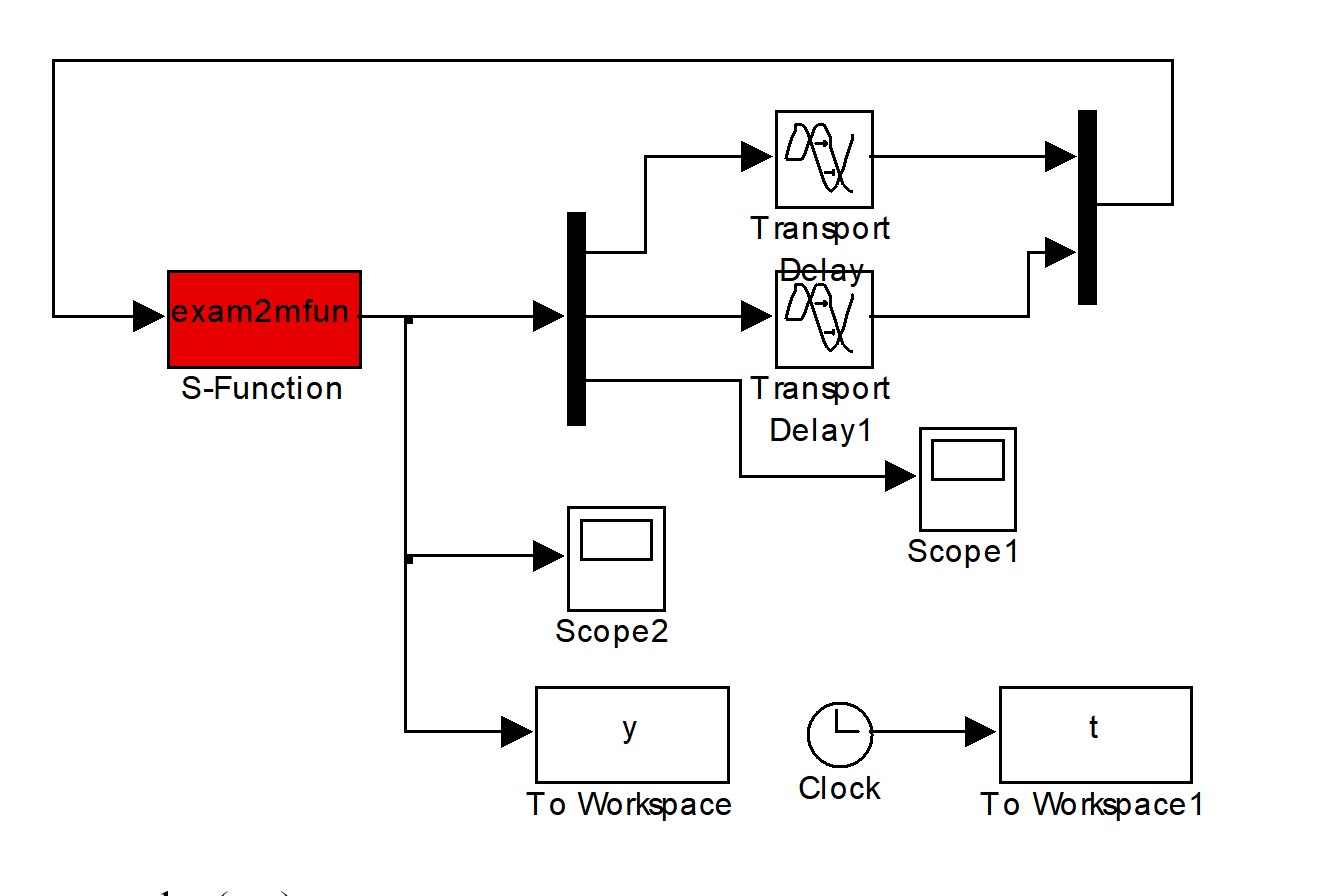
方法2：Simulink中S函数来实现：
注：用Simulink中S函数求解时滞微分方程的核心思想在于：将时滞变量作为S函数的外部输入。
最后
以上就是背后保温杯最近收集整理的关于matlab simulink 求解连续微分系统 混沌系统的全部内容，更多相关matlab内容请搜索靠谱客的其他文章。
本图文内容来源于网友提供，作为学习参考使用，或来自网络收集整理，版权属于原作者所有。
发表评论 取消回复