一元微分方程

在使用ode45函数时，要先把方程变形一下。
比如方程$$\ddot{x}\left(t\right)+\dot{x}\left(t\right)+x\left(t\right)=0$$需要像化成状态方程一样化成$$\ddot{x}\left(t\right)=-\dot{x}\left(t\right)-x\left(t\right)$$ $$x\left(t\right)=x_1$$ $$\dot{x}=x_2$$则$$\ddot{x}=-x_2-x_1$$这样在构建function时就比较明了，function构造如下

function dx = myfunc(t,x)
%方程为d2x+dx+x=0
%将其转化为类似状态方程的模型为d2x=-dx-x
%令x=x1,dx=x2
%函数的输入参数为x1和x2的初始值，即x和dx的初始值
dx = zeros(2,1);%dx(1)为dx/dt,dx(2)=d2x/dt2
%dx(1)为当x2传进来之后，计算的下一个步长的x2,dx(2)相当于根据dx(1)和x1算出的d2x
dx(1) = x(2);%x(2) = dx/dt,相当于x2
dx(2) = -dx(1)-x(1);%x(1)是x,相当于x1

输入参数x为x和dx的第一个值（初值），这个数的大小是与ode45的第三个参数决定的，是与他一样的大小。并且含义都是一样的。
dx这里定义为一个初值为0的2维的向量，dx(1)为dx，dx(2)为d2x。这样就可以根据输入的初值进行迭代更新了。
利用另外一个脚本来调用这个函数

t = (0:0.01:10)';
[t,y] = ode45('myfunc',t,[1; 0]);%1是x的初值，0是dx的初值
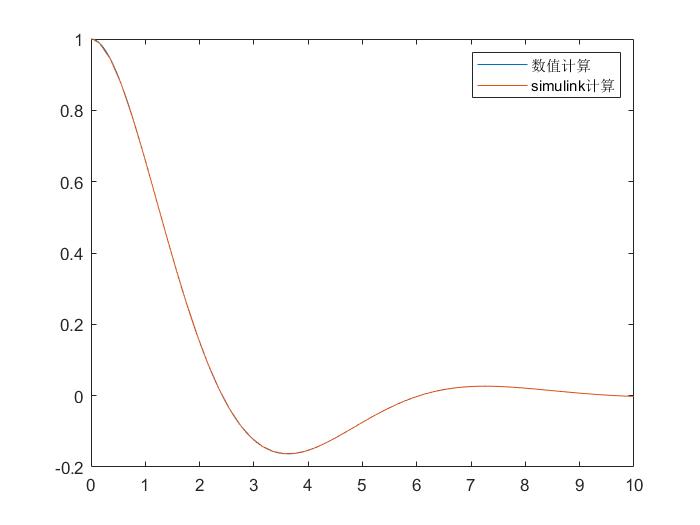
plot(t,y(:,1),out.tout,out.simout)
legend('数值计算','simulink计算')

这里我用simulink的模块也搭建了相同的微分方程，结果基本是相同的。

二元微分方程

这里我随便写了一个二元微分方程如下$${\ddot{x}}_1\left(t\right)+{\dot{x}}_1\left(t\right)+x_2\left(t\right)=0$$$${\ddot{x}}_2\left(t\right)+{\dot{x}}_1\left(t\right)+x_1\left(t\right)=0$$将其变形得$$X_1=x_1$$$$X_2={\dot{x}}_1$$$$X_3=-{\dot{x}}_1-x_2$$$$Y_1=x_2$$$$Y_2={\dot{x}}_2$$$$Y_3=-{\dot{x}}_1-x_1$$连理$X_3$和$Y_3$的两个式子得

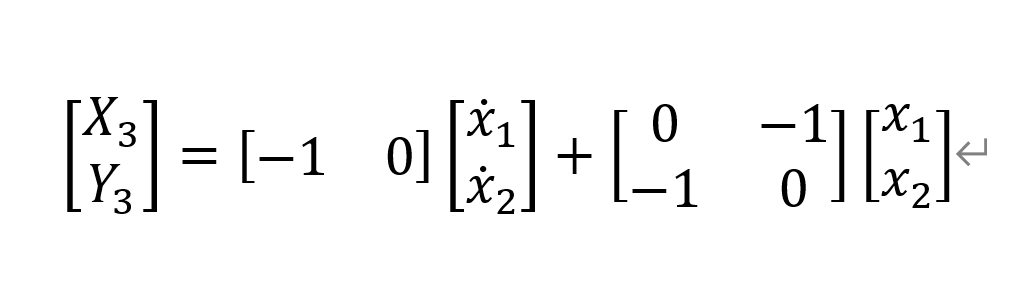
function dx = myfuncs(t,x)
dx = zeros(4,1);
A = [-1 0]; B = [0 -1; -1 0];
dx(1:2) = x(3:4);
dx(3:4) = A*dx(1:2)+B*x(1:2);

这里定义的dx前两个为dx1/dt和dx2/dt，后两个定义的是d2x1/dt和d2x2
x输入进来的向量的前两个是x1和x2，后两个为dx1/dt和dx2/dt
所以这里输入常数矩阵之后，第一步做的就是通过x里面的dx1/dt和dx2/dt更新dx的dx1/dt和dx2/dt，第二步更新加速度也就是dx后两个变量，这里是用dx(3:4)

t = (0:0.01:10)';
[t,y] = ode45('myfuncs',t,[1; 0; 0; 0]);
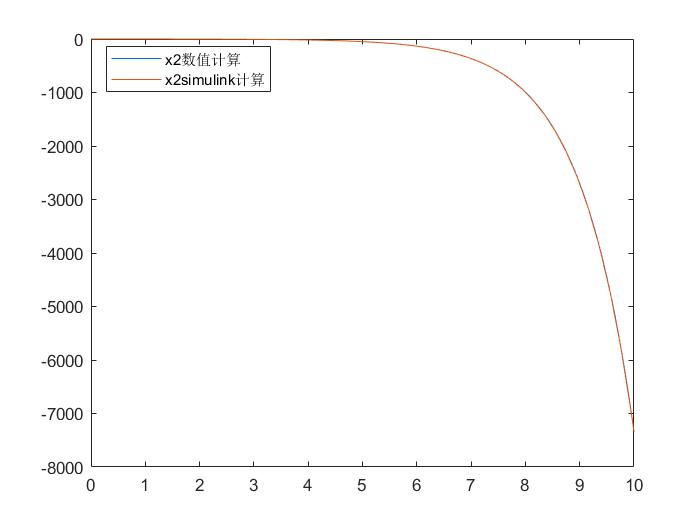
plot(t,y(:,1),out.tout,out.simout1)
legend('数值计算','simulink计算')
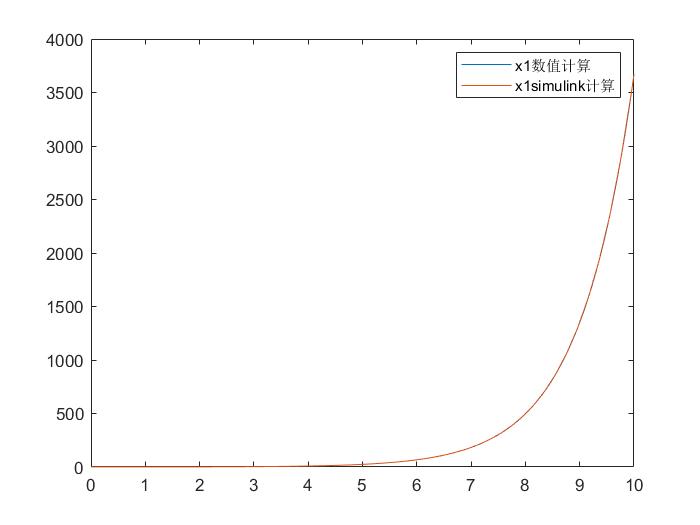
plot(t,y(:,2),out.tout,out.simout2)
legend('数值计算','simulink计算')

对比结果如下

最后

以上就是专一小蝴蝶为你收集整理的matlab ode45的使用一元微分方程二元微分方程的全部内容，希望文章能够帮你解决matlab ode45的使用一元微分方程二元微分方程所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。