引言

写这篇博客目的是自己在求解微分方程的时候，考虑到 ode45() 可能求解速度比较慢，想用一种快速一点的微分方程求解算法，又想到 ode45() 用的就是 Runge-Kutta （RK）算法，所以想是不是自己可以自己编写一个 RK 算法用来代替 ode45()。因为 MATLAB 的 ode45() 算法中可能存在较多的判断条件，这也许是让 ode45() 速度较慢的一个原因，而自己编写的 RK 算法省略了很多不必要的判断，也许会快一些。

ode45()

ode45() 算法是 MATLAB 中专门用于求解常微分方程（Ordinary differential equations，ODE）的函数，它在求解微分方程时的步长是变步长的，使用也是 RK 算法。

45 代表了 ode45() 使用 4 阶- 5阶 RK 算法。其中，4 阶方法用于提供 ODE 的候选解，5 阶方法用于控制误差，整体截断误差为 $\Delta x^5$。

Runge-Kutta 算法

RK 算法是德国数学家 Runge 和 Kutta 在 1900 年前后提出的一种高精度求解微分方程的数值算法。该算法间接使用 Taylor 级数展开构造高精度数值方法，利用函数 $f$ 在若干点的值的线性组合代替 $f$ 的导数，再利用 Taylor 级数展开方法确定其中系数。

下面详细说明 RK 算法如何求解一阶微分方程。

对于如下问题：

$$\{\begin{array}{c}\begin{array}{rl}& \dot{\mathbf{y}}=f(t,\mathbf{y}),\\ & \mathbf{y}(t_0)={\mathbf{y}}_0,\end{array}\end{array}$$

式中，$t_0$ 为初始时间，${\mathbf{y}}_0$ 为初始状态，$f(t,\mathbf{y})$ 为关于时间 $t$ 和状态 $\mathbf{t}$ 的函数。

那么 4 阶 RK 算法为：

$$\{\begin{array}{c}\begin{array}{rl}& k_1=f(t(k),\mathbf{y}(k)),\\ & k_2=f(t(k)+h/2,\mathbf{y}(k)+k_{1}h/2),\\ & k_3=f(t(k)+h/2,\mathbf{y}(k)+k_{2}h/2),\\ & k_4=f(t(k)+h,\mathbf{y}(k)+k_{3}h),\\ & \mathbf{y}(k+1)=\mathbf{y}(k)+h(k_1+2k_2+2k_3+k_4)/6,\\ & \mathbf{y}(0)={\mathbf{y}}_0.\end{array}\end{array}$$

上式即为 $\mathbf{y}(k)$ 向 $\mathbf{y}(k+1)$ 递推的形式，根据初始条件可以求出 $\mathbf{y}(1)$，$\mathbf{y}(2)$，$\mathbf{y}(3)$，$\mathbf{y}(4)$，$\cdots$ $\mathbf{y}(N)$，该离散序列即为微分方程的数值解。

RK 算法程序

在这里给出 RK 算法的 MATLAB 程序。

%--- RK 算法 ---%
% ufunc - 微分方程组的函数名
% y0 - 初始值
% h - 步长
% a - 初始时间
% b - 末端时间
function [x,y]=runge_kutta1(ufunc,y0,h,a,b)
% 步数
n = floor((b-a)/h);
% 时间起点
x(1) = a;
% 初始值
y(:,1)=y0;
% 算法开始
for iter=1:n
% 时间变量
x(iter+1) = x(iter)+h;
% 开始迭代
k1 = ufunc(x(iter),
y(:,iter));
k2 = ufunc(x(iter) + h/2, y(:,iter) + h*k1 / 2);
k3 = ufunc(x(iter) + h/2, y(:,iter) + h*k2 / 2);
k4 = ufunc(x(iter) + h,
y(:,iter) + h*k3 );
% 得到结果
y(:,iter+1) = y(:,iter) + h * (k1 + 2*k2 + 2*k3 + k4) / 6;
end
end

仿真

用一个一阶微分方程数值求解例子来对比 ode45() 和 自编 RK 算法的效果。

对于问题

$$\{\begin{array}{c}\begin{array}{rl}{\dot{y}}_1& =y_2{y}_3,\\ {\dot{y}}_2& =-y_1+y_3,\\ {\dot{y}}_3& =-0.51y_1{y}_2,\\ \mathbf{y}& =(y_{10},y_{20},y_{30})=(1,1,3).\end{array}\end{array}$$

在时间区间 $[0,t_f]$ 上的解，其中 $t_f$ 未定。

仿真代码

给出 MATLAB 解决上述问题的仿真代码。

clc;clear;close all;
%% 主函数
% 时间变量
t0 = 0;
tf = 1000;
% 初值
y10 = 1;
y20 = 1;
y30 = 3;
y = [y10,y20,y30];
% RK 算法步长
h = 0.25;
% 对该微分方程组用ode45和自编的龙格库塔函数进行比s较，调用如下：
% ode45()函数
tic;
[T,F] = ode45(@fun,[t0 tf],y);
time_record_ode = toc;
toc;
% 自编RK函数
tic;
[T1,F1]=runge_kutta1(@fun,y,h,t0,tf);
time_record_rk = toc;
toc;
%% 画图
figure('color',[1 1 1],'position',[600,100,500*1.5,416*1.5]);
subplot(121);
plot(T,F,'LineWidth',1.5);
title(['ode45','($t_f$=',num2str(tf),')'],'Interpreter','Latex');
set(gca,'FontSize',15,'FontName','Times New Roman','LineWidth',1.5);
subplot(122);
plot(T1,F1,'LineWidth',1.5);
title(['RK4','($t_f$=',num2str(tf),'),($h$=',num2str(h),')'],'Interpreter','Latex');
set(gca,'FontSize',15,'FontName','Times New Roman','LineWidth',1.5);
% 保存数据
str = ['tf_',num2str(tf),'_h_',num2str(h),'.mat'];
str_fig = ['tf_',num2str(tf),'_h_',num2str(h),'.jpg'];
save(str);
saveas(gcf,str_fig)
%% 子函数部分
% 微分方程
function dy = fun(t,y)
dy = zeros(3,1);%初始化列向量
dy(1) = y(2) * y(3);
dy(2) = -y(1) + y(3);
dy(3) = -0.51 * y(1) * y(2);
end
%--- RK 算法 ---%
% ufunc - 微分方程组的函数名
% y0 - 初始值
% h - 步长
% a - 初始时间
% b - 末端时间
function [x,y]=runge_kutta1(ufunc,y0,h,a,b)
% 步数
n = floor((b-a)/h);
% 时间起点
x = zeros(n,1);
x(1) = a;
% 初始值
y(:,1)=y0;
% 算法开始
for iter=1:n
% 时间变量
x(iter+1) = x(iter)+h;
% 开始迭代
k1 = ufunc(x(iter),
y(:,iter));
k2 = ufunc(x(iter) + h/2, y(:,iter) + h*k1 / 2);
k3 = ufunc(x(iter) + h/2, y(:,iter) + h*k2 / 2);
k4 = ufunc(x(iter) + h,
y(:,iter) + h*k3 );
% 得到结果
y(:,iter+1) = y(:,iter) + h * (k1 + 2*k2 + 2*k3 + k4) / 6;
end
end

算法主要对比的有 2 项指标，计算精度和计算效率。

不同终端时间下的算法对比

分别对比 $t_f=15,10^2,10^3,10^4,10^5$ 时，ode45() 和 RK 算法的计算精度和计算效率。

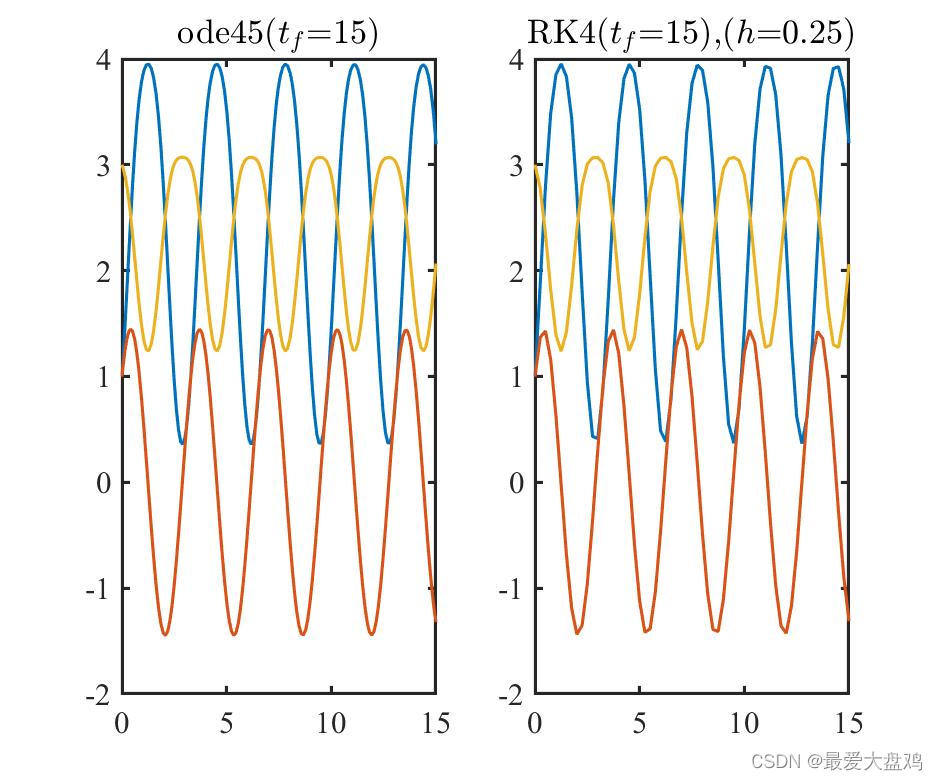
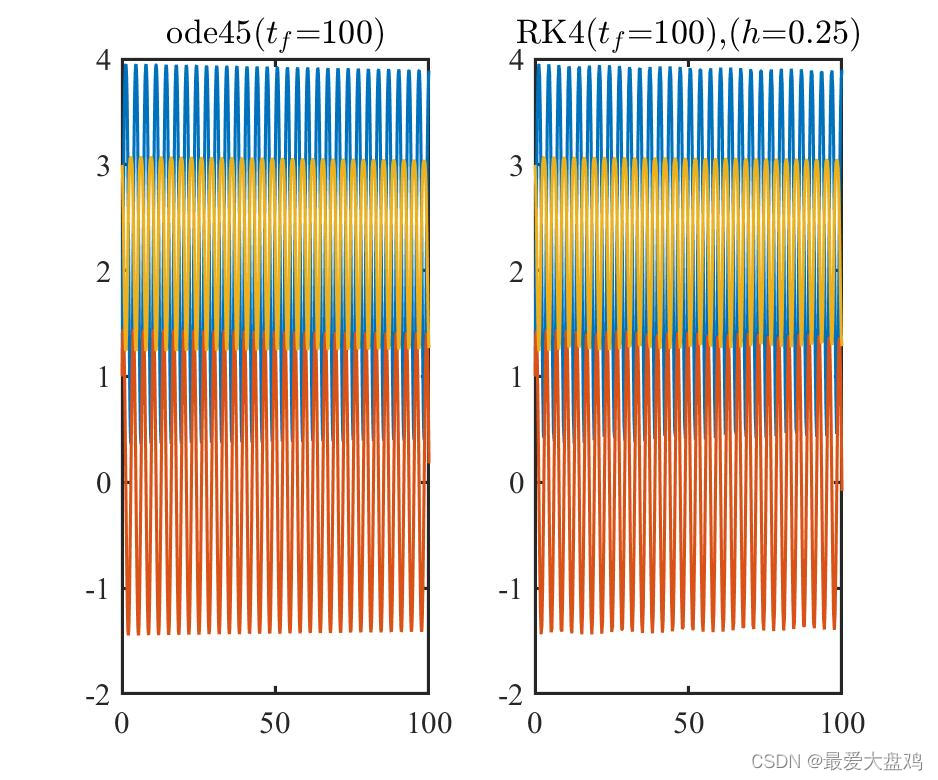
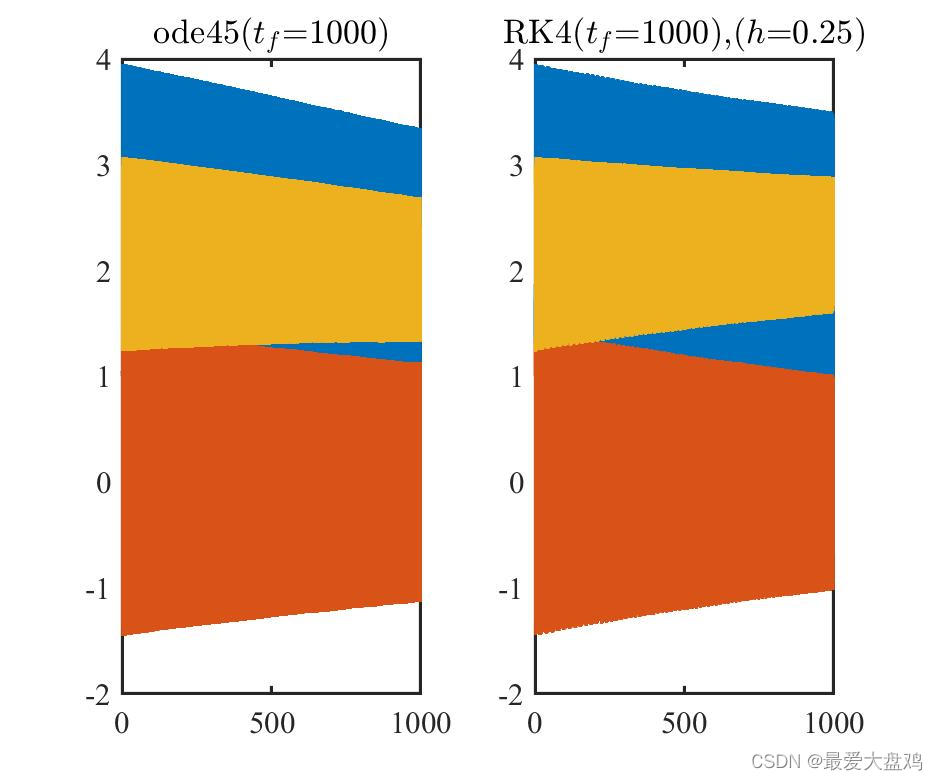
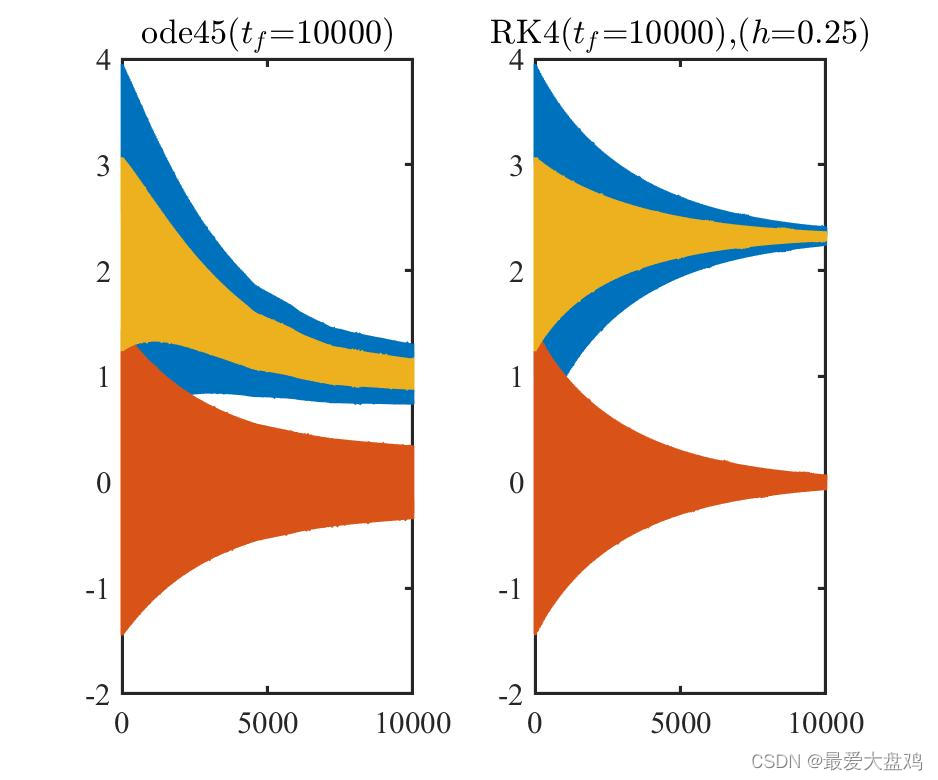
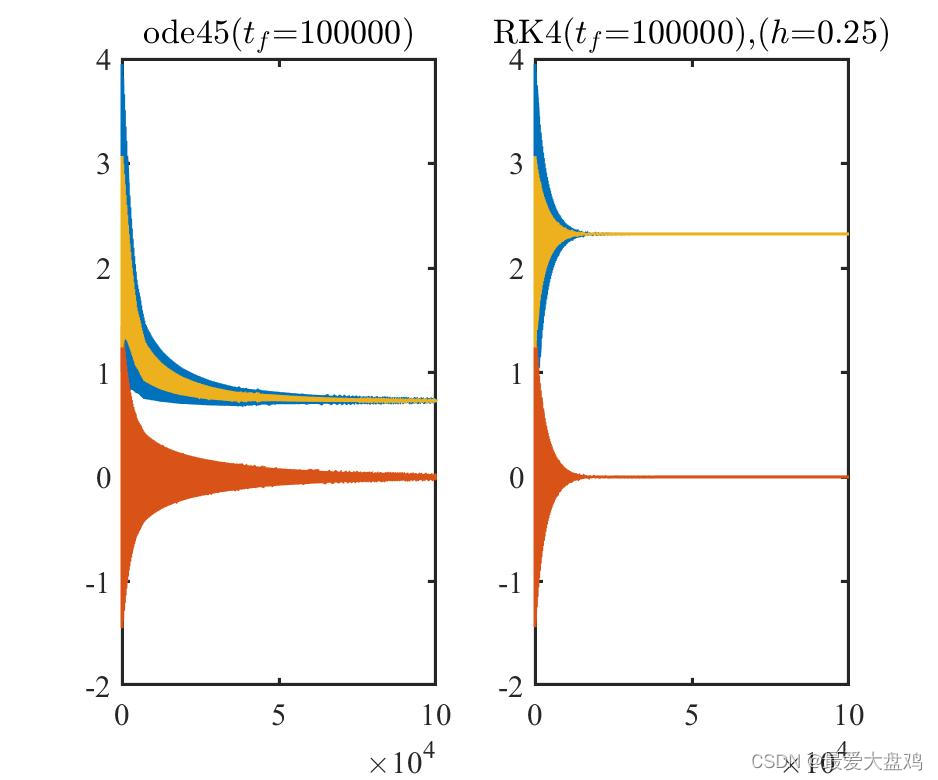
从计算精度来看，计算时间比较小的时候， RK 算法和 ode45() 的区别不是很大，但是计算时间增大之后，到了 $t_f=10^3,10^4,10^5$ 的时候，RK 算法的精度就逐渐跟不上 ode45() ，此时 RK 算法累积的误差更大一些了。

从计算效率来看，RK 算法的计算效率要优于 ode45() ，不过计算时间增大到 $t_f=10^5$ 的时候，ode45() 的计算效率超过了 RK 算法，猜想是计算时间太长，自编的 RK 算法无法针对这么长计算时间的微分方程做特定优化，所以导致计算时间慢于 ode45()。

不同步长下的算法对比

分别对比 $t_f=15$ 和 $t_f=10^3$ ，Rk 算法步长为 $h=0.01,0.10,0.20,0.25,0.35,0.50$ 时，ode45() 和 RK 算法的计算精度和计算效率。

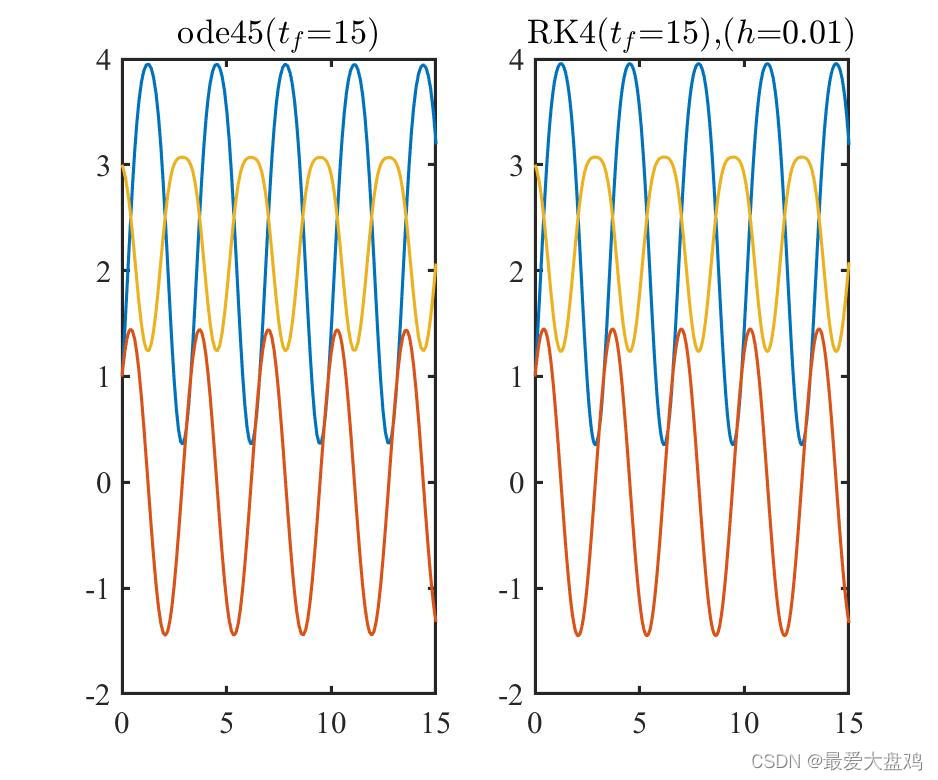
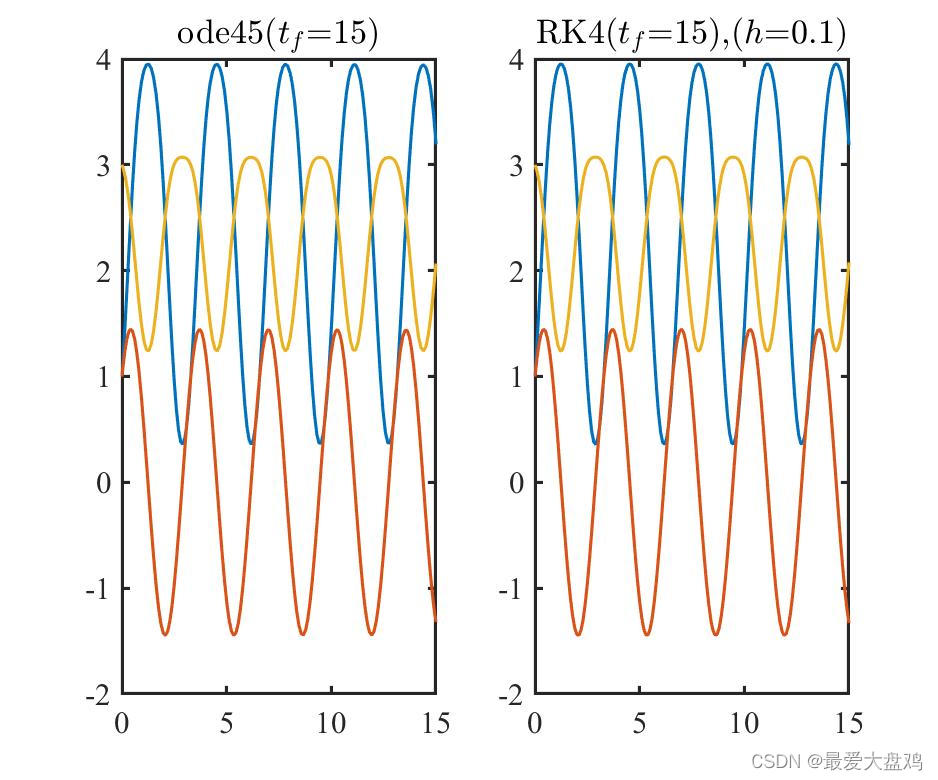
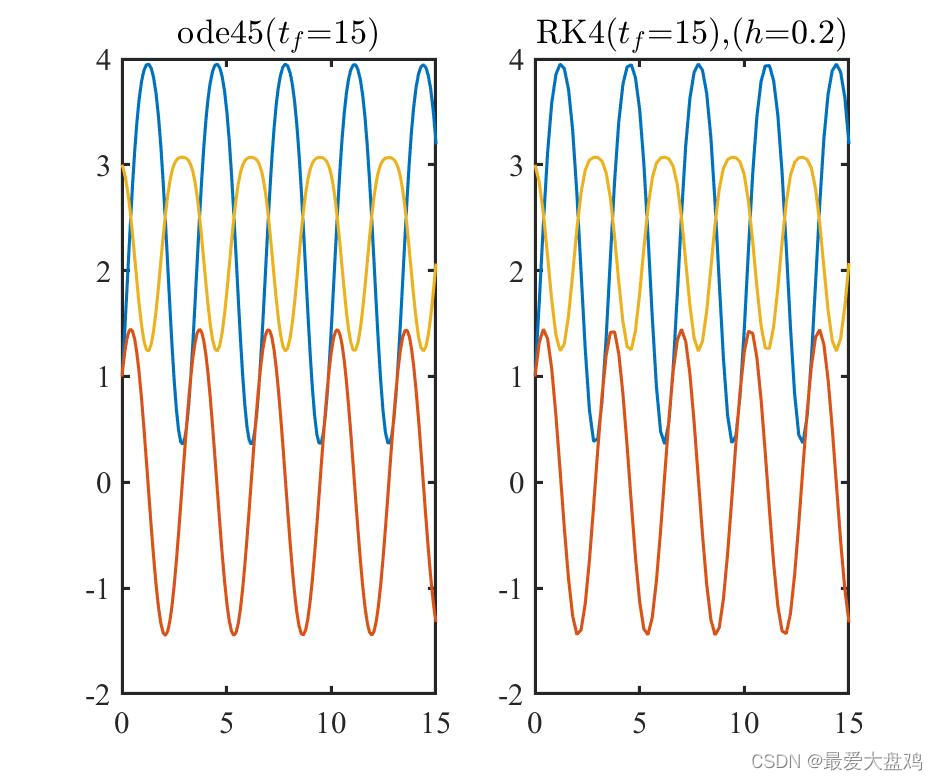
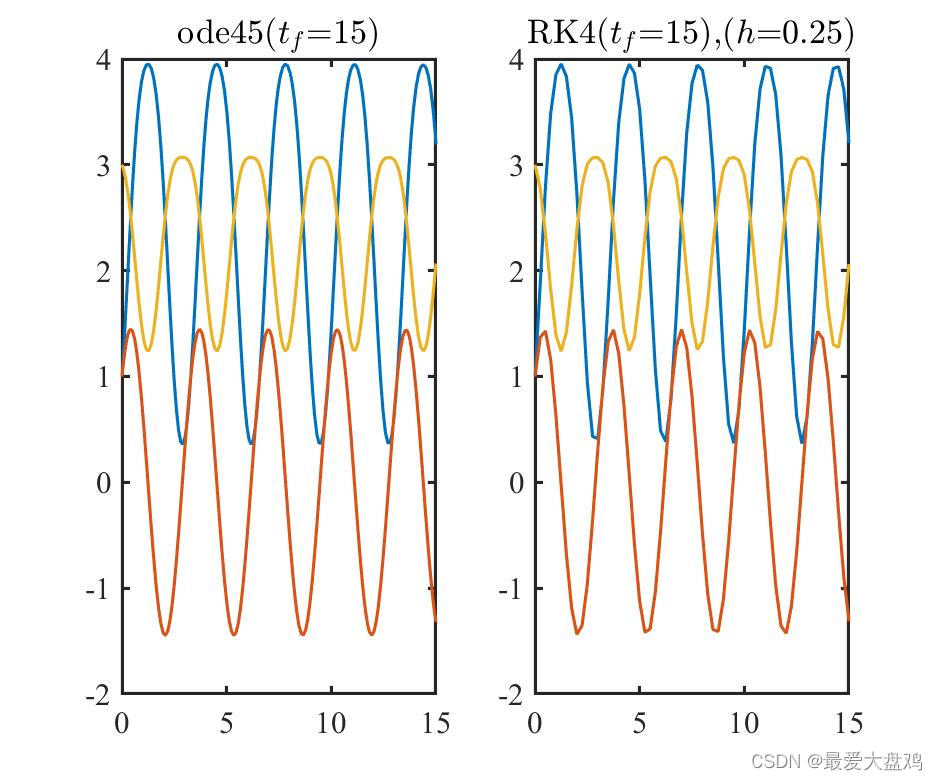
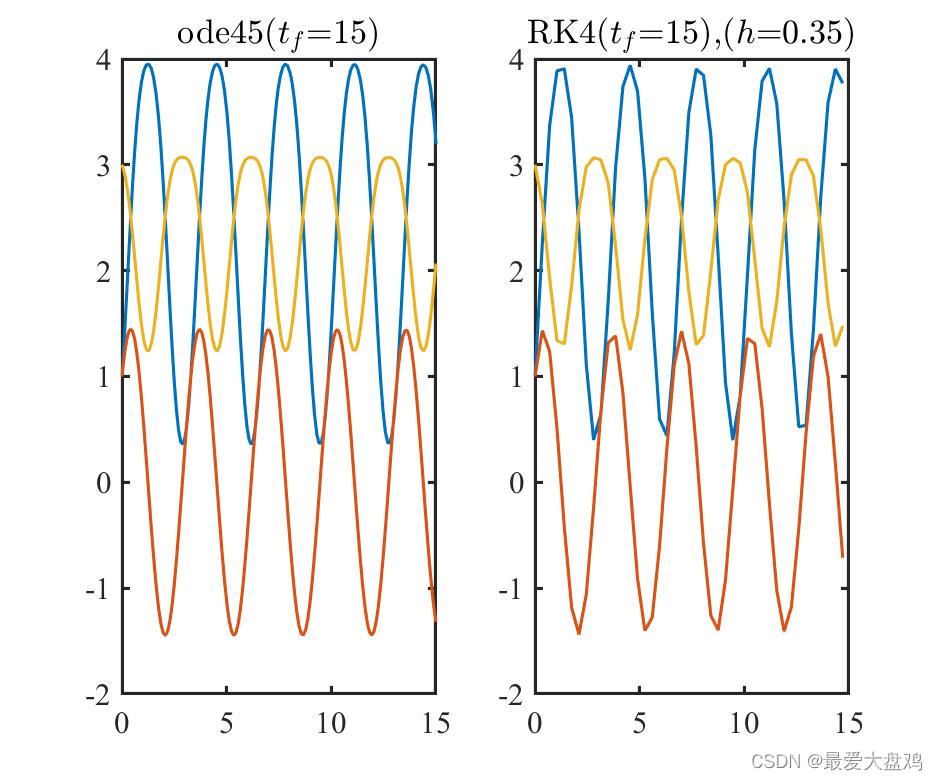
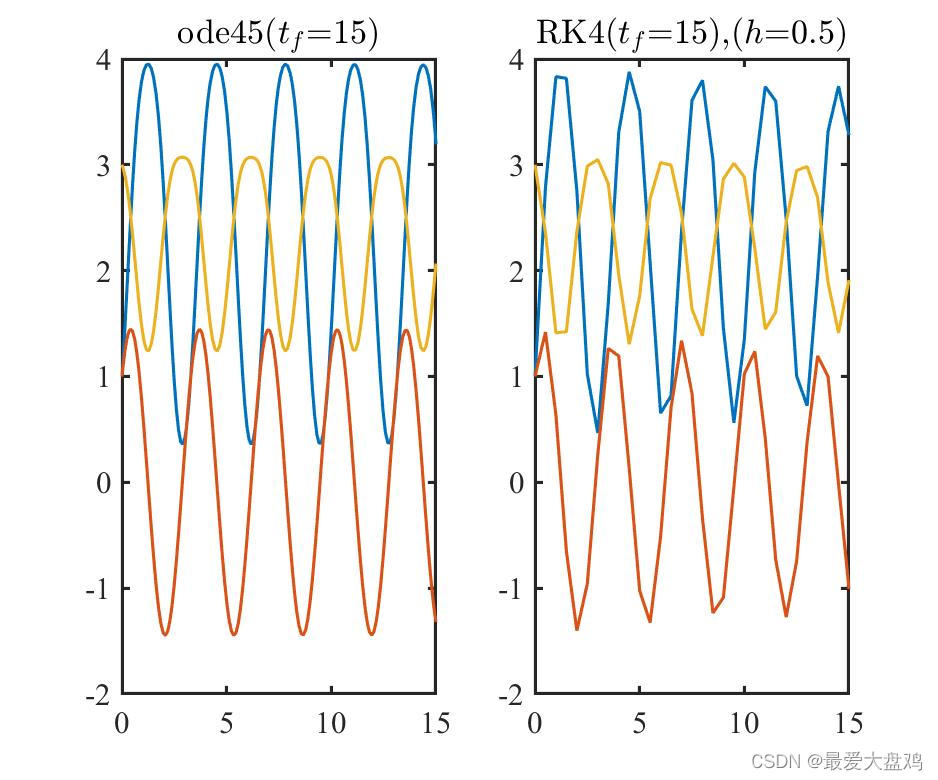
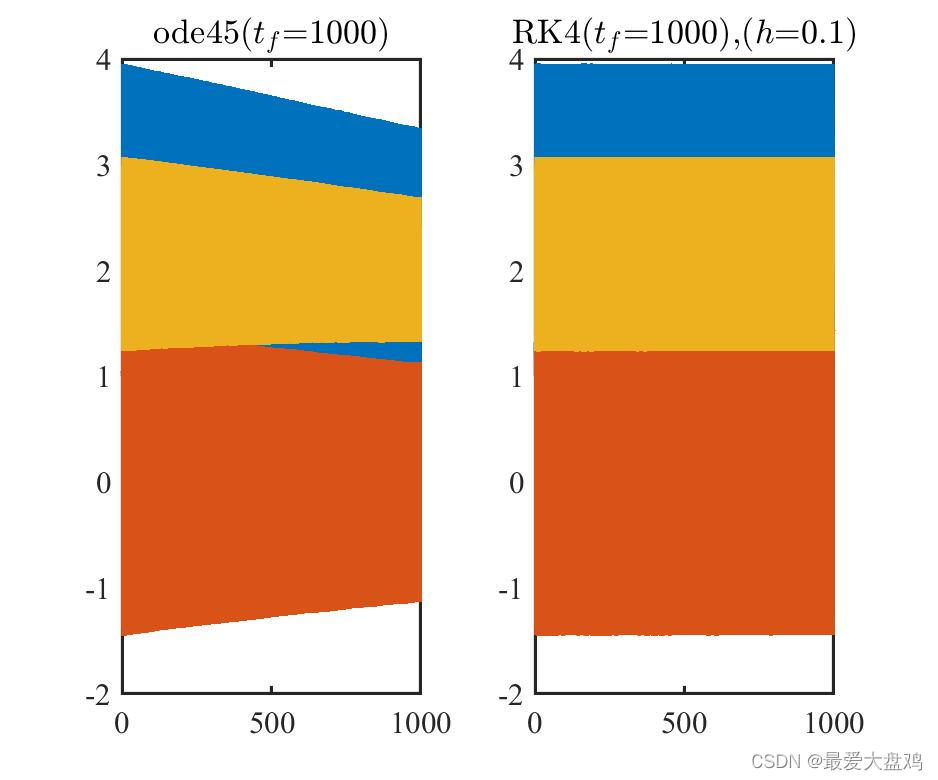
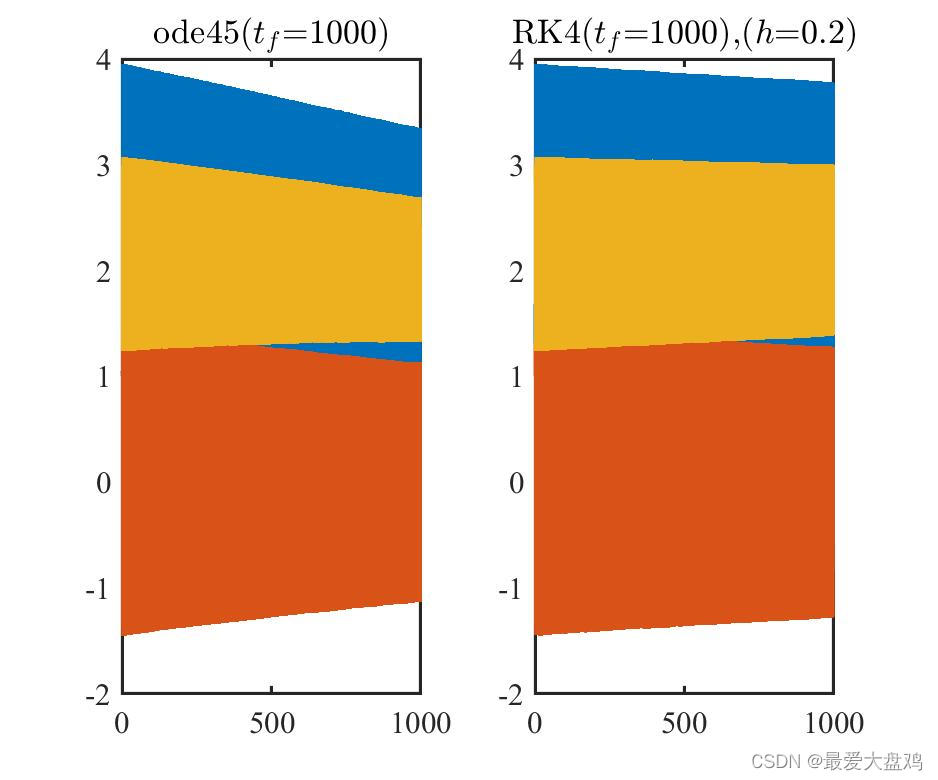
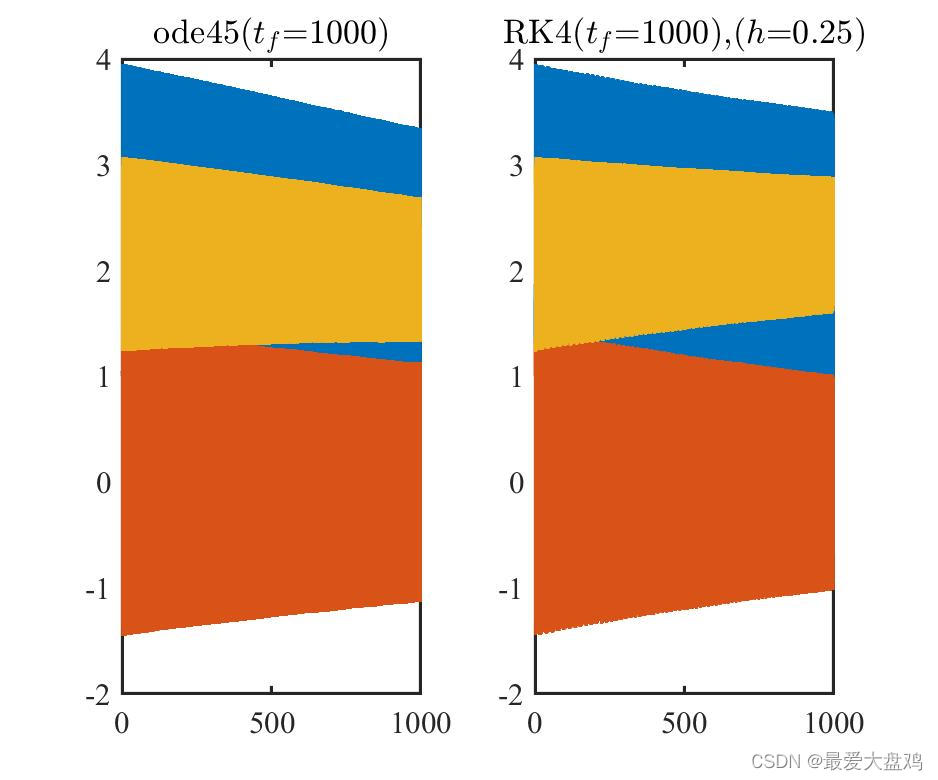
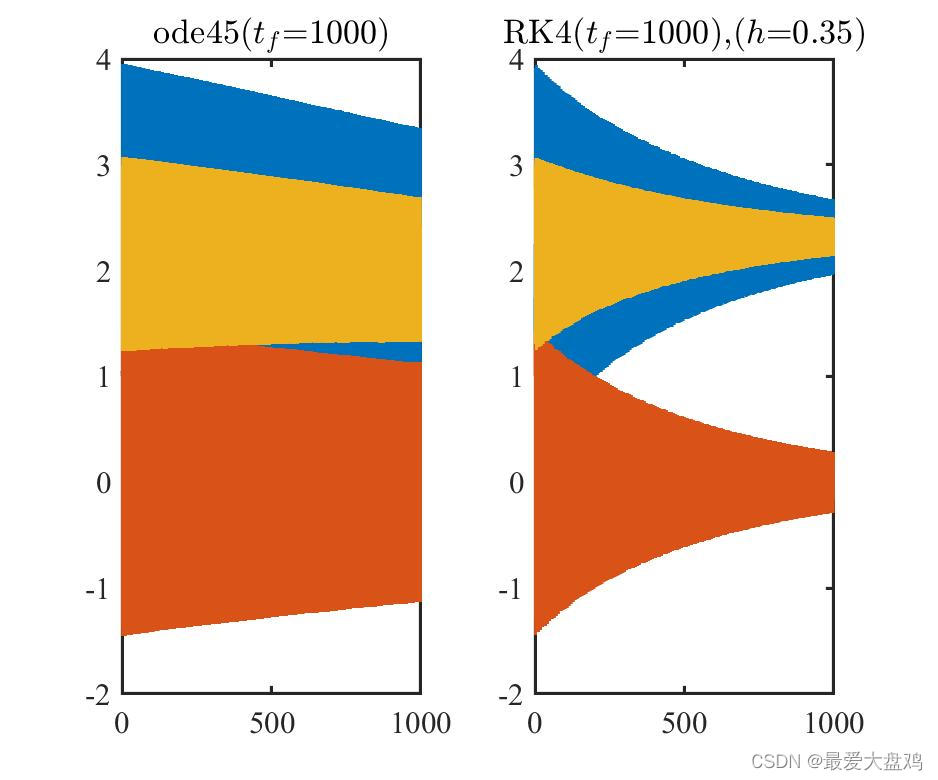
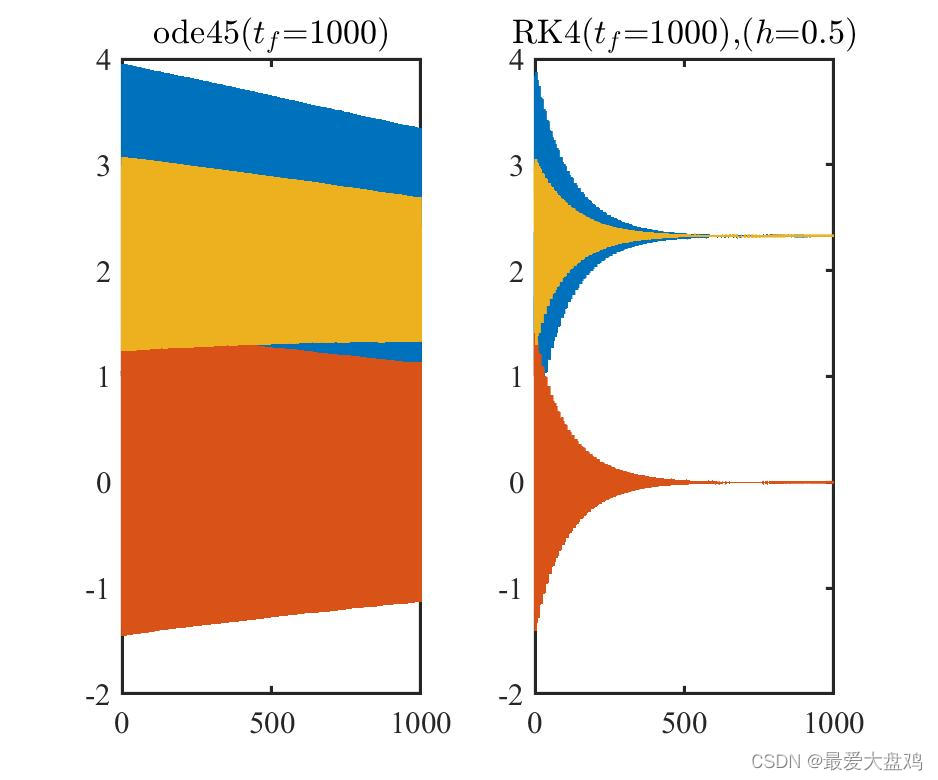
从计算精度来看，计算时间比较小的时候， RK 算法的步长越小，算的结果越和 ode45() 的结果接近，步长增加到 $h=0.35,0.5$ 的时候，得到的曲线已经呈现不光滑的趋势了。

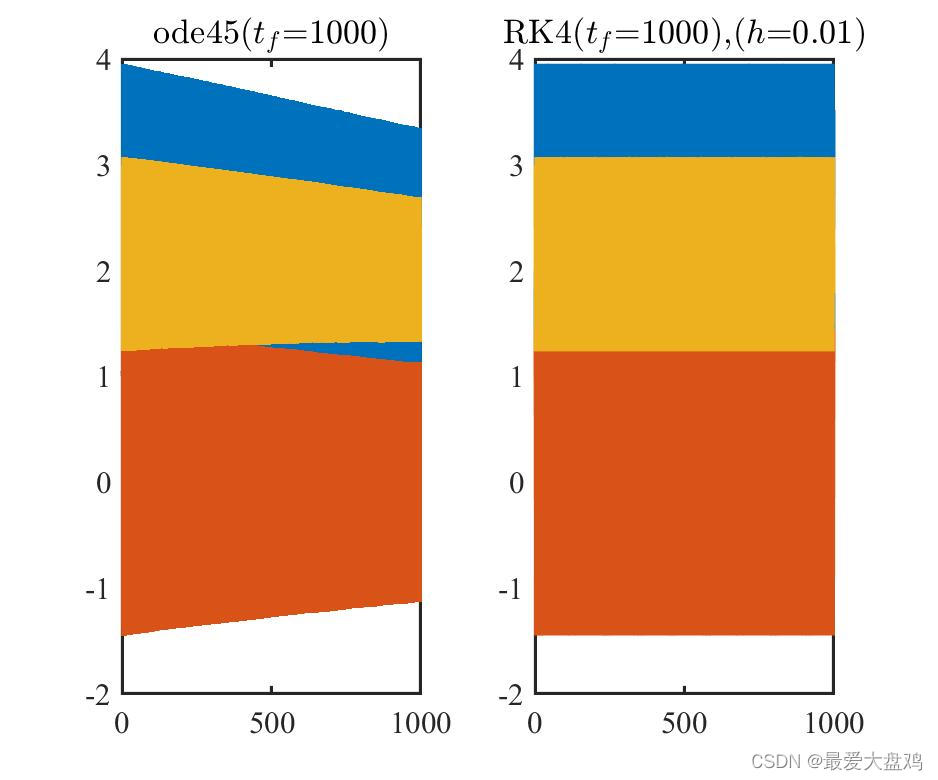
计算时间增大之后，，RK 算法精度跟不上 ode45() ，这个时候的步长选取就值得考虑了，可以发现，不论是步长取得过小（$h=0.01,0.10,0.20$），还是步长取得过大（$h=0.35,0.50$），得到的结果都和 ode45() 的结果不相符合，在 $h=0.25$ 时，Rk 算法求解微分方程的效果会好一些，和 ode45() 的结果有差距，但相较其他步长的结果来说，要更好一些。

从计算效率来看，RK 算法的步长越小，计算效率越低，因为步长小的话，每次更新迭代的值也小了，需要更多步才能迭代到理想值；步长大的时候，计算效率较高，但是计算精度较低。

结论

因此，可以得出结论，

• 在计算时间短的微分方程求解问题中，使用自编 RK 算法的计算精度与使用 ode45() 计算精度相近，计算效率更高；
• 在计算时间长的微分方程求解问题中，建议使用 ode45() 会得到更好的结果；
• RK 算法中，计算步长和计算时间区间是需要协调好的重要变量，把这 2 个变量设置好，计算精度和计算效率才会更加优越。

最后

以上就是娇气蚂蚁为你收集整理的MATLAB中ode45()和Runge-Kutta算法（4阶）的比较引言ode45()Runge-Kutta 算法RK 算法程序仿真结论的全部内容，希望文章能够帮你解决MATLAB中ode45()和Runge-Kutta算法（4阶）的比较引言ode45()Runge-Kutta 算法RK 算法程序仿真结论所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。