ode45求解微分方程

如何利用matlab中的ode45来求解一阶和二阶微分方程

建议大家先看ode45的使用文档，再来看我的博客，拿我这个当个练习做吧，文档链接在文章底部

1.求解一阶微分方程

这是随机共振中的Langevin方程，现在我们来求解x
先在matlab中新建一个脚本写一个函数
注：图中的D=0.31

function dx=funct(x,t)
dx=1*x-1*x^3+0.3*sin(2*pi*0.01*t)+sqrt(2*0.31)*randn(size(t));
end

在另一个脚本中调用这个函数

hh=ode45('funct',[0,1000],0);

这样就可以了，比一般的自己写一个利用龙格库塔四阶方法求解要简单的多，下边放一下这个方法

function x=sr(a,b,h,x1)
x=zeros(1,length(x1));
for i=1:length(x1)-1
k1=a*x(i)-b*x(i).^3+x1(i);
k2=a*(x(i)+k1*h/2)-b*(x(i)+k1*h/2).^3+x1(i);
k3=a*(x(i)+k2*h/2)-b*(x(i)+k2*h/2).^3+x1(i);
k4=a*(x(i)+k3*h)-b*(x(i)+h*k3).^3+x1(i);
x(i+1)=x(i)+(h/6)*(k1+2*k2+2*k3+k4);
end

这个里边还是有一点错误的（有几个参数写的不对，大家可以对照着数值分析的课本改一下）
好，下边来解一下二阶的微分方程

2.求解二阶微分方程

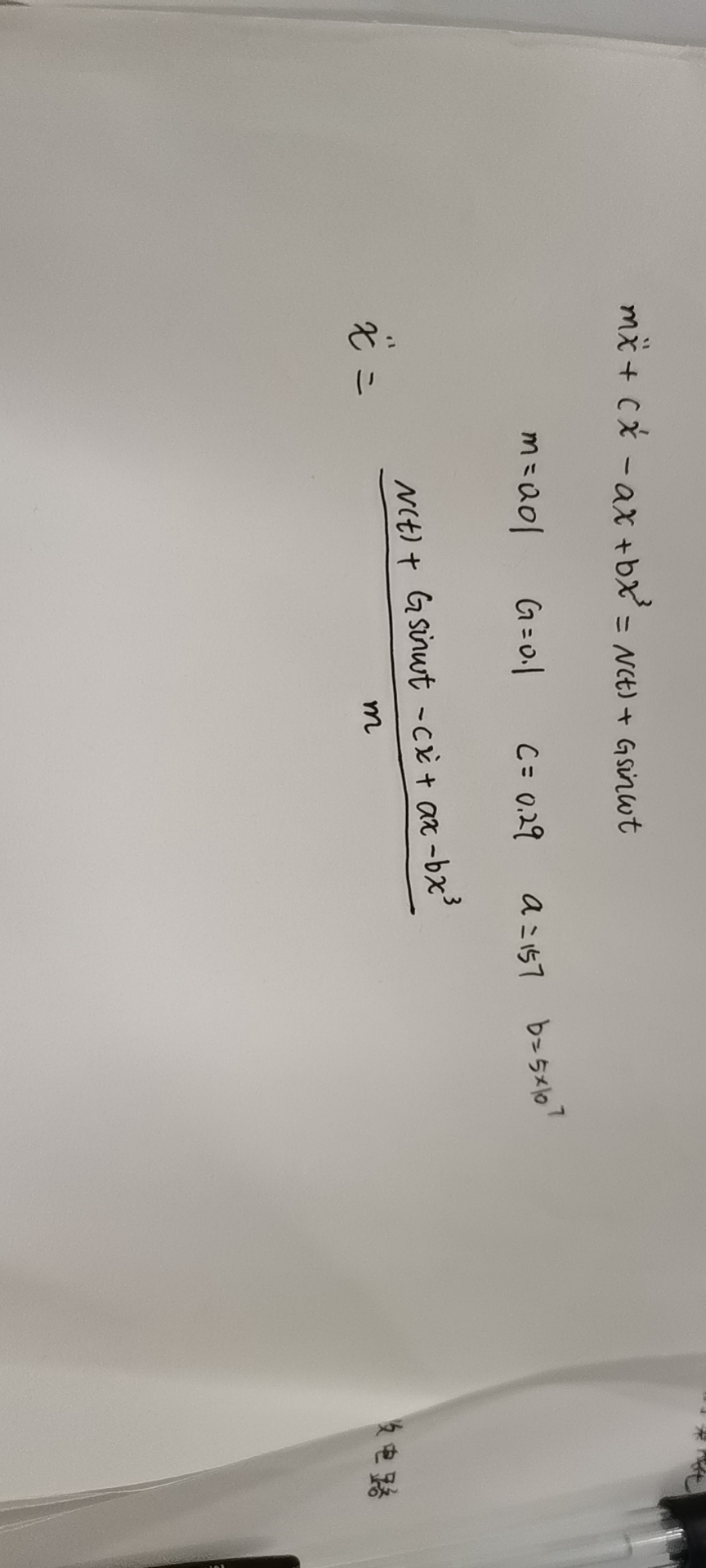
（这个图片不知道为啥正不过来0.0）
要先将二阶方程化成这种形式，然后就可以编写函数了

function xp=func(t,x)
xp=zeros(2,1);
xp(1)=x(2);
xp(2)=(157*x(1)-5*10^7*x(1).^3-0.29*x(2)+0.1*sin(50*t))/0.01;
end

[t,x]=ode45('func',[0,50],[0,0]);
plot(x(:,1),x(:,2));

（我这里t的取值本来是1000的，我给取小了一点，太大的话，程序要运行好久）
结果如下

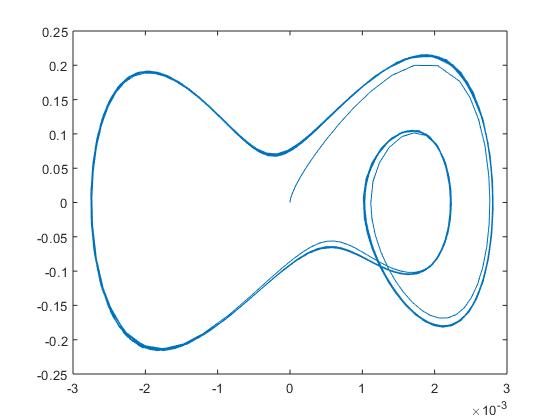
好了，以上就是利用matlab中的ode45来求解一阶或者二阶的微分方程了，妈妈再也不用担心我不会解方程了。。。。。。。
链接：https://pan.baidu.com/s/1BMxvd_J4Qorz1hYf3LDsyg
提取码：2333
复制这段内容后打开百度网盘手机App，操作更方便哦

最后

以上就是坚强牛排为你收集整理的ode45求解微分方程的全部内容，希望文章能够帮你解决ode45求解微分方程所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。