matlab梯形法求解微分方程和simulink对比

1、内容简介

略
590-可以交流、咨询、答疑

2、内容说明

略

3、仿真分析

close all
clear
clc
% 基本参数
M = 10;
K = 20;
B = 10;
ft = 50;
X1_0 = 0; % 初始值
X2_0 = 1; % 初始值
%%
tstep = 0.1; % 定义步长
t = 0:tstep:20; % 定义仿真时间
X1 = zeros(1,length(t));X1(1) = X1_0; % 定义变量X1和初始化
X2 = zeros(1,length(t));X2(1) = X2_0; % 定义变量X1和初始化
for n=2:length(t)
    X1(n) = X2(n-1)*tstep + X1(n-1); % 先求解X1
    X2(n) = (-K*X1(n)-B*X2(n-1)+ft)/M*tstep + X2(n-1); % 然后根据公式求解X2
end
figure
plot(t,X1)
title X1
grid on
figure
plot(t,X2)
title X2
grid on

% sim('model.mdl')
load('X1.mat')  % 加载simulink的仿真结果数据
load('X2.mat')  % 加载simulink的仿真结果数据
figure
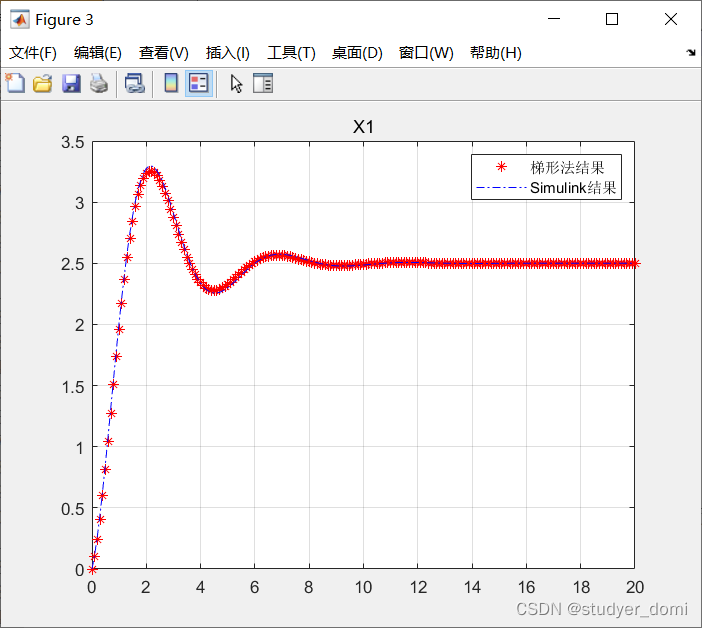
plot(t,X1,'r*',t,X1_s,'b-.')
title X1
grid on
legend('梯形法结果','Simulink结果')

figure
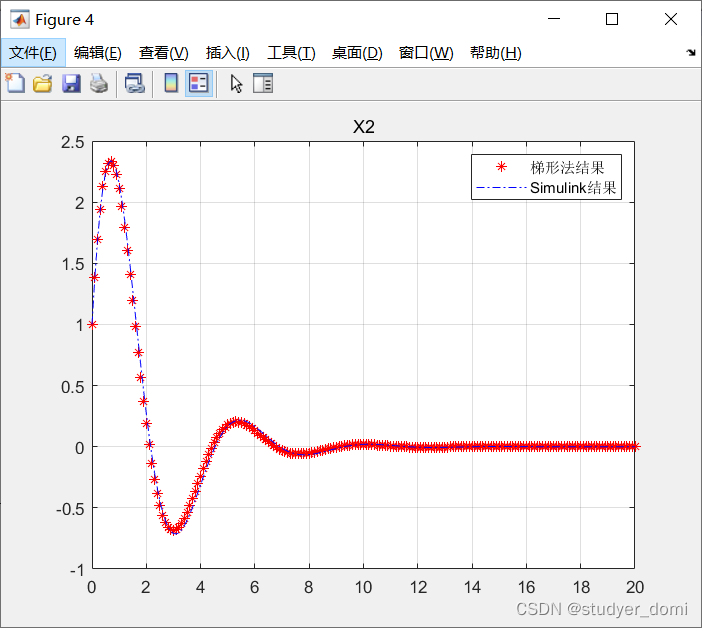
plot(t,X2,'r*',t,X2_s,'b-.')
title X2
grid on
legend('梯形法结果','Simulink结果')

4、参考论文

略

最后

以上就是文静曲奇最近收集整理的关于matlab梯形法求解微分方程和simulink对比的全部内容，更多相关matlab梯形法求解微分方程和simulink对比内容请搜索靠谱客的其他文章。