目录​​​​​​​

控制对象

连续对象离散化

设计数字观测器

考虑有限字长效应

设计加法器

缩放

仿真文件下载地址：数字观测器_考虑有限字长效益-智慧交通文档类资源-CSDN下载

控制对象

连续对象离散化

离散化的具体方法及证明参考现代控制论或计算机控制技术。这里只说明如何建模。

改写成连续状态空间方程形式

其中：

连续状态方程离散化

matlab代码如下：

1
2
Ad=expm(AH*Tk)
Bd = Ad*inv(AH)*([1 0;0 1]-inv(Ad))*BH

simulink仿真图图下：

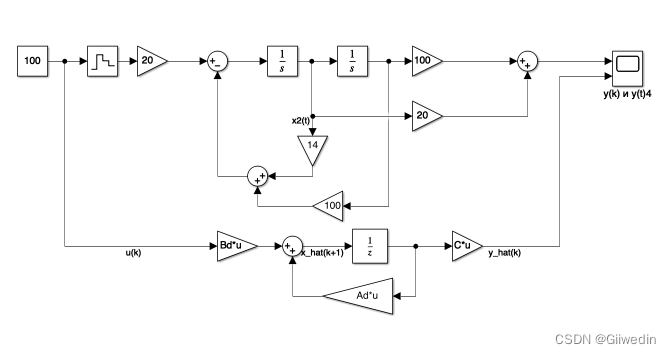
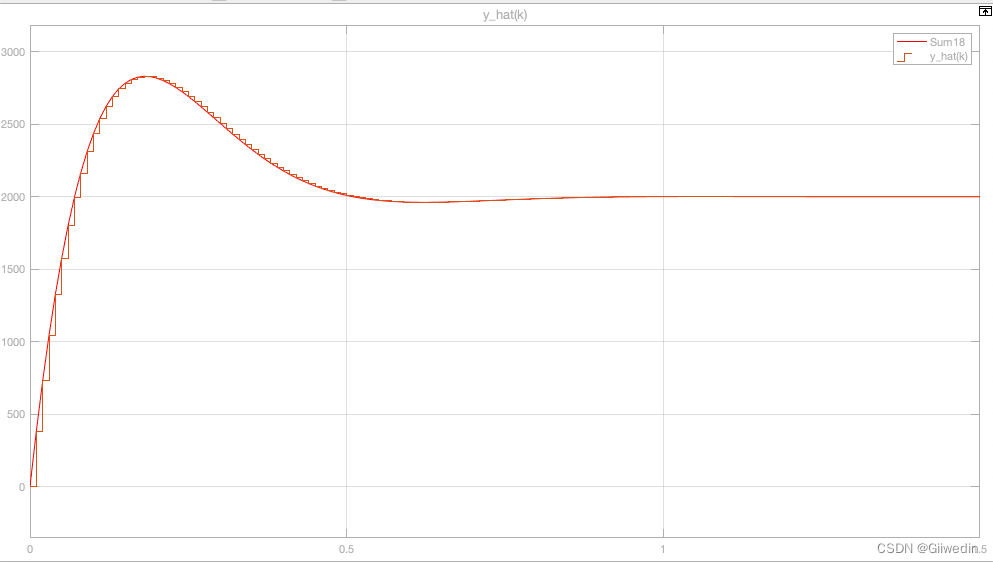
离散化系统与原系统输出比较

​​​​​​​

设计数字观测器

全维数字状态观测器设计的计算可参考计算机控制技术

判断系统可观性：

1
2
3
>> rank(obsv(AH,C))
ans =
2

系统可观 

离散系统全维状态观测器方程

其中

计算反馈矩阵G

假设希望观测器的特征根位于 其中原状态方程特征根的最小值。使用maltab命令acker计算G

1
2
3
4
5
6
lamdaA = eig(Ad);
lamda = abs(max(eig(Ad)))^5+(abs(min(eig(Ad)))^3-abs(min(eig(Ad)))^5)*rand();
Lamda = [lamda;lamda];
%------------------------------------------------------------------------------%
G = acker(Ad',C',Lamda);
K = G'; 

带观测器的simulink模型 

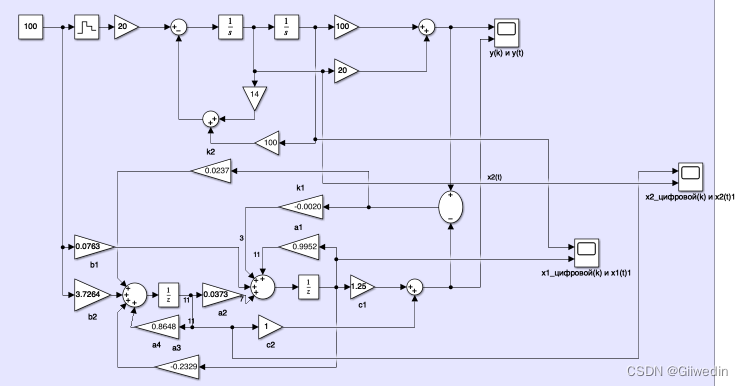
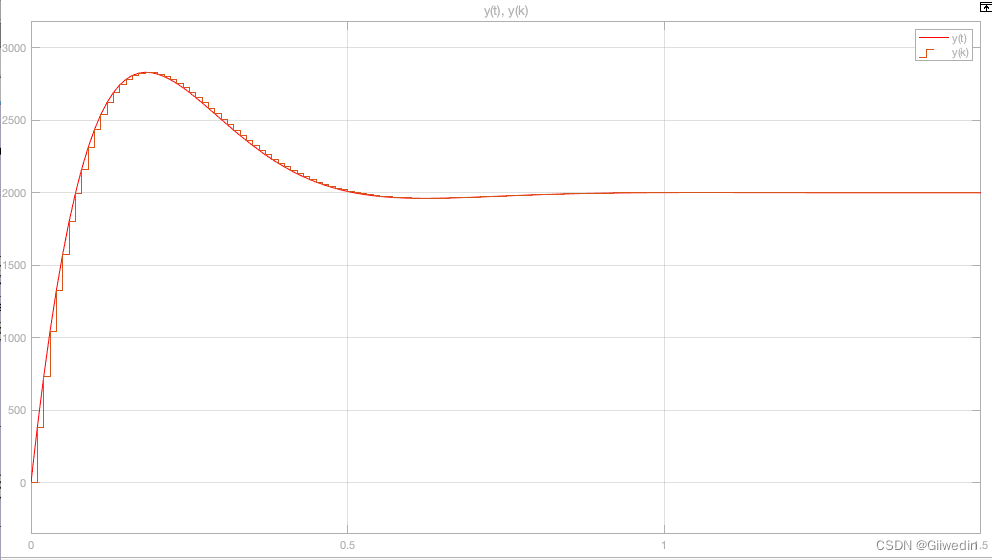
考虑有限字长效应

设计加法器

数字观测器在物理实现时，计算硬件的位数是不无限的，因此设计观测器前需要考虑有限字长效应。在这个例子中考虑加法器的有限字长效应。上一小节中输出y最大值2831<2^12因此加法器的最大位数为12。

设计加法器，使用simulink中的S-Function Builder 模块

打开模块进行设置 ，加法器有两个输入一个输出一个参数如下图

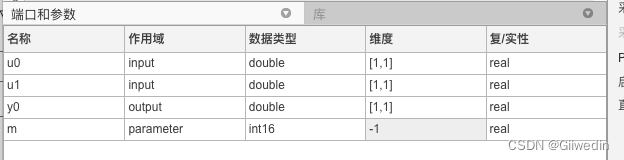
 在/* Output_BEGIN */下方输入如下代码后编译

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
%%%参数m 加法器的位数
long x1,x2,M,n1;
int n;
n=m[0];
M=1;
while (n>0)
{M=M*2;
n--;}
M=M-1;
n1=u0[0];
if(n1>=0) x1=n1&M;
else x1= -((-n1)&M);
n1=u1[0];
if(n1>=0) x2=n1&M;
else x2= -((-n1)&M);
y0[0]=x1+x2;

然后将原模型中的加法器替换如下图

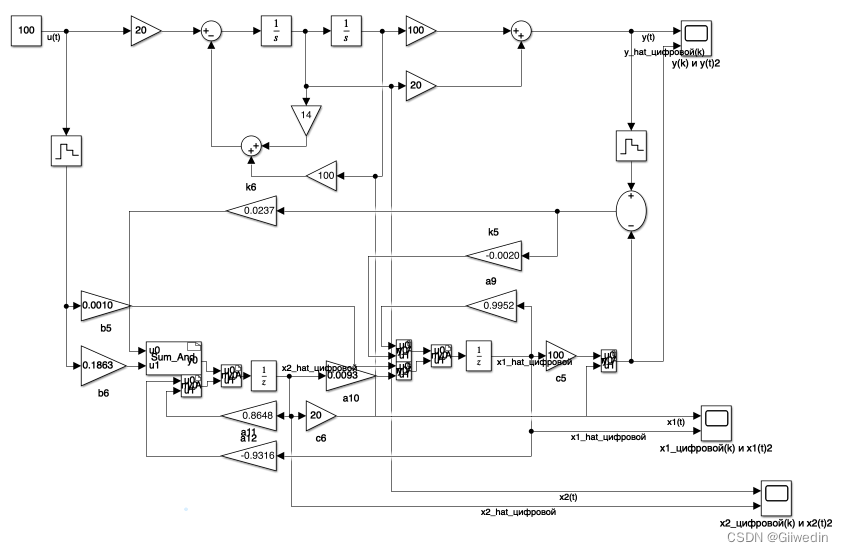
 进行仿真

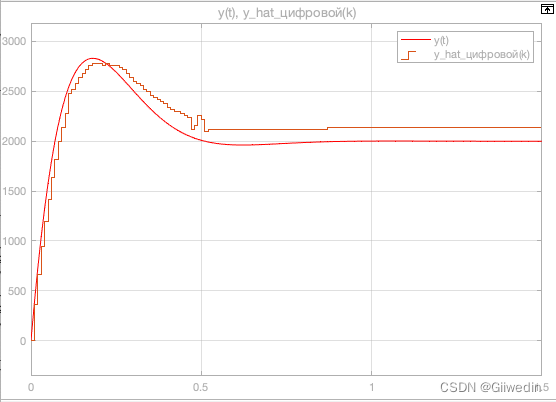
 可以看到观测器的输入与控制对象的输出在稳态时有误差，注意到图中的增益模块gain的系数很小使得进入到加法器的值很小，而加法器只能表示整数，因此导致较大的误差，为了解决这个问题，使用缩放方法减小稳态误差。

缩放

例如将状态分别缩小百分之80和20，则可以得到新的状态方程，其中ds

matlab 代码

1
2
3
4
5
6
7
m1=1/80;
m2=1/20;
M=[m1 0;0 m2];
AD = inv(M)*Ad*M
BD = inv(M)*Bd
CD = C*M

simulink仿真图

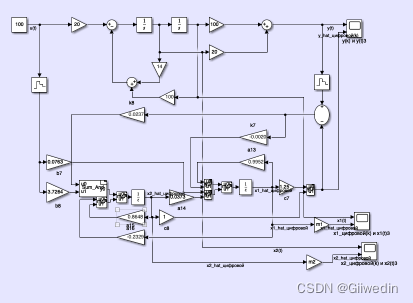
注意到此时增益数比原模型的要大一些，因此推断数字系统观测器的输出与原系统输出的稳态误差应该会减少。

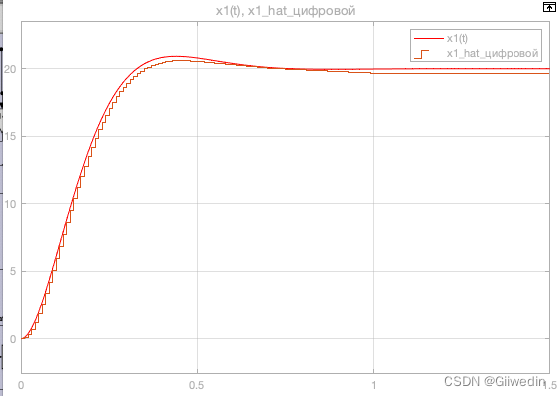
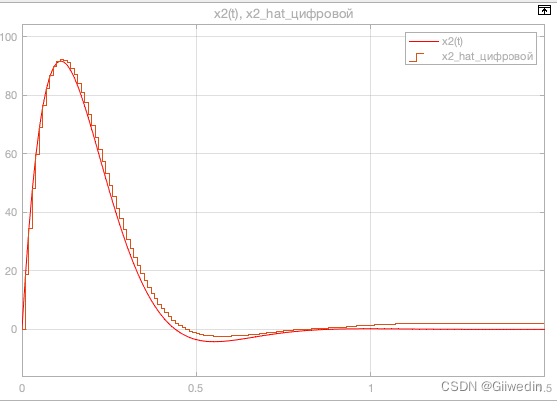
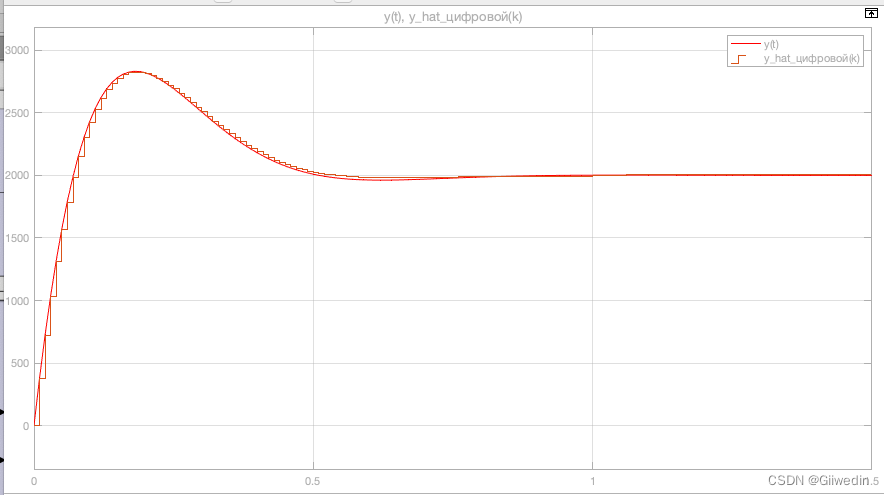
观测器与控制对象状态变量和输出的比较

上图证明了推断，对系统状态变量的缩放的确可以降低有限字长效应的影响，并且注意到数字观测器和原系统的状态变量仍然存在稳态误差，因此缩放只是降低了误差而不是消除。

仿真文件下载地址：数字观测器_考虑有限字长效益-智慧交通文档类资源-CSDN下载

相关文章：

使用simulink仿真连续(离散)线性定长系统全维渐进状态观测器_Giiwedin的博客-CSDN博客

使用drem对控制系统进行参数估计simulink仿真_Giiwedin的博客-CSDN博客

对给定干扰信号的simulink数字控制系统仿真_Giiwedin的博客-CSDN博客_simulink扰动信号

二相混合式步进电机闭环矢量控制simulink仿真（含仿真文件）_Giiwedin的博客-CSDN博客_步进电机数学模型

二相混合式步进电机开环细分控制simulink建模仿真含模型文件_Giiwedin的博客-CSDN博客

二相混合式步进电机simulink仿真简单的驱动器建模（含模型文件）_Giiwedin的博客-CSDN博客_步进电机simulink模型

最后

以上就是鲜艳电话最近收集整理的关于考虑有限字长效应的全维数字观测器simulink仿真及应对方法控制对象连续对象离散化设计数字观测器考虑有限字长效应仿真文件下载地址：数字观测器_考虑有限字长效益-智慧交通文档类资源-CSDN下载的全部内容，更多相关考虑有限字长效应内容请搜索靠谱客的其他文章。