目录
系统模型:
闭环极点设计分离性
设计系统输出反馈系数K
转换标准能控型
设计反馈矩阵G
仿真
matlab代码
simulink模型
仿真结果
仿真程序下载地址:连续定常系统全维状态观测器simulink仿真m代码-智慧城市文档类资源-CSDN下载
全维数字观测器输出反馈-智能家居文档类资源-CSDN下载
系统模型:
闭环极点设计分离性
闭环系统的极点包括直接状态反馈系统
的极点和观测器
的极点两部分。但二者独立,相互分离。表明,由观测器构成状态反馈的闭环系统,其特征多项式等于矩阵(A+BK)与矩阵(A-GC)的特征多项式的乘积。亦即闭环系统的极点等于直接状态反馈(A+BK)的极点和状态观测器(A-GC)的极点之总和,而且二者相互独立。因此只要系统(A,B,C)能控能观,则系统的状态反馈矩阵K和观测器反馈矩阵G可分别进行设计。这个性质称为闭环极点设计的分离性。
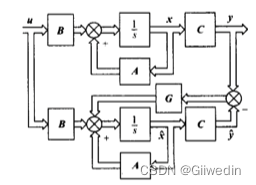
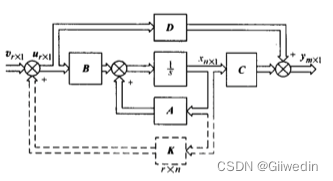
图1 渐进状态观测器 图2输出反馈
设计系统输出反馈系数K
证明系统能控性
转换标准能控型
系统传递函数
线性非奇异变换矩阵
标准能控1型
加入状态反馈增益矩阵
闭环特征多项式
使闭环极点与期望的极点相符求出增益K
设计反馈矩阵G
验证系统能观
观测器方程
非奇异变换
能观标准2型
闭环特征多项式
使闭环极点与期望的极点相符求出增益G
仿真
matlab代码
clear
A = [0 -1 0 0;0 0 2 3;0 0 0 -1;0 0 0 0];
B = [0;0;0;1];
C = [1 0 0 0];
%配置目标极点
K = acker(A,B,[-1,-1,-1+i,-1-i]);
%设计观测器
G=acker(A',C',[-1,-1,-1,-1])';
simulink模型
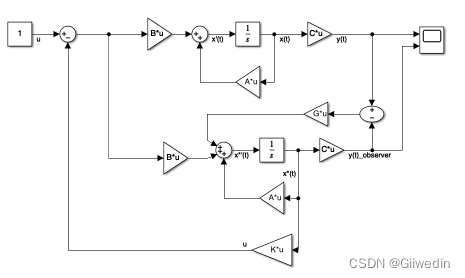
仿真结果
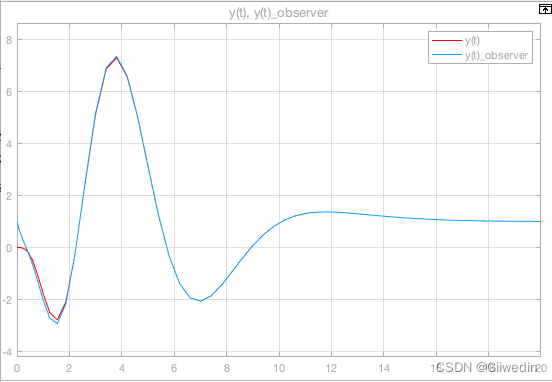
仿真程序下载地址:连续定常系统全维状态观测器simulink仿真m代码-智慧城市文档类资源-CSDN下载
全维数字观测器输出反馈-智能家居文档类资源-CSDN下载
相关文章:
使用simulink仿真连续(离散)线性定长系统全维渐进状态观测器_Giiwedin的博客-CSDN博客
使用drem对控制系统进行参数估计simulink仿真_Giiwedin的博客-CSDN博客
对给定干扰信号的simulink数字控制系统仿真_Giiwedin的博客-CSDN博客_simulink扰动信号
二相混合式步进电机闭环矢量控制simulink仿真(含仿真文件)_Giiwedin的博客-CSDN博客_步进电机数学模型
二相混合式步进电机开环细分控制simulink建模仿真含模型文件_Giiwedin的博客-CSDN博客
最后
以上就是从容大地最近收集整理的关于使用simulink仿真连续(离散)线性定长系统全维渐进状态观测器系统模型:闭环极点设计分离性设计系统输出反馈系数K设计反馈矩阵G仿真 仿真程序下载地址:连续定常系统全维状态观测器simulink仿真m代码-智慧城市文档类资源-CSDN下载全维数字观测器输出反馈-智能家居文档类资源-CSDN下载的全部内容,更多相关使用simulink仿真连续(离散)线性定长系统全维渐进状态观测器系统模型内容请搜索靠谱客的其他文章。








发表评论 取消回复