【ADRC】扩张状态观测器(ESO)

扩张状态观测器是自抗扰控制中非常重要的一个环节，在我学习这部分内容后，在写本篇文章时，大致可以按照三个步骤来做实验，推导，由这三个步骤来由浅入深地去理解扩张状态观测器(ESO)，即：线性状态观测器，非线性状态观测器，扩张状态观测器。前面这两个名称是我为了区分自己起的，不一定是专业术语，不过可以跟着步骤一起来看一下。

线性状态观测器

这类状态观测器可以称之为最基本的状态观测器，推导过程可以不用赘述，可以查看我之前的相关文章。大致的含义就是我们知道系统的模型是怎样的，系统状态的各个参数我们都可以获取，这种情况下，我们可以直接使用系统参数来复制一个系统，从而观测系统的状态。我们可以直接使用一个例子来做一下实验。

假设有以下这个系统，我们可以写出观测器的标准形式：

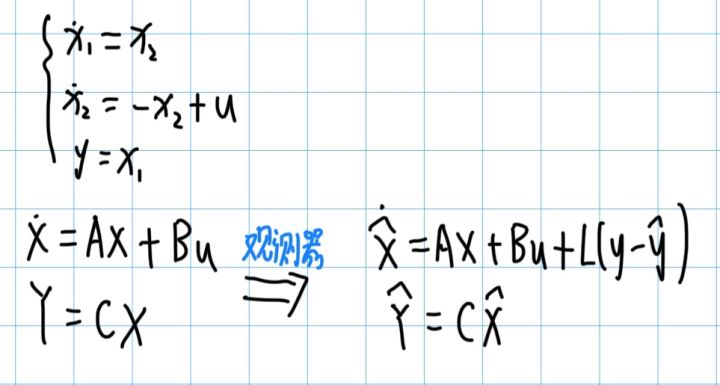
在自抗扰的资料与书籍中都是用状态 Z 来代替观测器的估计值 X_hat ，为了方便后续对照，我们在这里也都写作 Z 好了，自己清楚 Z 就是估计状态 X_hat 即可，其实是与标准的现代控制书中是一样的：

这里我们可以定义一个变量 e = y_hat - y ，输出状态y的估计值减去实际输出y，即控制e收敛之后，便可以得到正确的观测状态，之后观测器的表达式就可以写作：

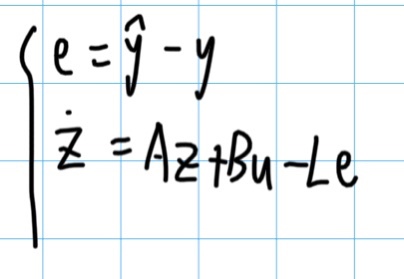
之后我们选择合适的L矩阵的参数，就可以使得状态收敛。回归我们给出的例子系统，我们可以列出观测器的微分方程：

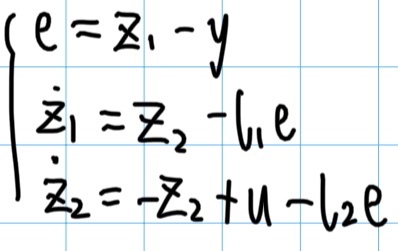
之后我们可以搭建一下这个模型试试看：

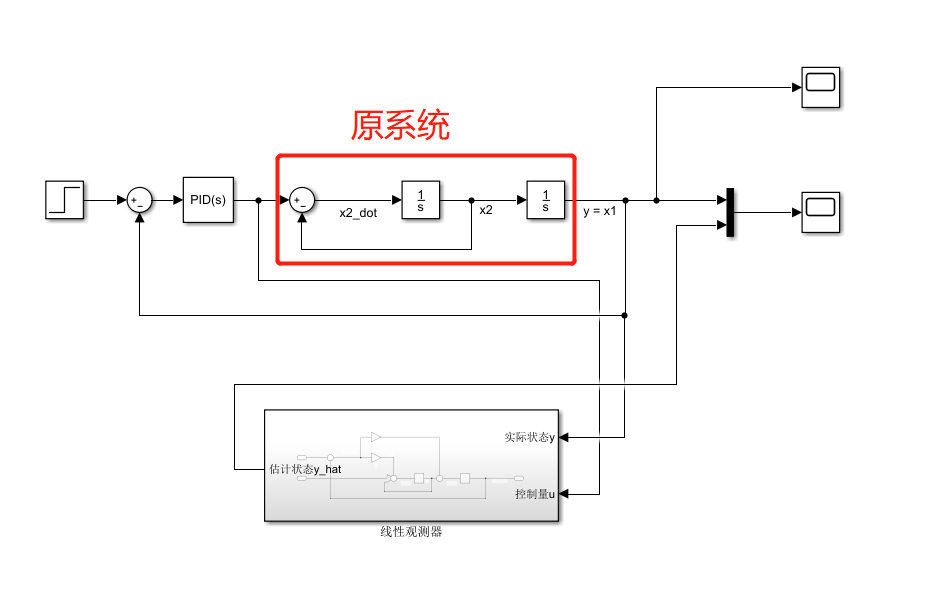
这里的PID模块只是我给的一个输入控制量u，它并不能使系统稳定，我随便给的参数，本章的关键是观测器是否收敛跟随，因此它不稳定也不影响测试，我们可以看到此时系统的输出：

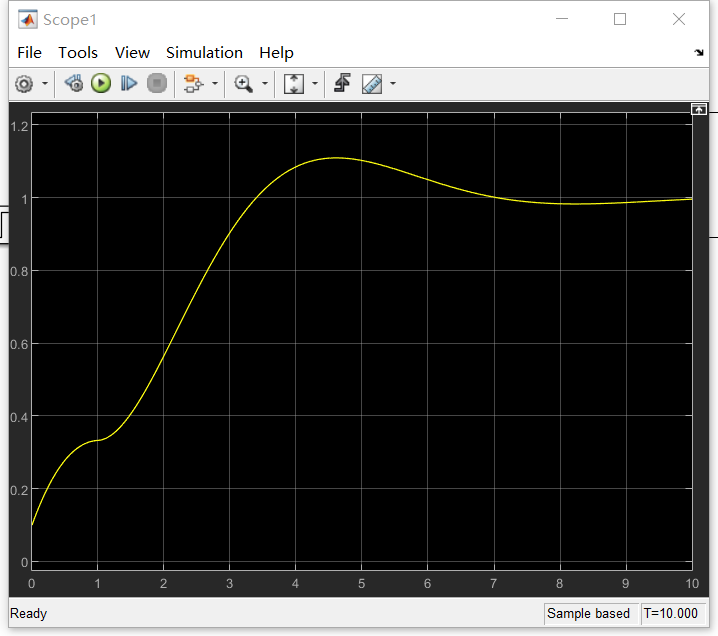
之后按照上述的观测器方程建立观测器模型：

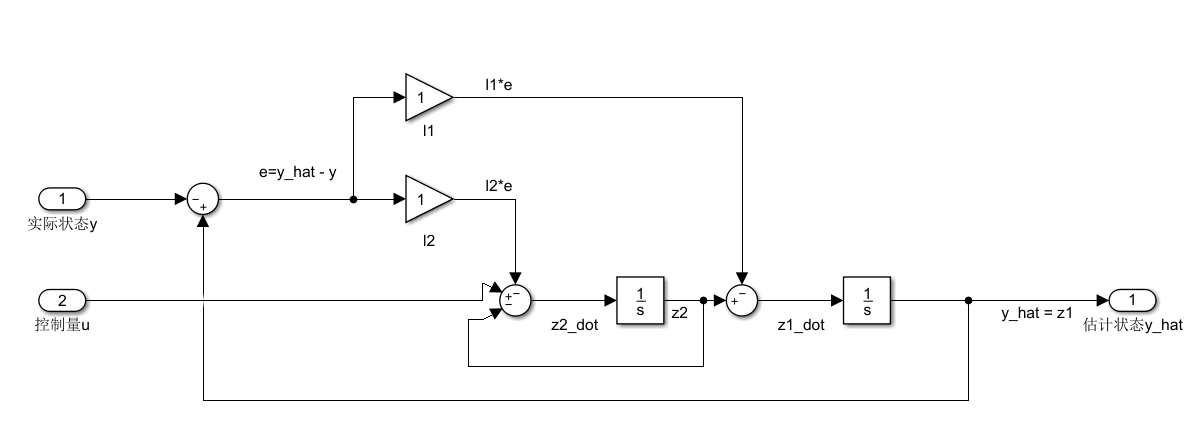
之后我们可以给x1，x2都一个初始值，不为0，这样就可以看到观测器的收敛过程：

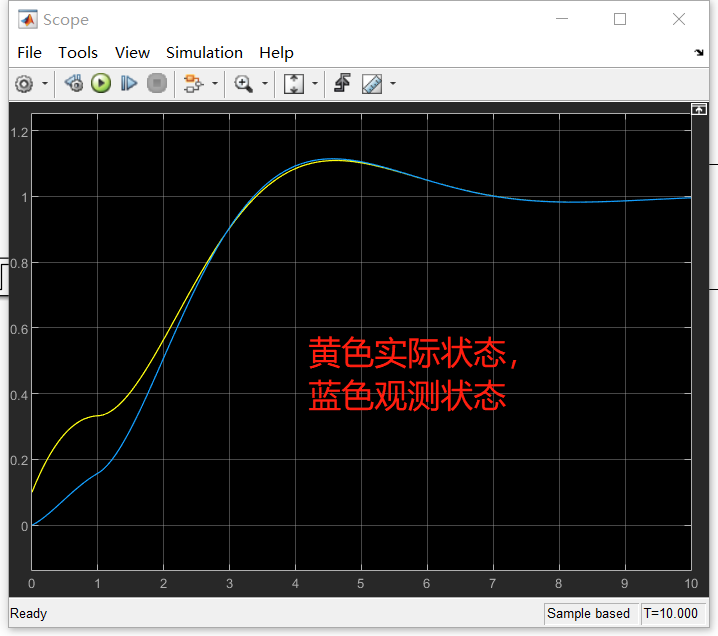
可以看到最终观测器的输出收敛到实际输出，这样便是一个基本的线性观测器。这种观测器是建立在我们已知系统参数的情况下，即A矩阵，B矩阵已知，那如果我们不知道系统参数的情况下，需要如何建立观测器？这便引出非线性观测器的概念。

非线性观测器

假如我们不知道系统参数，那么我们可以所幸建立观测器的时候就不加入系统参数，直接将其忽略，之后使用非线性函数g，使其收敛：

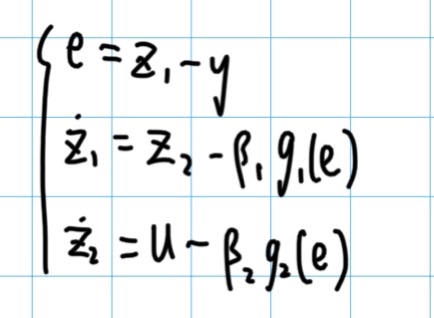
只要调试系数 β，以及选取合适的非线性函数g，就可以使其收敛，这里的 g 的一般形式选取为：

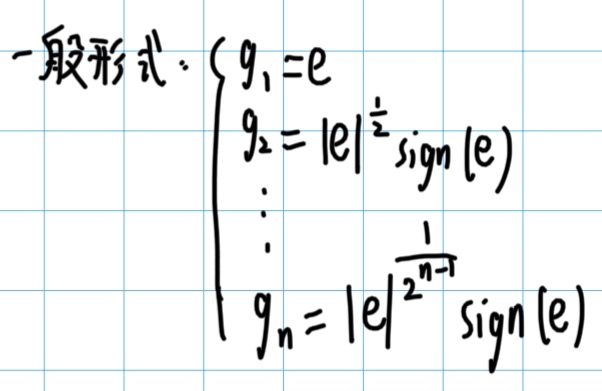
换算到例子中的系统为：

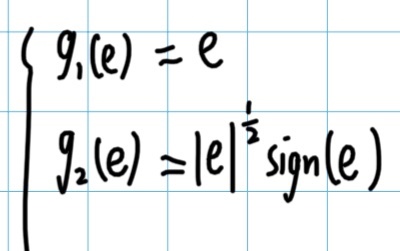
我们可以建立出这个非线性观测器的模型，看看收敛效果：

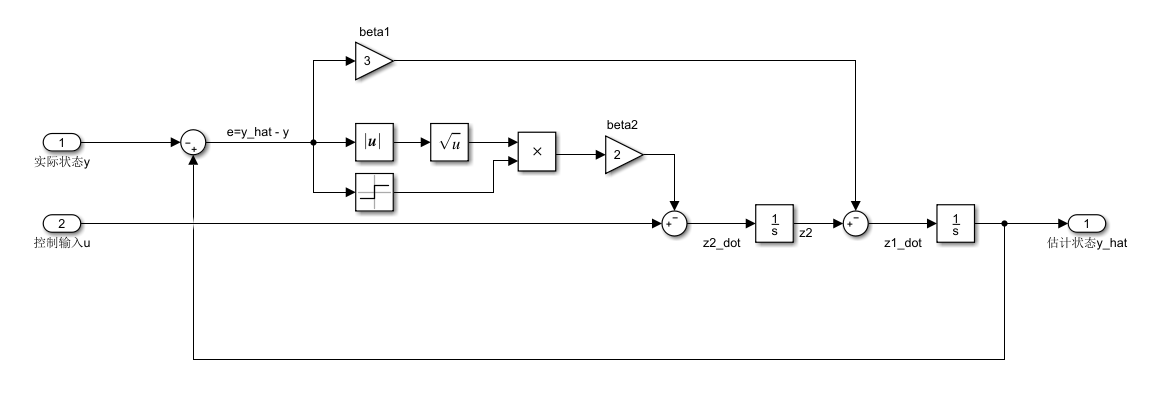
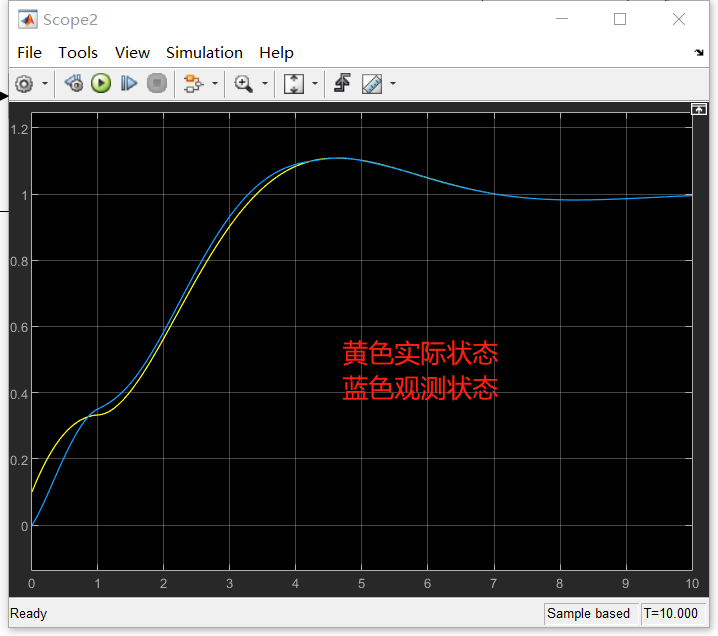
这里我们是没有将系统参数传入观测器的，但实际的观测器输出还是可以收敛，不过我们是假设了跟原系统一样的阶数，原系统为双积分系统，观测器我们也是假设了双积分系统，如果我们将观测器改成三积分的话，多一阶，可以看看实际效果：

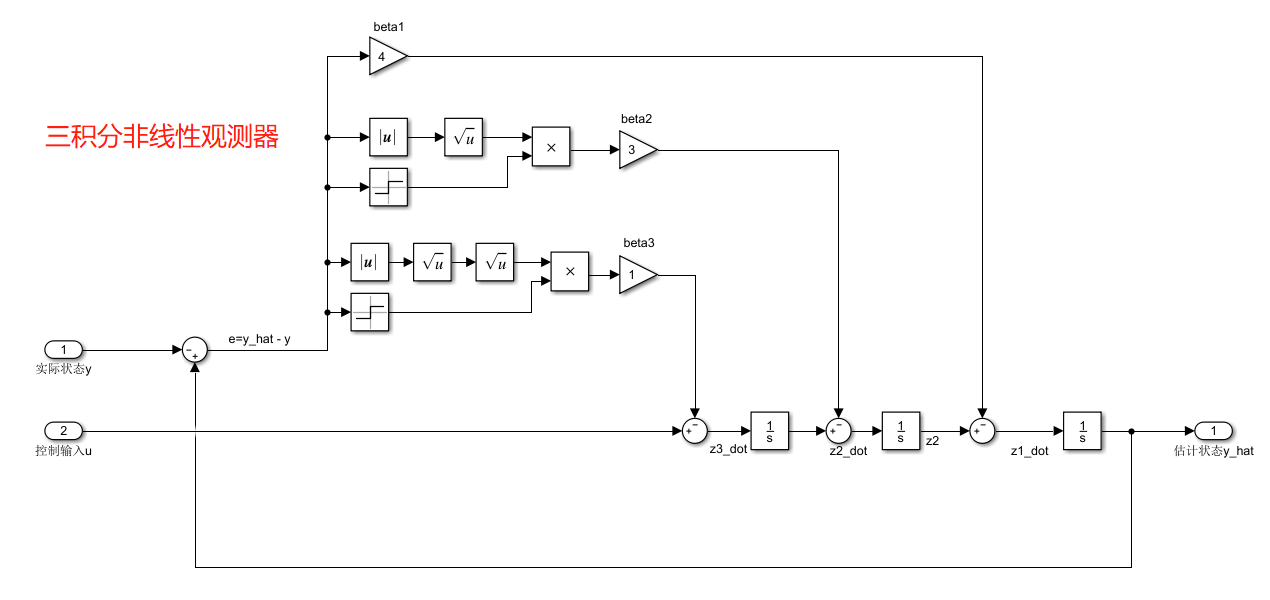
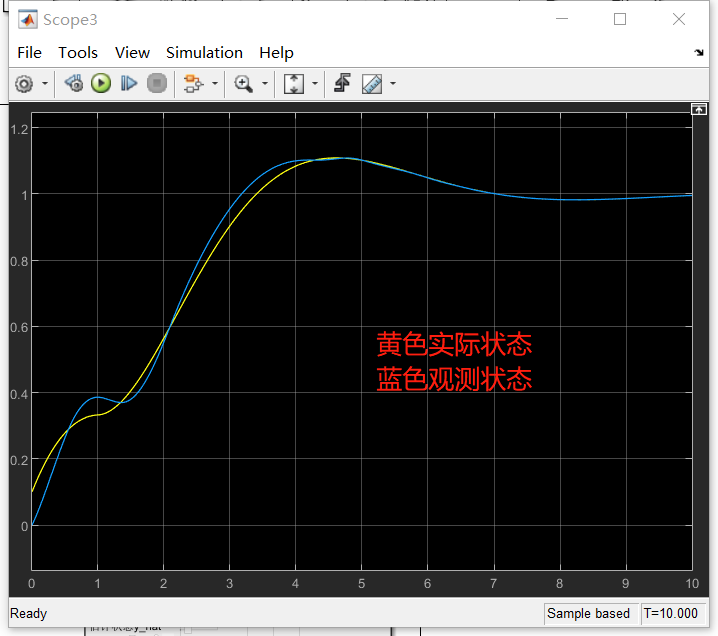
看起来也是没问题的。

扩张状态观测器

如果说上述不知道原系统参数的非线性观测器对于目标状态有很好的跟踪效果的话，那么我们之后就可以将系统的扰动加上，将扰动记作 w，之后可以将最后一个状态的微分方程中，除控制量u的其他作用量都记作 f(x1,x2,t,w) ，即 f 是x1，x2，t，还有扰动w的非线性函数，如下：

在此基础上，增加一个状态量 x3_dot = f(x1,x2,t,w)，在观测器中记作 z3，用来观测这个非线性函数 f ，这样增加一个状态量的观测器，就是扩张状态观测器：

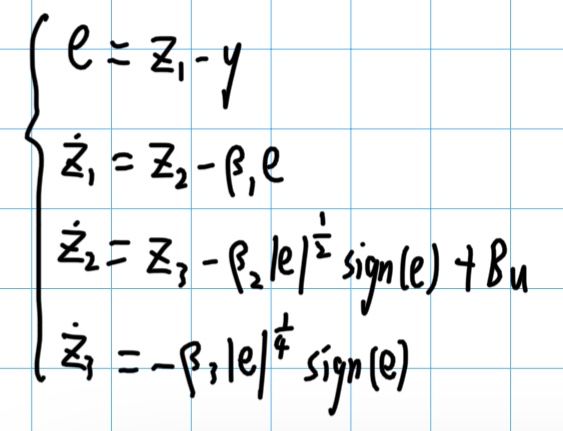
以上我们都默认控制量的增益为1，即 b = 1，建立模型后，将扰动也引出来：

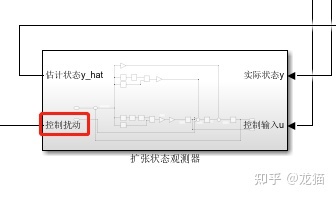
另外我们可以将原系统的控制量上增加一个扰动，让实际的控制量与控制器输出的控制量有偏差：

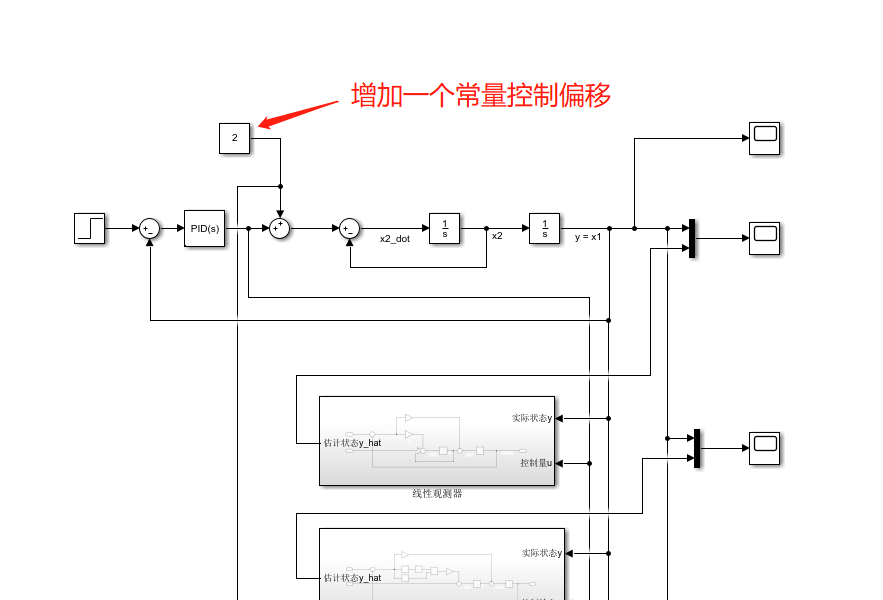
之后可以看到实际的状态跟随效果：

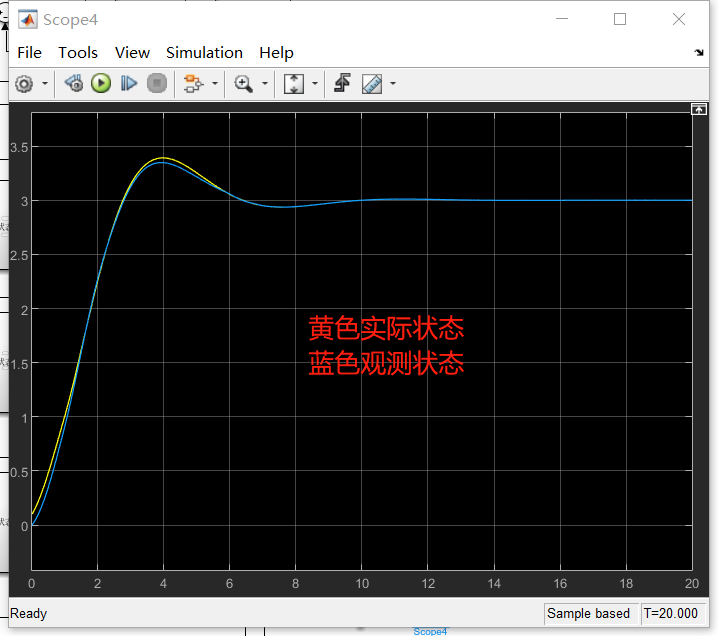
而且我们也可以看到对于扰动的观测效果：

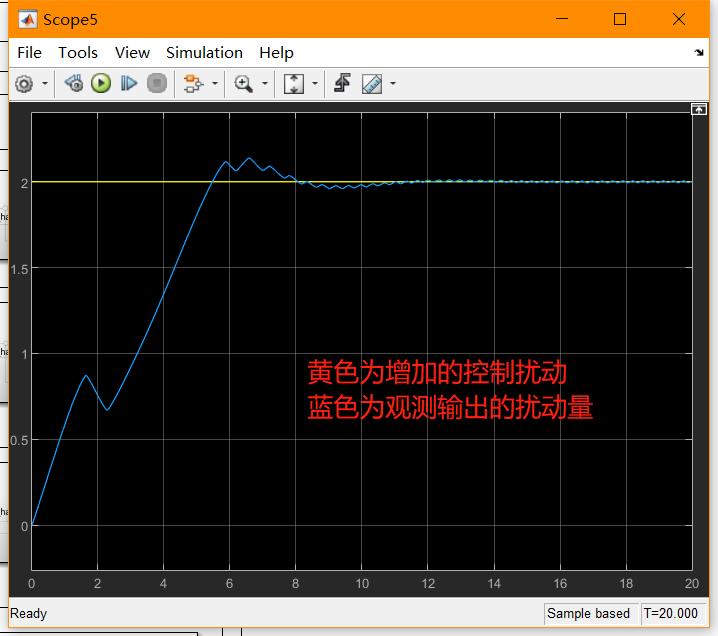
最后

以上就是典雅灯泡为你收集整理的【ADRC】扩张状态观测器(ESO)的全部内容，希望文章能够帮你解决【ADRC】扩张状态观测器(ESO)所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。