今天看扩张观测器，根据文献[1]的模型和控制算法，自己写了一份仿真代码。

% 2021.7.16 基于广义扩张状态观测器的干扰不匹配离散系统状态反馈控制
clc; clear all; close all;
set(0,'defaultfigurecolor','w');
%% 建模
% 连续模型(1)
nx=2; % x的维度
Ac=[0 1; -0.0011 -40;];
buc=[0 39005.6]';
bdc=[0 -55248.6]';
% 离散化(2)
T0=0.001;
[Phi, Gamma_u]=c2d(Ac,buc,T0);
[~, Gamma_d]=c2d(Ac,bdc,T0);
C=[1 0];
% 增广(4)
Theta=[Phi, Gamma_d; zeros(1, nx) 1];
Delta_u=[Gamma_u; 0];
Delta_h=[zeros(2,1); 1];
H=[C, 0];
%% 观测器
% Qo=obsv(Theta, H);
% rank(Qo) % 3
po=[0.1 0.1 0.1];
L=acker(Theta', H',po)';
%% 控制器
% Qcx=ctrb(Theta(1:2,1:2), Delta_u(1:2));
% rank(Qcx) % 2
pcx=[0.2 0.3];
Kx=-acker(Theta(1:2,1:2), Delta_u(1:2),pcx);
Kd=-Gamma_u'*Gamma_d/(norm(Gamma_u,2)^2);
%% 仿真
span=0.2;
N=floor(span/T0)+1;
x=zeros(nx,N); x(:,1)=randn(2,1);
x_hat=zeros(nx,N);
d=zeros(1,N);
d_hat=zeros(1,N);
u=zeros(1,N);
y=zeros(1,N); y(1)=C*x(:,1);
h=0.1*T0^3*ones(1,N);
xi_hat=zeros(nx+1,N);
for k=1:N-1
% 真实系统
x(:,k+1)=Phi*x(:,k)+Gamma_u*u(k)+Gamma_d*d(k);
d(k+1)=d(k)+h(k);
if k==floor(N/2)
d(k+1)=d(k+1)+0.1;
end
y(:,k+1)=C*x(:,k+1);
% 估计器
xi_hat(:,k+1)=Theta*xi_hat(:,k)+Delta_u*u(k)+Delta_h*h(k)+L*(y(k)-H*xi_hat(:,k));
x_hat(:,k+1)=xi_hat(1:nx,k+1);
d_hat(k+1)=xi_hat(end,k+1);
u(k+1)=Kx*x_hat(:,k+1)+Kd*d_hat(:,k+1);
end
ex=x-x_hat;
ed=d-d_hat;
%% 画图
figure(); hold on; grid on;
subplot(3,1,1); plot(0:T0:span, x(1,:), 'LineWidth',1);
xlabel('time/s'),ylabel('x_1');
subplot(3,1,2); plot(0:T0:span, x(2,:), 'LineWidth',1);
xlabel('time/s'),ylabel('x_2');
subplot(3,1,3); plot(0:T0:span, d, 'LineWidth',1);
xlabel('time/s'),ylabel('d');
suptitle('状态与干扰变化');
figure(); hold on; grid on;
subplot(3,1,1); plot(0:T0:span, ex(1,:), 'LineWidth',1);
xlabel('time/s'),ylabel('e_{x1}');
subplot(3,1,2); plot(0:T0:span, ex(2,:), 'LineWidth',1);
xlabel('time/s'),ylabel('e_{x2}');
subplot(3,1,3); plot(0:T0:span, ed, 'LineWidth',1);
xlabel('time/s'),ylabel('e_d');
suptitle('估计误差');
figure(); hold on; grid on;
plot(0:T0:span, y, 'LineWidth',1);
xlabel('time/s'),ylabel('y'); title('输出值');
figure(); hold on; grid on;
plot(0:T0:span, u, 'LineWidth',1);
xlabel('time/s'),ylabel('u'); title('控制量');

采样时间设为0.005s时的结果图：




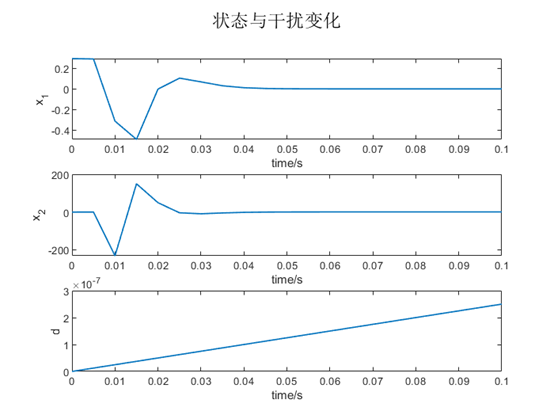
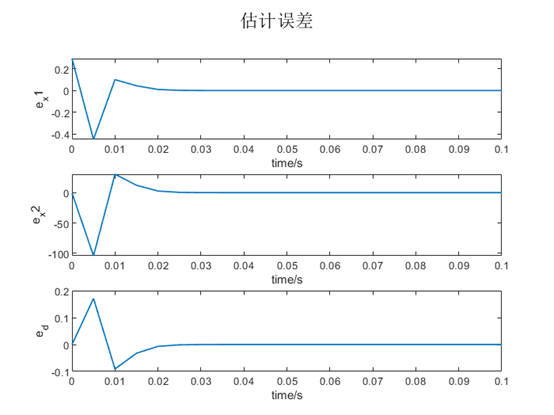
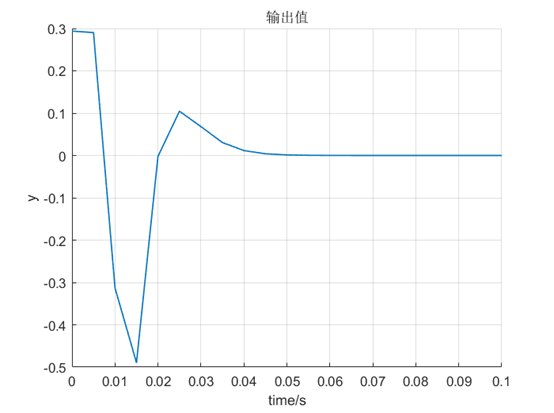
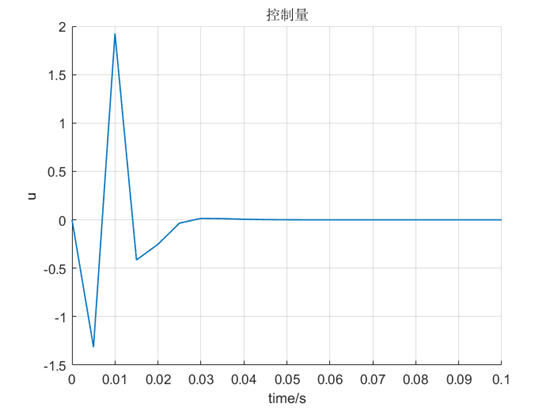
突加幅值为0.1的阶跃扰动后：



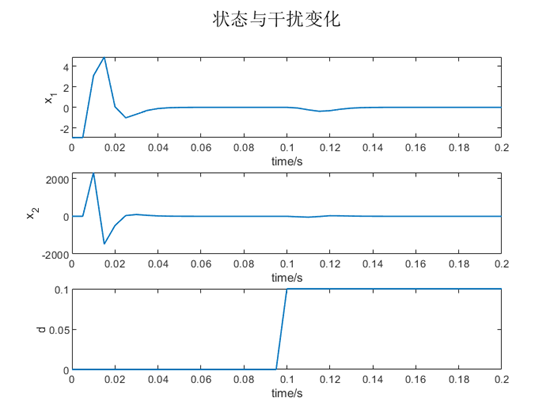
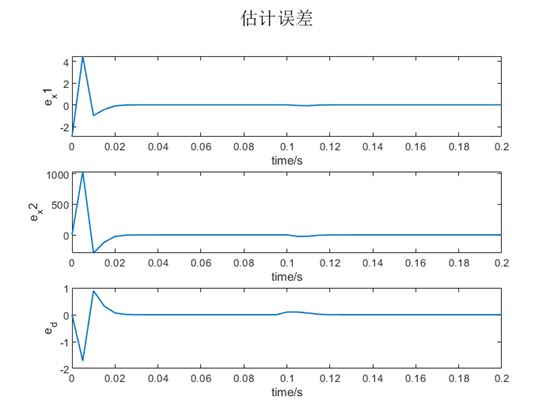
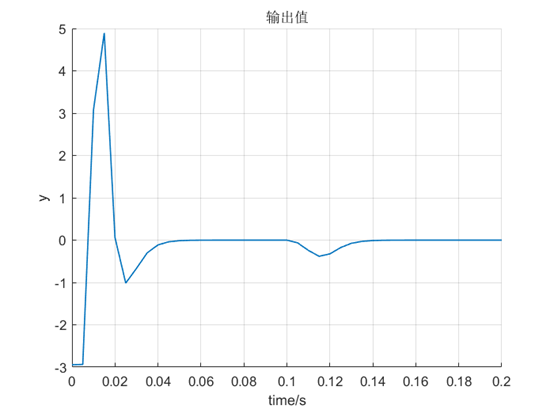
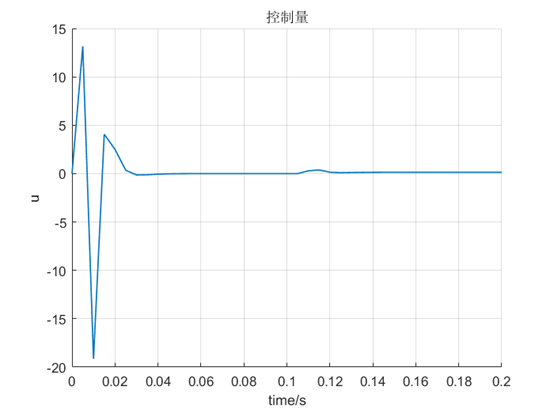
控制效果很好。

参考文献

[1] 张文安,马剑,刑科新.基于广义扩张状态观测器的干扰不匹配离散系统状态反馈控制[J].控制与决策,2016,31(06):1128-1132.

最后

以上就是爱笑乌龟为你收集整理的论文仿真：基于广义扩张状态观测器的干扰不匹配离散系统状态反馈控制参考文献的全部内容，希望文章能够帮你解决论文仿真：基于广义扩张状态观测器的干扰不匹配离散系统状态反馈控制参考文献所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。