现控笔记（二）：状态空间表达式

控制系统状态空间表达式

系统动态过程的两类数学描述：
外部描述：（输入——输出描述）
内部描述：状态空间描述
两个方程描述：状态方程（动态），输出方程（静态）

比较：外部描述不完全，不能反映内部结构的不能控或不能观测部分。

状态空间描述基本概念：
输入：外部对系统的作用（激励），输入包括控制输入和干扰输入。
输出：系统的被控量或从外部测量到的系统信息。
若输出是由传感器测量得到的，又称为观测。

状态变量：一个动力学系统的状态变量组定义为：能完全表征其时间域行为 的一个最小内部变量组。
状态矢量：一个动力学系统的状态定义为由其状态变量组所组成的一个列向 量。
状态空间：状态空间定义为状态向量的一个集合，状态空间的维数等同于状 态的维数。
状态轨线：系统在某个时刻的状态，在状态空间可以看作是一个点。随着时 间的推移，系统状态不断变化，并在状态空间中描述出一条轨迹， 这种轨迹称为状态轨线或状态轨迹。

几点解释：
1.状态变量组对系统行为的完全表征性。给定状态和时间可以确定数值。
2.状态变量组最小性的物理特征。独立储能元件。
3.状态变量组最小性的数学特征。变量组之间线性无关。
4.状态变量组的不唯一性。可选很多个，个数相同。
5.系统任意两个状态变量组之间的关系。
6.有穷维系统和无穷维系统。
7.状态空间的属性。状态空间为建立在实数域R上的一个n维空间。

线性系统状态空间表达式：
描述系统输入、输出和状态变量之间关系的方程组称为系统的状态空间表达式（动态方程或运动方程），包括
状态方程 描述状态变量与输入之间的关系（动态/微分方程）
输出方程 描述输出与状态变量之间的关系（静态/代数方程）
状态 输出
U -----> X -------> Y

画方框图：

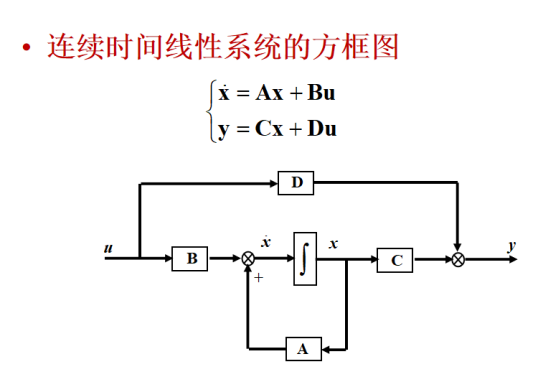
（关键在于积分部分）

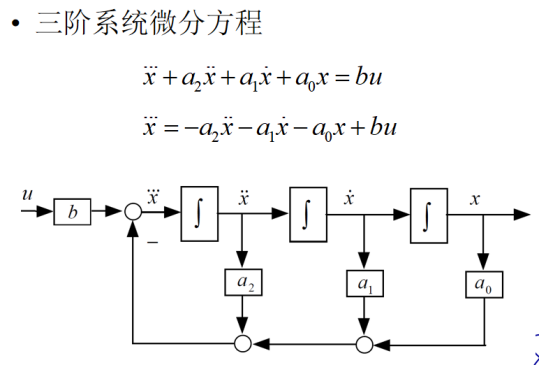
x = x1 x’ = x2 x’’ = x3

1.3
建立状态空间表达式的方法：
从系统结构图建立状态空间表达式
从机理建立状态空间表达式
从传递函数建立状态空间表达式
无零点
有零点
多入多出系统微分方程实现

画系统结构图：
积分环节：

惯性环节：

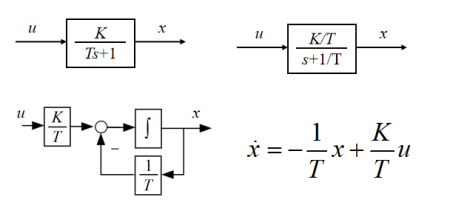
有零点的惯性环节：

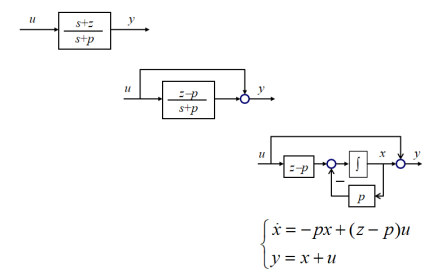
二阶系统：

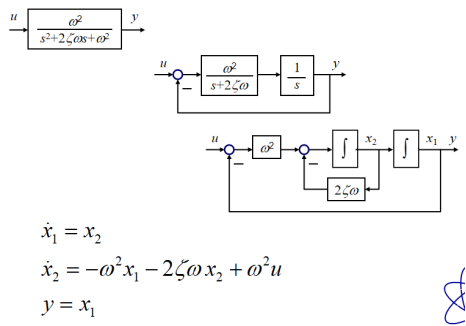
习惯变量定义规则：从最右面的积分号输出开始，x1、x2…

系统输入输出描述导出状态空间描述:
实现是非唯一的，但只要W(s)没有零极点相消则各个实现的阶次相同各个实现都等效于原传递函数。
给定传递函数，求状态空间表达式不唯一。
给定状态空间表达式，求传递函数唯一。

1.4
状态空间表达式建立：

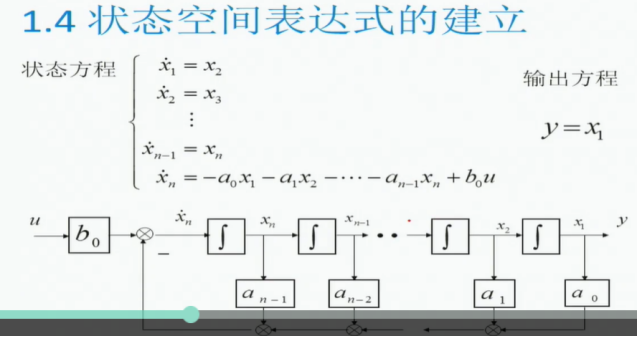
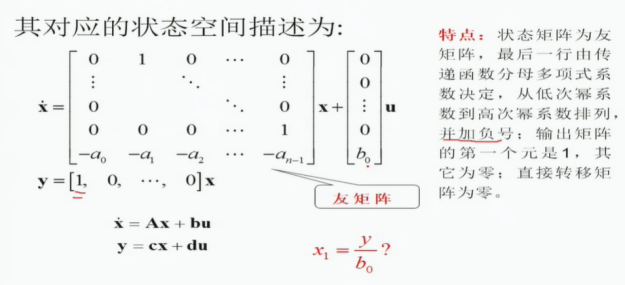
1.5 状态矢量的线性变换

因为状态变量的不同选择，同一个系统具有不同的状态空间模型。
不同的状态变量组之间的关系实质上是一种线性变换的关系，或称坐标变换。

线性时不变系统的特征结构由特征值和特征向量所表征。

特征值：

系统的不变量及系统特征值不变性：
系统矩阵A的一个重要性质是其特征值的不变性，即在状态变量的线性变换中，新老状态方程的系统矩阵的特征值是相同的。

非奇异变换：变换矩阵T通过系统的特征向量求得。

1.状态矩阵A无重特征值时：
如果A有n个两两相异特征值，则存在非奇异矩阵T，通过线性变换，使之化为对角线规范形式。

2. 状态矩阵A有重根时：

特殊形式（标准型）A阵的变换矩阵T：

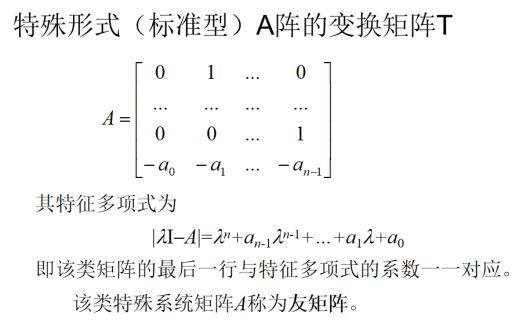
范德蒙矩阵：


（第一列正常，第二列对第一列纵坐标相同元素求导，第三列对第一列纵坐标相同元素求二阶导并乘1/2）

3. 系统的并联型实现

状态方程中系统矩阵为对角线标准型，可见并联实现等价于约旦标准型实现。

1.6 从状态空间表达式求传递函数阵
1.单输入单输出系统

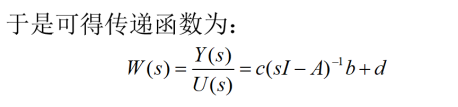
2.多输多输出系统

系统各个输入与输出之间是相互关联的，这种关系称为耦合关系，这是多变量系统的特点。
（adj为矩阵的伴随矩阵）

对于许多复杂的生产过程与设备,其系统结构可以等效为多个子系统的组合结构,这些组合结构可以由3种基本组合联结形式表示：
并联、串联、反馈
1.并联结构：
并联联结组合系统的状态空间模型为：

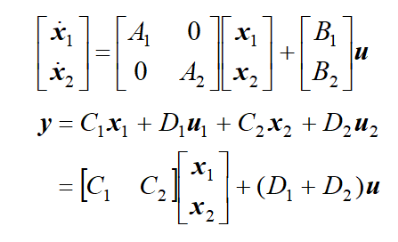
W（s）=W1（s）+ W2（s）

2.串联结构：
串联组合系统的状态空间方程为：

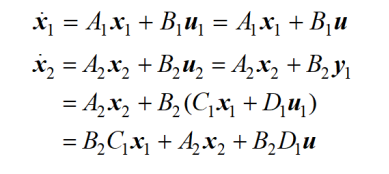
W（s）=W2（s） W1（s）
应当注意,由于矩阵不满足乘法交换律,故在上式中W1(s)和W2(s)的位置不能颠倒,它们的顺序与它们在系统中的串联联结顺序一致。

3. 反馈联结

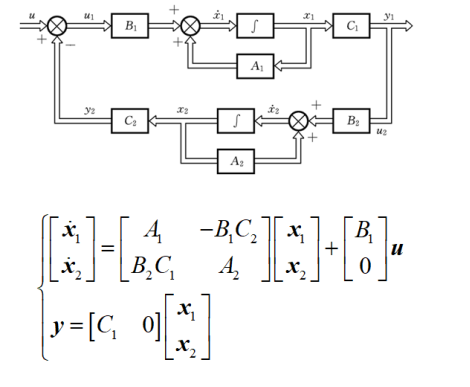
最后

以上就是外向吐司为你收集整理的现控笔记（二）：状态空间表达式的全部内容，希望文章能够帮你解决现控笔记（二）：状态空间表达式所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。