目录
- 一、传递函数 → rightarrow →状态空间模型
- 1.1 预处理
- 1.2 从最简单的分子为1的传递函数入手
- 1.3 分子不为1的传递函数
- 1.4 另一种思路:利用线性叠加原理
- 1.5 对复杂系统使用分解法
- 1.5.1 串联法
- 1.5.2 并联法
- 二、状态空间模型 → rightarrow →传递函数
- 三、对偶关系
- 四、例题
- 五、参考资料
传递函数是经典控制理论的工具,只能用于SISO和LTI系统;状态空间模型属于现代控制理论,对SISO和MIMO、LTI和非线性或时变系统都适用。既然考虑二者的互相转换,那么对象只可能是满足SISO和LTI的系统。
一、传递函数 → rightarrow →状态空间模型
传递函数的一般形式:
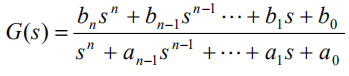
1.1 预处理
用长除法进行简化:
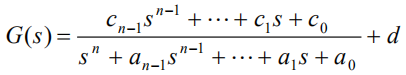
从而得到新的G(s):
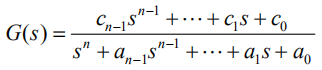
原来的G(s)是新的G(s)和d的并联,可以按并联系统处理。方便起见,下面先只考虑形似新的G(s)的传递函数。
1.2 从最简单的分子为1的传递函数入手
一个例子:
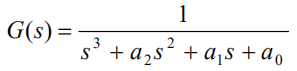
要求它的状态空间模型,首先写成输入输出关系:
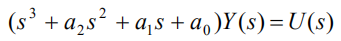
对应的微分方程:
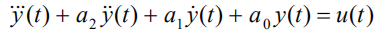
定义新的变量:
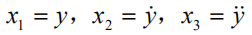
状态空间模型:
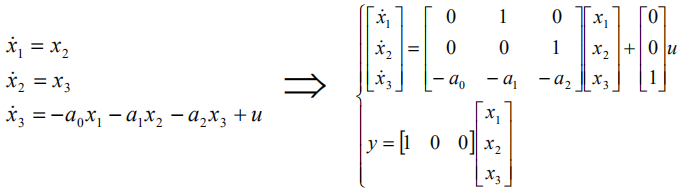
状态矩阵A:最底行对应传递函数分母的系数,符号相反;右上角是2阶单位阵。
输入矩阵B:只有最后一维非零,对应分子常数1。
输出矩阵C:只有第一维非零,1对应分子常数1。
直接转移矩阵D:为0,因为G(s)的分子次数小于分母。
模拟图:
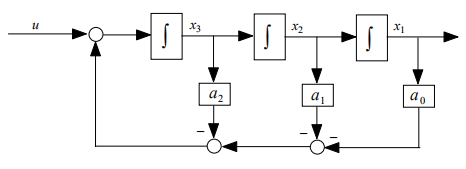
画的时候左边是u,根据B中只有第三维是1,确定u通过加法流向
x
3
˙
dot{x_3}
x3˙,积分得到
x
3
x_3
x3。然后再画
x
2
˙
,
x
2
,
x
1
˙
,
x
1
dot{x_2},x_2,dot{x_1},x_1
x2˙,x2,x1˙,x1。根据
x
3
˙
dot{x_3}
x3˙的构成画反馈。根据C得到
y
=
x
1
y=x_1
y=x1。
根据前面找到的规律,把上面的三阶传递函数,推广到一般情况:
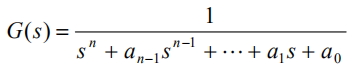
对应的状态空间模型是
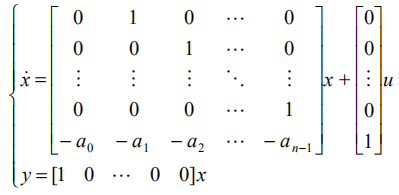
称为是传递函数G的状态空间实现。
1.3 分子不为1的传递函数
还是考虑分母是三阶的:
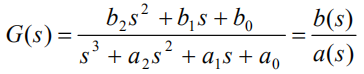
可以看成是:
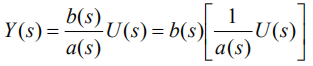
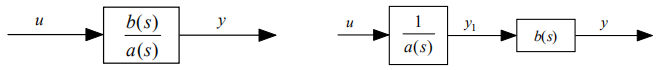
对于内层
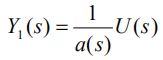
的部分,显然
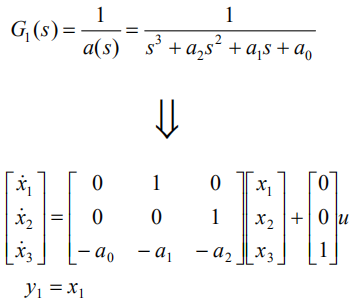
对于外层
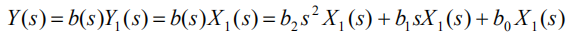
微分方程:
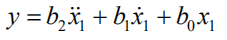
定义状态变量:
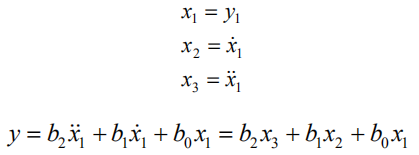
这里的
y
1
y_1
y1也就是分子为1时候的y。也就是说,分子不为1的时候,输出是原来y及其微分的线性组合。所以,对于分子不为1的传函,状态空间模型是
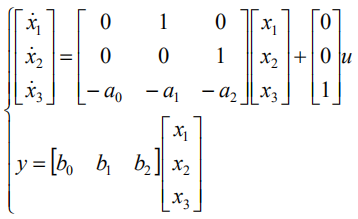
4个矩阵中只有C发生了变化:与传递函数的分子系数相对应。
相应的图为:
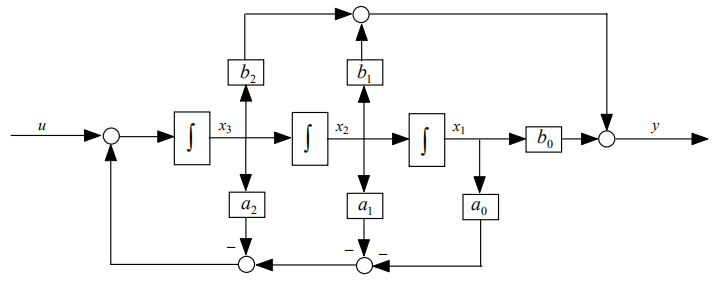
画的时候,将3个积分器的输出线性相加得到最后的输出。
仍然把3维的推广到n维,并且考虑长除法得到的商:
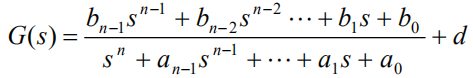
对应的状态空间模型为:
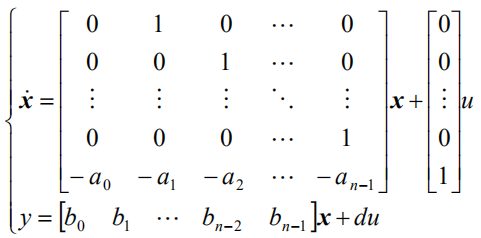
只要把G化成上面的形式,就可以直接观察系数写出模型的4个矩阵了,很方便。这个形式的模型称为“能控标准型”。
1.4 另一种思路:利用线性叠加原理
还是以3阶系统为例:
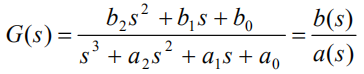
如果直接写成y和u的微分方程:
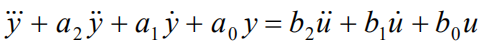
这时候,右边的u是有微分项的(而按1.2中的方法,由于内层的分子是1,避免了这个问题)。
如果先不看微分项,只考虑
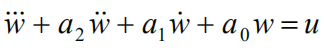
它和前面分析过的分子为1的传递函数是一样的,即有
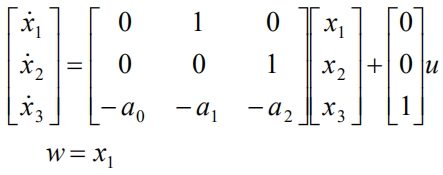
然后只考虑u的一阶微分项作为输入:
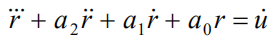
对比上一个方程,可以发现这个方程是上一个方程两边再做一次微分的结果,所以输出分量r和w有这样的关系:
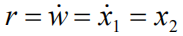
同理,只考虑u的二阶微分的时候:
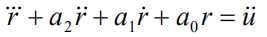
又满足:
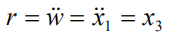
根据叠加原理,总的输出是3个输入分量得到的3个输出分量的线性和:
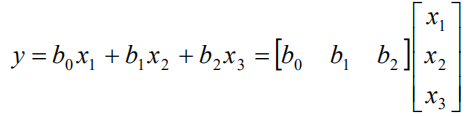
b对应y-u微分方程右边的系数。
1.5 对复杂系统使用分解法
如果G的阶数比较高,可以把它分解成低阶的,先得到低阶的状态空间模型,再合成高阶的模型。可以用串联法、并联法等。
1.5.1 串联法
有的传递函数很容易因式分解,可以用串联法,例如:
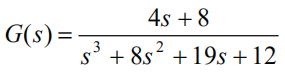
因式分解:
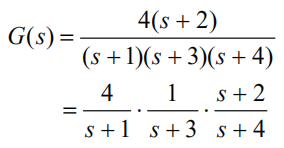
看成是三个环节的串联,很容易得到它们各自的模型:
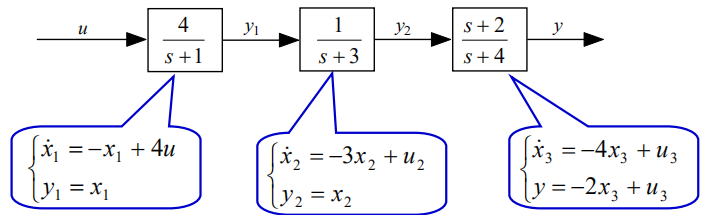
系数的求法用之前的方法就可以做,前两个环节由于阶数很低,熟练之后可以直接看出来。对于第三个环节,我们可以设
X
3
(
s
)
=
1
s
+
4
U
3
(
s
)
X_3(s)=frac{1}{s+4}U_3(s)
X3(s)=s+41U3(s)而
Y
(
s
)
=
(
s
+
2
)
X
3
(
s
)
Y(s)=(s+2)X_3(s)
Y(s)=(s+2)X3(s),即可得:
x
˙
3
=
−
4
x
3
+
u
3
y
=
x
˙
3
+
2
x
3
=
−
4
x
3
+
u
3
+
2
x
3
=
−
2
x
3
+
u
3
begin{aligned} dot{x}_3&=-4x_3+u_3\ y&=dot{x}_3+2x_3\ &=-4x_3+u_3+2x_3\ &=-2x_3+u_3 end{aligned}
x˙3y=−4x3+u3=x˙3+2x3=−4x3+u3+2x3=−2x3+u3
这三个环节有什么关联呢?u2=y1,u3=y2。所以
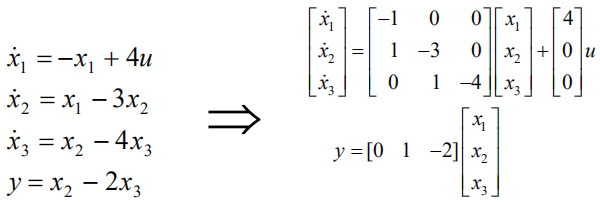
图:
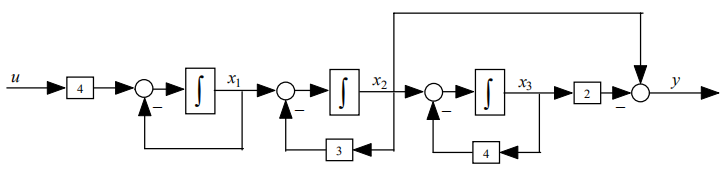
1.5.2 并联法
考虑
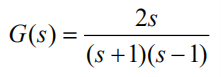
分解得到
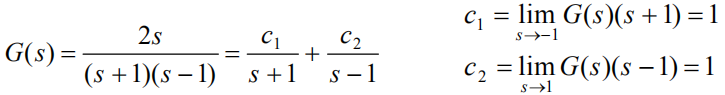
画图,分别求出两个环节的模型:
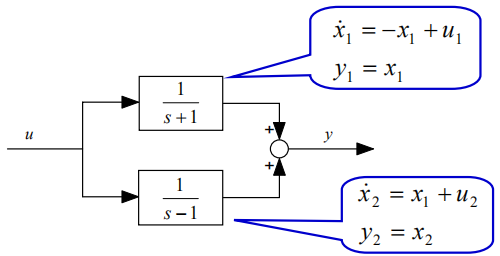
对于并联,两个环节之间的关系是:u=u1=u2,y=y1+y2。因此
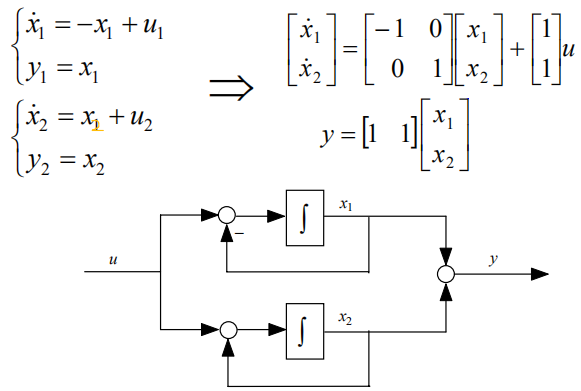
这里的A是对角阵,所以并联得到的也称“对角型”。
系数的规律:
A中的系数值是传递函数极点-1和1,B的系数对应分子1和1。
实际上,对于
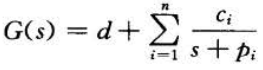
利用并联法得到的模型为:

状态图:
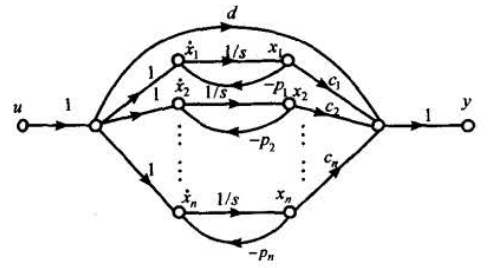
如果存在重极点,例如:
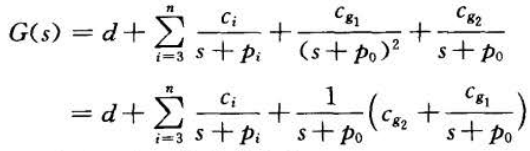
系数用留数定理求:
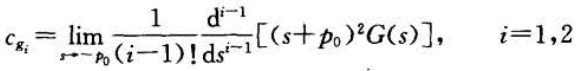
输入输出关系为:
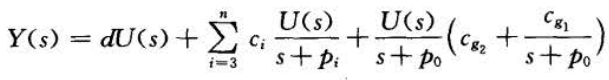
令
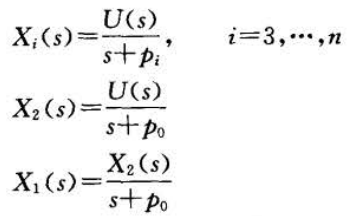
得到系统状态方程和输出方程:
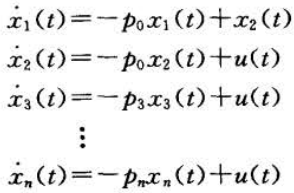
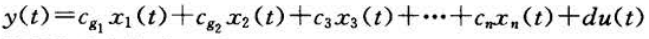
因此,模型为:

观察发现,如果存在重根,则A为若当型,n重根对应的若当块是n阶的,并且相应的B中的系数为0。
状态图为:
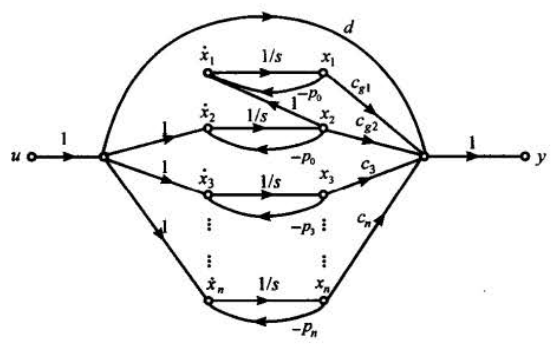
二、状态空间模型 → rightarrow →传递函数
设已知的状态空间模型为:
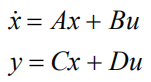
在零初始条件下,用拉普拉斯变换得到
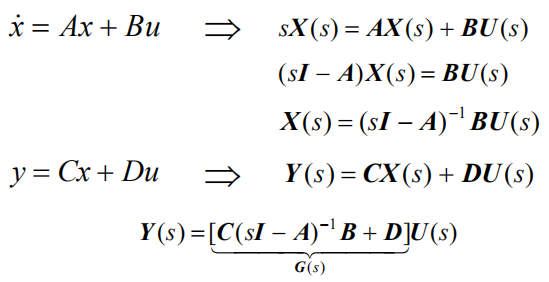
所以
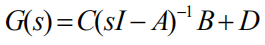
可见,传递函数是由状态空间模型唯一确定的。
三、对偶关系
在2中根据状态空间模型可以求出传递函数:
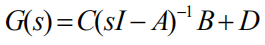
对于SISO系统,这是一个标量,所以,
G
=
G
T
G=G^T
G=GT。由此,可以得到:
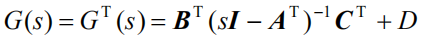
这两种写法的形式是一样的,对比系数可以得出另一种模型写法:
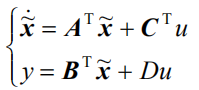
这种写法的模型被称为原来模型的对偶系统模型。
对这个对偶模型再做一次对偶,可以得到原来的模型
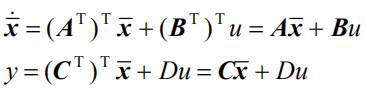
这说明对偶关系是双向的,它们互为对偶。
我们上面写过能控标准型:
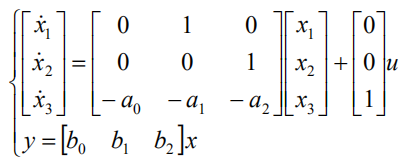
它也有它的对偶模型,即“能观标准型”:
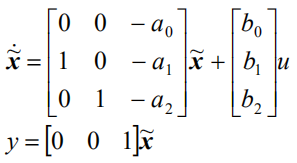
两种模型的状态图:
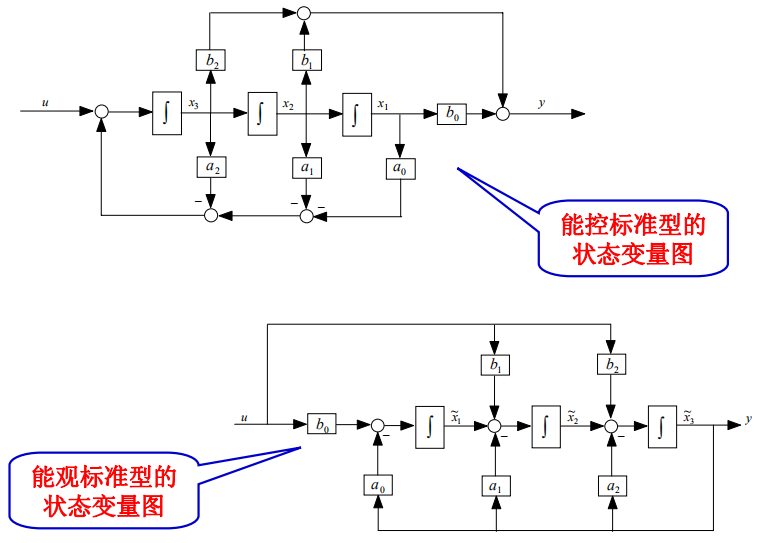
四、例题

五、参考资料
[1] 浙江工业大学俞立老师课程ppt,网课见b站:现代控制理论 浙江工业大学 俞立,评论区有ppt的网盘链接
[2] 田玉平,蒋珉,李世华.自动控制原理[M].北京:科学出版社,2006
最后
以上就是紧张大门最近收集整理的关于状态空间模型与传递函数的转换关系+例题一、传递函数 → \rightarrow →状态空间模型二、状态空间模型 → \rightarrow →传递函数三、对偶关系四、例题五、参考资的全部内容,更多相关状态空间模型与传递函数的转换关系+例题一、传递函数 内容请搜索靠谱客的其他文章。








发表评论 取消回复