数字信号处理学习笔记（三）|时域离散系统的网络结构

时域离散系统的网络结构

一、何为网络结构

网络结构如同差分方程、单位脉冲响应以及系统函数一样，描述了一个系统实现方法的表达形式。
例如给定一个差分方程：y(n)=0.8y(n-1)-0.15y(n-2)+x(n),我们可以把系统函数分解为三种形式：直接型，并联型、级联型。

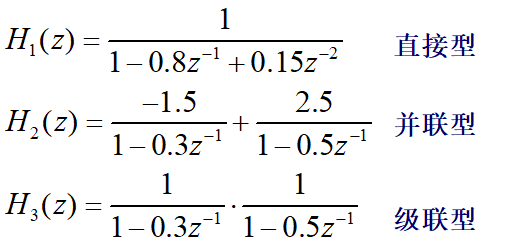
网络结构表示一定的运算结构，而不同的结构的运算复杂程度、运算速度、运算误差是不同的，对于实现信号处理的网络结构是很重要的。

二、用信号流图表示网络结构

1、乘法器、加法器、单位延迟器

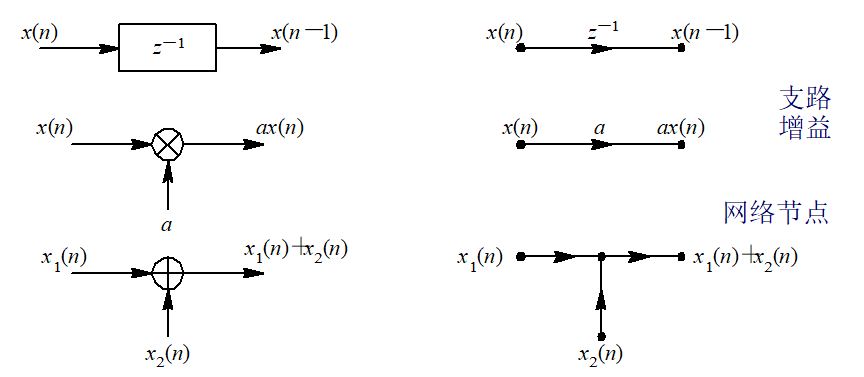
支路的值=支路起点处的节点值*传输系数
节点的值=所有输入支路的值之和

2、基本信号流图

不同的信号流而同一个代表不同的算法，而同一个系统函数可以有很多种信号流图相对应。满足一下条件，称为基本信号流图：
1、信号流图中所有支路都是基本的， 即支路增益是常数或者z^-1.
2、流图环路中必须存在延时支路
3、节点和支路的数目是有限的

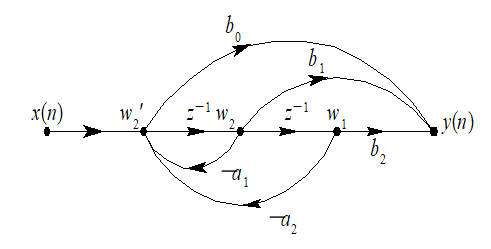
三、直接型网络结构

若一个H(z)为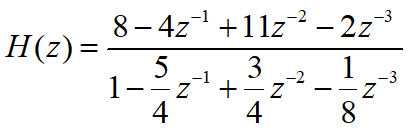
写出差分方程如下：

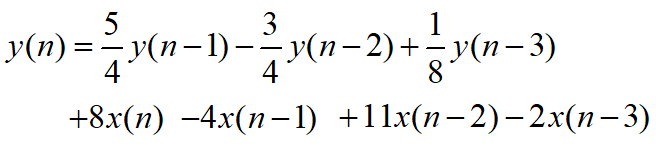
再画出直接型结构：

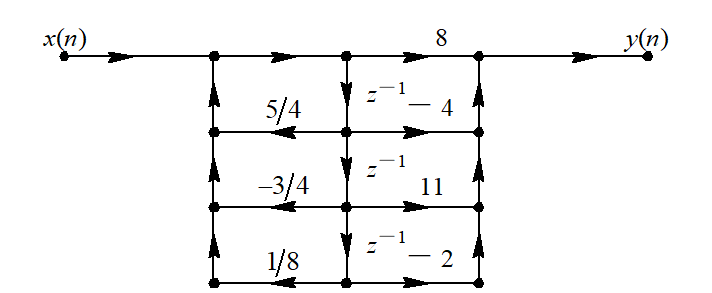
直接型的优点：
可直接由传递函数或差分方程直接画出网络结构流图

直接型的缺点：
1.系数a、b对网络的性能控制作用不明显，调整零极点困难
2、极点对系数的变化过于灵敏，易出现不稳定或较大误差
3、运算的累计误差较大

四、级联型

一个系统函数如下：

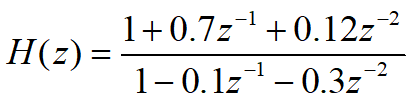
将分母分子因式分解得到：

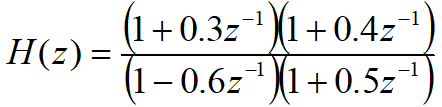
整理一下：

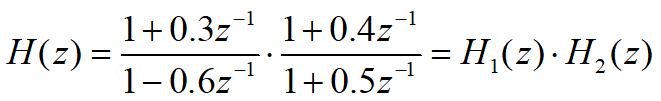
得到级联型流图：

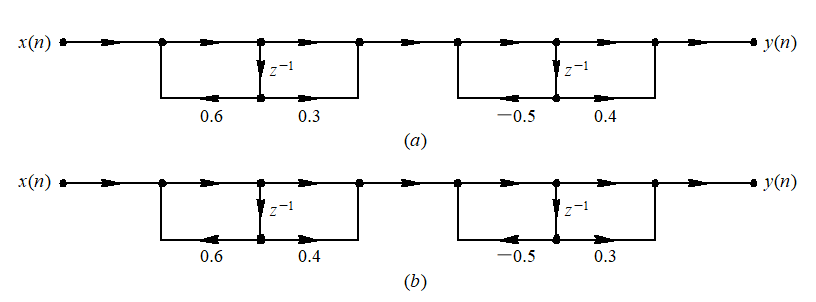
级联型的特点
1、调整系数能单独调整滤波器的第n对零或极点，不影响其他零极点
2、便于调整滤波器频率响应性能
3、运算的累积误差较小
4、具有最少的存储器

五、并联型

H(z)如下：

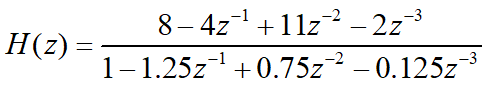
将H(z)展开成部分分式：

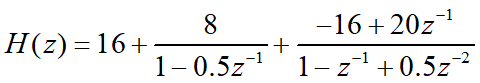
每一部分用直接型结构实现：

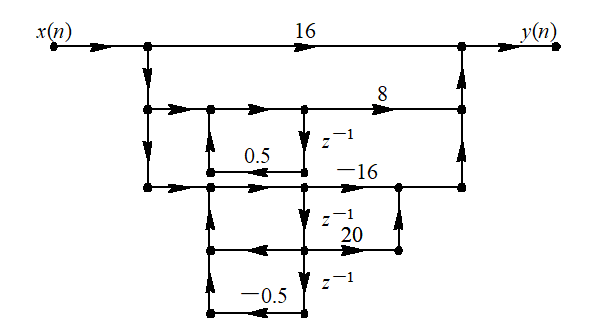
并联型特点：
1、能通过调整系数单独调整一对极点位置，但不能单独调整零点位置
2、个并联节点的误差互相不影响，运算误差最小
3、可同时对输入信号进行运算，运算速度最高

最后

以上就是平淡绿茶为你收集整理的数字信号处理学习笔记（三）|时域离散系统的网络结构的全部内容，希望文章能够帮你解决数字信号处理学习笔记（三）|时域离散系统的网络结构所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。