三维数学--欧拉角与四元数

欧拉角(EulerAngle)

欧拉角就是物体绕坐标系三个坐标轴(x,y,z轴）的旋转角度。

欧拉角可分为两种情况：

1，静态：即绕世界坐标系三个轴的旋转，由于物体旋转过程中坐标轴保持静止，所以称为静态。

2，动态：即绕物体坐标系三个轴的旋转，由于物体旋转过程中坐标轴随着物体做相同的转动，所以称为动态。

笛卡尔坐标系
heading-pitch-bank，分别物体表示绕Y轴X轴和Z轴的旋转,即绕y轴旋转为heading，绕x轴旋转为pitch，绕z轴旋转为bank。

万向锁问题
对于动态欧拉角，即绕物体坐标系旋转。（静态不存在万向锁的问题）无论heading和bank为多少度，
只要pitch为±90°（即绕第二个轴的旋转），就会出现万向锁现象。
(x角度为90(x轴旋转±90度) 自身坐标系z轴与世界坐标系y轴重合，失去一个自由度)

万向锁的避免问题：限制旋转的角度范围
heading-pitch-bank
heading 绕Y轴 限制范围在±180°
pitch 绕X轴 限制范围在±90°
bank 绕Z轴 限制范围在±180°

四元数(Quaternion)

在计算机图形学中，四元数用于物体的旋转

对于一个物体的旋转，其实我们只需要知道四个值：一个旋转的向量 + 一个旋转的角度，其中x,y,z 代表的是向量的三维坐标，w代表的是角度

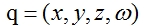
四元数角度范围:0~360°。

这里简单的说一下利用四元数来做旋转的方式：

现在我们有一个向量：v1，要让它绕 v2 旋转 Θ 度，我们先把这个向量写成一个四元数：p = (v1, 0); 那么旋转的四元数则是：q = ( v2 * sin(θ/2) , cos(θ/2) ) ;旋转后的四元数为（得到的四元数实部为0，虚部为新的坐标）：

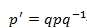
尝试训练：把点P(1, 0, 1)绕旋转轴u = (0, 1, 0)旋转90°，求旋转后的顶点坐标。首先将P扩充到四元数，即p = (P, 0)。而q = (u*sin45°, cos45°)。求p′=qpq−1的值。建议大家一定要在纸上计算一边，这样才能加深印象。最后的结果p` = ((1, 0, -1), 0)，即旋转后的顶点位置是(1, 0, -1)。

欧拉角与四元数对比优缺点

欧拉旋转

优点：
很容易理解，形象直观；
表示更方便，只需要3个值(分别对应x, y, z轴的旋转角度)。

缺点：
之前提到过这种方法是要按照一个固定的坐标轴的顺序旋转的，因此不同的顺序会造成不同的结果，会造成万向节锁(Gimbal Lock) 现象。这种现象的发生就是由于上述固定坐标轴旋转顺序造成的。
理论上，欧拉选择可以靠这种顺序让一个物体指到任何一个想要的方向，但如果在旋转中不幸让某些坐标轴重合了就会发生万向节锁，这时候就会丢失一个方向上的旋转能力，也就是说在这种状态下我们无论怎么旋转（当然还是按照原先的顺序）都不可能得到某些想要的旋转效果，除非我们打破原先的旋转顺序或者同时旋转3个坐标轴。这里有个欧拉旋转可以直观的理解下；
由于万向节锁的存在，欧拉旋转无法实现球面平滑插值。

四元数旋转

优点：
可以避免万向节锁现象；
只需要一个4维的四元数就可以执行绕任意过原点的向量的旋转，方便快捷，在某些实现下比旋转矩阵效率更高；
可以提供平滑插值。

缺点：
比欧拉选择稍微复杂了一点点，因为多了一个维度；
理解更困难，不直观。

最后

以上就是舒服枕头为你收集整理的三维数学--欧拉角与四元数的全部内容，希望文章能够帮你解决三维数学--欧拉角与四元数所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。