1. 首页
  2. 文章中心
  3. Other

四元素与欧拉角

93 阅读 0 评论
我是靠谱客的博主 凶狠雪糕，这篇文章主要介绍四元素与欧拉角，现在分享给大家，希望可以做个参考。

RPY角与Z-Y-X欧拉角

　　描述坐标系{B}相对于参考坐标系{A}的姿态有两种方式。第一种是绕固定（参考）坐标轴旋转：假设开始两个坐标系重合，先将{B}绕{A}的X轴旋转γγ，然后绕{A}的Y轴旋转ββ，最后绕{A}的Z轴旋转αα，就能旋转到当前姿态。可以称其为X-Y-Z fixed angles或RPY角(Roll, Pitch, Yaw)。

　　Roll:横滚

　　Pitch: 俯仰

Yaw: 偏航（航向）

　　由于是绕固定坐标系旋转，则旋转矩阵为（cαcα is shorthand for cosαcos⁡α, sαsα is shorthand for sinαsin⁡α,and so on.）

RXYZ(γ,β,α)=RZ(α)RY(β)RX(γ)=⎡⎣⎢cαcβsαcβ−sβcαsβsγ−sαcγsαsβsγ+cαcγcβsγcαsβcγ+sαsγsαsβcγ−cαsγcβcγ⎤⎦⎥RXYZ(γ,β,α)=RZ(α)RY(β)RX(γ)=[cαcβcαsβsγ−sαcγcαsβcγ+sαsγsαcβsαsβsγ+cαcγsαsβcγ−cαsγ−sβcβsγcβcγ]

　　另一种姿态描述方式是绕自身坐标轴旋转：假设开始两个坐标系重合，先将{B}绕自身的Z轴旋转αα，然后绕Y轴旋转ββ，最后绕X轴旋转γγ，就能旋转到当前姿态。称其为Z-Y-X欧拉角，由于是绕自身坐标轴进行旋转，则旋转矩阵为：

RZ′Y′X′(α,β,γ)=RZ(α)RY(β)RX(γ)=⎡⎣⎢cαcβsαcβ−sβcαsβsγ−sαcγsαsβsγ+cαcγcβsγcαsβcγ+sαsγsαsβcγ−cαsγcβcγ⎤⎦⎥RZ′Y′X′(α,β,γ)=RZ(α)RY(β)RX(γ)=[cαcβcαsβsγ−sαcγcαsβcγ+sαsγsαcβsαsβsγ+cαcγsαsβcγ−cαsγ−sβcβsγcβcγ]

　　可以发现这两种描述方式得到的旋转矩阵是一样的，即绕固定坐标轴X-Y-Z旋转(γ,β,α)(γ,β,α)和绕自身坐标轴Z-Y-X旋转(α,β,γ)(α,β,γ)的最终结果一样，只是描述的方法有差别而已。In gerenal: three rotations taken about fixed axes yield the same final orientation as the same three rotations taken in opposite order about the axes of the moving frame.

  • Axis-Angle与四元数

　　绕坐标轴的多次旋转可以等效为绕某一转轴旋转一定的角度。假设等效旋转轴方向向量为K⃗=[kx,ky,kz]TK→=[kx,ky,kz]T，等效旋转角为θθ，则四元数q=(x,y,z,w)q=(x,y,z,w)，其中：

xyzw=kx⋅sinθ2=ky⋅sinθ2=kz⋅sinθ2=cosθ2x=kx⋅sinθ2y=ky⋅sinθ2z=kz⋅sinθ2w=cosθ2

　　且有x2+y2+z2+w2=1x2+y2+z2+w2=1

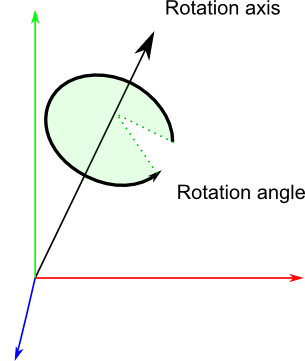
　　即四元数存储了旋转轴和旋转角的信息，它能方便的描述刚体绕任意轴的旋转。

四元数转换为旋转矩阵：

R=⎡⎣⎢1−2y2−2z22(xy+zw)2(xz−yw)2(xy−zw)1−2x2−2z22(yz+xw)2(xz+yw)2(yz−xw)1−2x2−2y2⎤⎦⎥R=[1−2y2−2z22(xy−zw)2(xz+yw)2(xy+zw)1−2x2−2z22(yz−xw)2(xz−yw)2(yz+xw)1−2x2−2y2]

 　　已知旋转矩阵为：

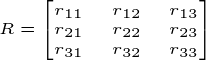
　　则对应的四元数为：

 

 

  • 四元数与欧拉角的相互转换

　　定义两个四元数：

　　
　　
　　其中 表示矢量
 
；而
 
表示矢量
 

四元数加法：

　　跟复数、向量和矩阵一样，两个四元数之和需要将不同的元素加起来。
　　加法遵循实数和复数的所有交换律和结合律。

四元数乘法：

　　四元数的乘法的意义类似于矩阵的乘法，可以表示旋转的合成。当有多次旋转操作时，使用四元数可以获得更高的计算效率。

　　由于四元数乘法的非可换性，pq并不等于qp，qp乘积的向量部分是：
　　
　　Mathematica中有四元数相关的程序包Quaternions Package，需要先导入才能使用。下面计算了三个四元数的乘积：
　　Mathematica中有四元数相关的程序包Quaternions Package，需要先导入才能使用。下面计算了三个四元数的乘积：
复制代码
1
2
<<Quaternions`     （* This loads the package *）
Quaternion[2, 1, 1, 3] ** Quaternion[2, 1, 1, 0] ** Quaternion[1, 1, 1, 1]    (* Be sure to use ** rather than * when multiplying quaternions *)

　　计算结果为：Quaternion[-12, 4, 14, 2]

 
　　那么将Z-Y-X欧拉角（或RPY角：绕固定坐标系的X-Y-Z依次旋转αα,ββ,γγ角）转换为四元数：

q=⎡⎣⎢⎢⎢⎢⎢cosγ200sinγ2⎤⎦⎥⎥⎥⎥⎥⎡⎣⎢⎢⎢⎢⎢cosβ20sinβ20⎤⎦⎥⎥⎥⎥⎥⎡⎣⎢⎢⎢⎢cosα2sinα200⎤⎦⎥⎥⎥⎥=⎡⎣⎢⎢⎢⎢⎢⎢⎢cosα2cosβ2cosγ2+sinα2sinβ2sinγ2sinα2cosβ2cosγ2−cosα2sinβ2sinγ2cosα2sinβ2cosγ2+sinα2cosβ2sinγ2cosα2cosβ2sinγ2−sinα2sinβ2cosγ2⎤⎦⎥⎥⎥⎥⎥⎥⎥q=[cos⁡γ200sin⁡γ2][cos⁡β20sin⁡β20][cos⁡α2sin⁡α200]=[cos⁡α2cos⁡β2cos⁡γ2+sin⁡α2sin⁡β2sin⁡γ2sin⁡α2cos⁡β2cos⁡γ2−cos⁡α2sin⁡β2sin⁡γ2cos⁡α2sin⁡β2cos⁡γ2+sin⁡α2cos⁡β2sin⁡γ2cos⁡α2cos⁡β2sin⁡γ2−sin⁡α2sin⁡β2cos⁡γ2]

 　　根据上面的公式可以求出逆解，即由四元数q=(q0,q1,q2,q3)q=(q0,q1,q2,q3)或q=(w,x,y,z)q=(w,x,y,z)到欧拉角的转换为：

⎡⎣⎢αβγ⎤⎦⎥=⎡⎣⎢⎢⎢⎢arctan2(q0q1+q2q3)1−2(q21+q22)arcsin(2(q0q2−q1q3))arctan2(q0q3+q1q2)1−2(q22+q23)⎤⎦⎥⎥⎥⎥[αβγ]=[arctan⁡2(q0q1+q2q3)1−2(q12+q22)arcsin⁡(2(q0q2−q1q3))arctan⁡2(q0q3+q1q2)1−2(q22+q32)]

　　由于arctan和arcsin的取值范围在−π2−π2和π2π2之间，只有180°，而绕某个轴旋转时范围是360°，因此要使用atan2函数代替arctan函数：

⎡⎣⎢αβγ⎤⎦⎥=⎡⎣⎢atan2(2(q0q1+q2q3),1−2(q21+q22))arcsin(2(q0q2−q1q3))atan2(2(q0q3+q1q2),1−2(q22+q23))⎤⎦⎥[αβγ]=[atan2(2(q0q1+q2q3),1−2(q12+q22))arcsin⁡(2(q0q2−q1q3))atan2(2(q0q3+q1q2),1−2(q22+q32))]

对于tan(θ) = y / x ：

　　θ = ATan(y / x)求出的θ取值范围是[-PI/2, PI/2]；

　　θ = ATan2(y, x)求出的θ取值范围是[-PI,   PI]。

  • 当 (x, y) 在第一象限, 0 < θ < PI/2

  • 当 (x, y) 在第二象限 PI/2 < θ≤PI

  • 当 (x, y) 在第三象限, -PI < θ < -PI/2

  • 当 (x, y) 在第四象限, -PI/2 < θ < 0

 　　将四元数转换为欧拉角可以参考下面的代码。需要注意欧拉角有12种旋转次序，而上面推导的公式是按照Z-Y-X顺序进行的，所以有时会在网上看到不同的转换公式（因为对应着不同的旋转次序），在使用时一定要注意旋转次序是什么。比如ADAMS软件里就默认Body 3-1-3次序，即Z-X-Z欧拉角，而VREP中则按照X-Y-Z欧拉角旋转。
复制代码
1
enum RotSeq{zyx, zyz, zxy, zxz, yxz, yxy, yzx, yzy, xyz, xyx, xzy,xzx};
复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
// COMPILE: g++ -o quat2EulerTest quat2EulerTest.cpp 
#include <iostream>
#include <cmath> 

using namespace std;

///
// Quaternion struct
// Simple incomplete quaternion struct for demo purpose
///
struct Quaternion{
  Quaternion():x(0), y(0), z(0), w(1){};
  Quaternion(double x, double y, double z, double w):x(x), y(y), z(z), w(w){};
 
  void normalize(){
    double norm = std::sqrt(x*x + y*y + z*z + w*w);
    x /= norm;
    y /= norm;
    z /= norm;
    w /= norm;
  }
  
  double norm(){
    return std::sqrt(x*x + y*y + z*z + w*w);
  }

  double x;
  double y;
  double z;
  double w;  
  
};

///
// Quaternion to Euler
///
enum RotSeq{zyx, zyz, zxy, zxz, yxz, yxy, yzx, yzy, xyz, xyx, xzy,xzx};

void twoaxisrot(double r11, double r12, double r21, double r31, double r32, double res[]){
  res[0] = atan2( r11, r12 );
  res[1] = acos ( r21 );
  res[2] = atan2( r31, r32 );
}
    
void threeaxisrot(double r11, double r12, double r21, double r31, double r32, double res[]){
  res[0] = atan2( r31, r32 );
  res[1] = asin ( r21 );
  res[2] = atan2( r11, r12 );
}

void quaternion2Euler(const Quaternion& q, double res[], RotSeq rotSeq)
{
    switch(rotSeq){
    case zyx:
      threeaxisrot( 2*(q.x*q.y + q.w*q.z),
                     q.w*q.w + q.x*q.x - q.y*q.y - q.z*q.z,
                    -2*(q.x*q.z - q.w*q.y),
                     2*(q.y*q.z + q.w*q.x),
                     q.w*q.w - q.x*q.x - q.y*q.y + q.z*q.z,
                     res);
      break;
    
    case zyz:
      twoaxisrot( 2*(q.y*q.z - q.w*q.x),
                   2*(q.x*q.z + q.w*q.y),
                   q.w*q.w - q.x*q.x - q.y*q.y + q.z*q.z,
                   2*(q.y*q.z + q.w*q.x),
                  -2*(q.x*q.z - q.w*q.y),
                  res);
      break;
                
    case zxy:
      threeaxisrot( -2*(q.x*q.y - q.w*q.z),
                      q.w*q.w - q.x*q.x + q.y*q.y - q.z*q.z,
                      2*(q.y*q.z + q.w*q.x),
                     -2*(q.x*q.z - q.w*q.y),
                      q.w*q.w - q.x*q.x - q.y*q.y + q.z*q.z,
                      res);
      break;

    case zxz:
      twoaxisrot( 2*(q.x*q.z + q.w*q.y),
                  -2*(q.y*q.z - q.w*q.x),
                   q.w*q.w - q.x*q.x - q.y*q.y + q.z*q.z,
                   2*(q.x*q.z - q.w*q.y),
                   2*(q.y*q.z + q.w*q.x),
                   res);
      break;

    case yxz:
      threeaxisrot( 2*(q.x*q.z + q.w*q.y),
                     q.w*q.w - q.x*q.x - q.y*q.y + q.z*q.z,
                    -2*(q.y*q.z - q.w*q.x),
                     2*(q.x*q.y + q.w*q.z),
                     q.w*q.w - q.x*q.x + q.y*q.y - q.z*q.z,
                     res);
      break;

    case yxy:
      twoaxisrot( 2*(q.x*q.y - q.w*q.z),
                   2*(q.y*q.z + q.w*q.x),
                   q.w*q.w - q.x*q.x + q.y*q.y - q.z*q.z,
                   2*(q.x*q.y + q.w*q.z),
                  -2*(q.y*q.z - q.w*q.x),
                  res);
      break;
      
    case yzx:
      threeaxisrot( -2*(q.x*q.z - q.w*q.y),
                      q.w*q.w + q.x*q.x - q.y*q.y - q.z*q.z,
                      2*(q.x*q.y + q.w*q.z),
                     -2*(q.y*q.z - q.w*q.x),
                      q.w*q.w - q.x*q.x + q.y*q.y - q.z*q.z,
                      res);
      break;

    case yzy:
      twoaxisrot( 2*(q.y*q.z + q.w*q.x),
                  -2*(q.x*q.y - q.w*q.z),
                   q.w*q.w - q.x*q.x + q.y*q.y - q.z*q.z,
                   2*(q.y*q.z - q.w*q.x),
                   2*(q.x*q.y + q.w*q.z),
                   res);
      break;

    case xyz:
      threeaxisrot( -2*(q.y*q.z - q.w*q.x),
                    q.w*q.w - q.x*q.x - q.y*q.y + q.z*q.z,
                    2*(q.x*q.z + q.w*q.y),
                   -2*(q.x*q.y - q.w*q.z),
                    q.w*q.w + q.x*q.x - q.y*q.y - q.z*q.z,
                    res);
      break;
        
    case xyx:
      twoaxisrot( 2*(q.x*q.y + q.w*q.z),
                  -2*(q.x*q.z - q.w*q.y),
                   q.w*q.w + q.x*q.x - q.y*q.y - q.z*q.z,
                   2*(q.x*q.y - q.w*q.z),
                   2*(q.x*q.z + q.w*q.y),
                   res);
      break;
        
    case xzy:
      threeaxisrot( 2*(q.y*q.z + q.w*q.x),
                     q.w*q.w - q.x*q.x + q.y*q.y - q.z*q.z,
                    -2*(q.x*q.y - q.w*q.z),
                     2*(q.x*q.z + q.w*q.y),
                     q.w*q.w + q.x*q.x - q.y*q.y - q.z*q.z,
                     res);
      break;
        
    case xzx:
      twoaxisrot( 2*(q.x*q.z - q.w*q.y),
                   2*(q.x*q.y + q.w*q.z),
                   q.w*q.w + q.x*q.x - q.y*q.y - q.z*q.z,
                   2*(q.x*q.z + q.w*q.y),
                  -2*(q.x*q.y - q.w*q.z),
                  res);
      break;
    default:
      std::cout << "Unknown rotation sequence" << std::endl;
      break;
   }
}

///
// Helper functions
///
Quaternion operator*(Quaternion& q1, Quaternion& q2){
  Quaternion q;
  q.w = q1.w*q2.w - q1.x*q2.x - q1.y*q2.y - q1.z*q2.z;
  q.x = q1.w*q2.x + q1.x*q2.w + q1.y*q2.z - q1.z*q2.y;
  q.y = q1.w*q2.y - q1.x*q2.z + q1.y*q2.w + q1.z*q2.x;
  q.z = q1.w*q2.z + q1.x*q2.y - q1.y*q2.x + q1.z*q2.w;
  return q;
}

ostream& operator <<(std::ostream& stream, const Quaternion& q) {
  cout << q.w << " "<< showpos << q.x << "i " << q.y << "j " << q.z << "k"; 
  cout << noshowpos;
}

double rad2deg(double rad){
  return rad*180.0/M_PI;
}

///
// Main
///
int main(){

  Quaternion q; // x,y,z,w
  Quaternion qx45(sin(M_PI/8), 0,0, cos(M_PI/8) );
  Quaternion qy45(0, sin(M_PI/8), 0, cos(M_PI/8));
  Quaternion qz45(0, 0, sin(M_PI/8), cos(M_PI/8));
  Quaternion qx90(sin(M_PI/4), 0,0, cos(M_PI/4) );
  Quaternion qy90(0, sin(M_PI/4), 0, cos(M_PI/4));
  Quaternion qz90(0, 0, sin(M_PI/4), cos(M_PI/4));

  double res[3];

  q = qz45*qx45;
  q.normalize();
  quaternion2Euler(q, res, zyx);
  cout << "Rotation sequence: X->Y->Z" << endl;
  cout << "x45 -> z45" << endl;
  cout << "q: " << q << endl;
  cout << "x: " << rad2deg(res[0]) << " y: " << rad2deg(res[1]) << " z: " << rad2deg(res[2]) << endl << endl;

  q = qz90*qx90;
  q.normalize();
  quaternion2Euler(q, res, zyx);
  cout << "Rotation sequence: X->Y->Z" << endl;
  cout << "x90 -> z90" << endl;
  cout << "q: " << q << endl;
  cout << "x: " << rad2deg(res[0]) << " y: " << rad2deg(res[1]) << " z: " << rad2deg(res[2]) << endl << endl;

  q = qx90*qz90;
  q.normalize();
  quaternion2Euler(q, res, xyz);
  cout << "Rotation sequence: Z->Y->X" << endl;
  cout << "z90 -> x90" << endl;
  cout << "q: " << q << endl;
  cout << "x: " << rad2deg(res[0]) << " y: " << rad2deg(res[1]) << " z: " << rad2deg(res[2]) << endl;
}
View Code

　　 上面的代码存在一个问题，即奇异性没有考虑。下面看一种特殊的情况（参考Maths - Conversion Quaternion to Euler）：假设一架飞机绕Y轴旋转了90°（俯仰角pitch=90），机头垂直向上，此时如何计算航向角和横滚角？

　　这时会发生自由度丢失的情况，即Yaw和Roll会变为一个自由度。此时再使用上面的公式根据四元数计算欧拉角会出现问题：

　　arcsin(2(q0q2−q1q3))arcsin⁡(2(q0q2−q1q3))的定义域为[−1,1][−1,1]，因此(q0q2−q1q3)∈[−0.5,0.5](q0q2−q1q3)∈[−0.5,0.5]，当q0q2−q1q3=0.5q0q2−q1q3=0.5时（在程序中浮点数不能直接进行等于判断，要使用合理的阈值），俯仰角ββ为90°，将其带入正向公式计算出四元数(q0,q1,q2,q3)(q0,q1,q2,q3)，然后可以发现逆向公式中atan2函数中的参数全部为0，即出现了0000的情况！无法计算。

　　β=π/2β=π/2时，sinβ2=cosβ2=0.707sin⁡β2=cos⁡β2=0.707，将其带入公式中有

q=⎡⎣⎢⎢⎢wxyz⎤⎦⎥⎥⎥⎡⎣⎢⎢⎢⎢⎢⎢0.707(cosα2cosγ2+sinα2sinγ2)0.707(sinα2cosγ2−cosα2sinγ2)0.707(cosα2cosγ2+sinα2sinγ2)0.707(cosα2sinγ2−sinα2cosγ2)⎤⎦⎥⎥⎥⎥⎥⎥=⎡⎣⎢⎢⎢⎢⎢⎢0.707cosα−γ20.707sinα−γ20.707cosα−γ20.707sinα−γ2⎤⎦⎥⎥⎥⎥⎥⎥q=[wxyz][0.707(cos⁡α2cos⁡γ2+sin⁡α2sin⁡γ2)0.707(sin⁡α2cos⁡γ2−cos⁡α2sin⁡γ2)0.707(cos⁡α2cos⁡γ2+sin⁡α2sin⁡γ2)0.707(cos⁡α2sin⁡γ2−sin⁡α2cos⁡γ2)]=[0.707cos⁡α−γ20.707sin⁡α−γ20.707cos⁡α−γ20.707sin⁡α−γ2]

　　则xw=zy=tanα−γ2xw=zy=tan⁡α−γ2，于是有

α−γ=2⋅atan2(x,w)α−γ=2⋅atan2(x,w)

 　　通常令α=0α=0，这时γ=−2⋅atan2(x,w)γ=−2⋅atan2(x,w)。可以进行验证：当四元数为(w,x,y,z)=(0.653,-0.271,0.653,0.271)时，根据这些规则计算出来的ZYX欧拉角为α=0°，β=90°，γ=45°

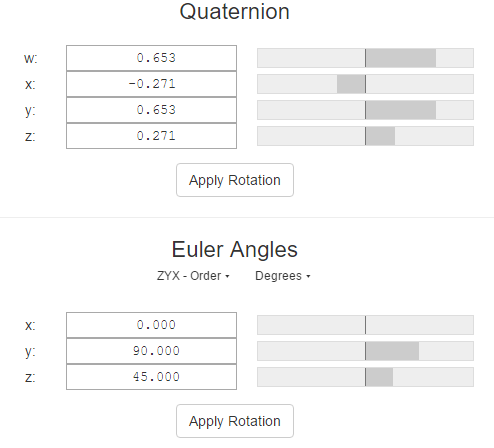
　　当俯仰角为-90°，即机头竖直向下时的情况也与之类似，可以推导出奇异姿态时的计算公式。比较完整的四元数转欧拉角（Z-Y-X order）的代码如下：

复制代码
复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
CameraSpacePoint QuaternionToEuler(Vector4 q) // Z-Y-X Euler angles
{
    CameraSpacePoint euler = { 0 };
    const double Epsilon = 0.0009765625f;
    const double Threshold = 0.5f - Epsilon;

    double TEST = q.w*q.y - q.x*q.z;

    if (TEST < -Threshold || TEST > Threshold) // 奇异姿态,俯仰角为±90°
    {
        int sign = Sign(TEST);

        euler.Z = -2 * sign * (double)atan2(q.x, q.w); // yaw

        euler.Y = sign * (PI / 2.0); // pitch

        euler.X = 0; // roll

    }
    else
    {
        euler.X = atan2(2 * (q.y*q.z + q.w*q.x), q.w*q.w - q.x*q.x - q.y*q.y + q.z*q.z);
        euler.Y = asin(-2 * (q.x*q.z - q.w*q.y));
        euler.Z = atan2(2 * (q.x*q.y + q.w*q.z), q.w*q.w + q.x*q.x - q.y*q.y - q.z*q.z);
    }
        
    return euler;
}
复制代码

 

　　在DirectXMath Library中有许多与刚体姿态变换相关的函数可以直接调用：

  • 四元数乘法：XMQuaternionMultiply method --Computes the product of two quaternions.
  • 旋转矩阵转四元数：XMQuaternionRotationMatrix method --Computes a rotation quaternion from a rotation matrix.
  • 四元数转旋转矩阵：XMMatrixRotationQuaternion method -- Builds a rotation matrix from a quaternion.
  • 欧拉角转四元数：XMQuaternionRotationRollPitchYaw method --Computes a rotation quaternion based on the pitch, yaw, and roll (Euler angles).
  • 四元数转Axis-Angle：XMQuaternionToAxisAngle method --Computes an axis and angle of rotation about that axis for a given quaternion.
  • 欧拉角转旋转矩阵：XMMatrixRotationRollPitchYaw method --Builds a rotation matrix based on a given pitch, yaw, and roll (Euler angles).
  • Axis-Angle转旋转矩阵：XMMatrixRotationAxis method --Builds a matrix that rotates around an arbitrary axis.
  • 构造绕X/Y/Z轴的旋转矩阵：XMMatrixRotationX method --Builds a matrix that rotates around the x-axis.(Angles are measured clockwise when looking along the rotation axis toward the origin)

 　　下面的代码中坐标系绕X轴旋转90°（注意这里不是按照右手定则的方向，而是沿着坐标轴向原点看过去以顺时针方式旋转，因此与传统的右手定则刚好方向相反），来进行变换：

复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
#include "stdafx.h"
#include<iostream>

#include <DirectXMath.h>
using namespace DirectX;

#define PI 3.1415926

int _tmain(int argc, _TCHAR* argv[])
{
    //-------------------Computes the product of two quaternions.
    XMVECTOR q1 = XMVectorSet(1, 1, 3, 2);
    XMVECTOR q2 = XMVectorSet(1, 1, 0, 2);
    XMVECTOR q3 = XMVectorSet(1, 1, 1, 1);

    XMVECTOR result = XMQuaternionMultiply(XMQuaternionMultiply(q3, q2), q1);   // Returns the product of two quaternions as q1*q2*q3

    std::cout << "Quaternion Multiply:" << std::endl;
    std::cout << XMVectorGetX(result) << "," << XMVectorGetY(result) << "," << XMVectorGetZ(result) << "," << XMVectorGetW(result) << std::endl << std::endl;



    //------------------Computes a rotation quaternion based on the pitch, yaw, and roll (Euler angles).
    float pitch = 90.0 * PI / 180.0; // Angle of rotation around the x-axis, in radians.
    float yaw = 0;                     // Angle of rotation around the y-axis, in radians.
    float roll = 0;                     // Angle of rotation around the z - axis, in radians.

    result = XMQuaternionRotationRollPitchYaw(pitch, yaw, roll);

    std::cout << "RPY/Euler angles to Quaternion:" << std::endl;
    std::cout << XMVectorGetX(result) << "," << XMVectorGetY(result) << "," << XMVectorGetZ(result) << "," << XMVectorGetW(result) << std::endl << std::endl;



    //-----------------Computes a rotation quaternion from a rotation matrix.
    float matrix[16] = { 1, 0, 0, 0,   0, 0, 1, 0,   0, -1, 0, 0,   0, 0, 0, 1 };
    XMMATRIX trans(matrix); // Initializes a new instance of the XMMATRIX structure from a sixteen element float array.

    result = XMQuaternionRotationMatrix(trans); // This function only uses the upper 3x3 portion of the XMMATRIX.

    std::cout << "Matrix to Quaternion:" << std::endl;
    std::cout << XMVectorGetX(result) << "," << XMVectorGetY(result) << "," << XMVectorGetZ(result) << "," << XMVectorGetW(result) << std::endl << std::endl;



    //-----------------Builds a rotation matrix from a quaternion.
    trans = XMMatrixRotationQuaternion(result);

    XMFLOAT3X3 fView;
    XMStoreFloat3x3(&fView, trans); // Stores an XMMATRIX in an XMFLOAT3X3
    std::cout << "Quaternion to Matrix:" << std::endl;
    std::cout << fView._11 << "," << fView._12 << "," << fView._13 << std::endl
        << fView._21 << "," << fView._22 << "," << fView._23 << std::endl
        << fView._31 << "," << fView._32 << "," << fView._33 << std::endl << std::endl;



    //-----------------Computes an axis and angle of rotation about that axis for a given quaternion.
    float Angle = 0;
    XMVECTOR Axis;

    XMQuaternionToAxisAngle(&Axis, &Angle, result);

    Axis = XMVector3Normalize(Axis); // Returns the normalized version of a 3D vector
    std::cout << "Quaternion to Axis-Angle:" << std::endl;
    std::cout << "Axis: " << XMVectorGetX(Axis) << "," << XMVectorGetY(Axis) << "," << XMVectorGetZ(Axis) << std::endl;
    std::cout << "Angle: " << Angle*180.0 / PI << std::endl << std::endl;



    //-----------------Builds a matrix that rotates around an arbitrary axis.
    Angle = 90.0 * PI / 180.0;

    trans = XMMatrixRotationAxis(Axis, Angle);

    XMStoreFloat3x3(&fView, trans); // Stores an XMMATRIX in an XMFLOAT3X3
    std::cout << "Axis-Angle to Matrix:" << std::endl;
    std::cout << fView._11 << "," << fView._12 << "," << fView._13 << std::endl
              << fView._21 << "," << fView._22 << "," << fView._23 << std::endl
              << fView._31 << "," << fView._32 << "," << fView._33 << std::endl << std::endl;



    //-----------------Builds a rotation matrix based on a given pitch, yaw, and roll(Euler angles).
    trans = XMMatrixRotationRollPitchYaw(pitch, yaw, roll);

    XMStoreFloat3x3(&fView, trans); // Stores an XMMATRIX in an XMFLOAT3X3
    std::cout << "RPY/Euler angles to Matrix:" << std::endl;
    std::cout << fView._11 << "," << fView._12 << "," << fView._13 << std::endl
        << fView._21 << "," << fView._22 << "," << fView._23 << std::endl
        << fView._31 << "," << fView._32 << "," << fView._33 << std::endl << std::endl;


    //-----------------Builds a matrix that rotates around the x - axis.
    trans = XMMatrixRotationX(Angle); // Angles are measured clockwise when looking along the rotation axis toward the origin.

    XMStoreFloat3x3(&fView, trans); // Stores an XMMATRIX in an XMFLOAT3X3
    std::cout << "Builds a matrix that rotates around the x-axis.:" << std::endl;
    std::cout << fView._11 << "," << fView._12 << "," << fView._13 << std::endl
        << fView._21 << "," << fView._22 << "," << fView._23 << std::endl
        << fView._31 << "," << fView._32 << "," << fView._33 << std::endl << std::endl;

    return 0;
}
View Code

　　结果如下图所示:

 

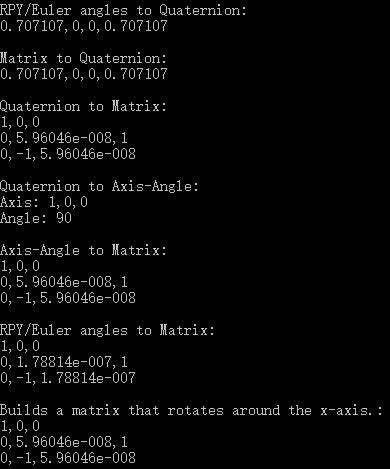
参考：

quaternions.online

DirectXMath Library Quaternion Functions

Convert quaternion to euler rotations

Conversion between quaternions and Euler angles

Maths - Conversion Quaternion to Euler

Coordinate Transformations in Robotics—MATLAB


最后

以上就是凶狠雪糕最近收集整理的关于四元素与欧拉角的全部内容，更多相关四元素与欧拉角内容请搜索靠谱客的其他文章。

本图文内容来源于网友提供，作为学习参考使用，或来自网络收集整理，版权属于原作者所有。
点赞(62)

相关文章

MPU6050欧拉角阐明
MPU6050欧拉角阐明
欧拉角死锁_做控制要知道的刚体旋转知识（三）欧拉角
欧拉角死锁_做控制要知道的刚体旋转知识（三）欧拉角
三维数学--欧拉角与四元数
三维数学--欧拉角与四元数
【unity基础_Day04】 四元数、欧拉角、物理系统
【unity基础_Day04】 四元数、欧拉角、物理系统
四元素与欧拉角
四元素与欧拉角
自动控制（二）
自动控制（二）
unity中的欧拉角
unity中的欧拉角
四元数的理解
四元数的理解

评论列表共有 0 条评论

立即
投稿
返回
顶部