VINS 优化
@(VINS)[VINS]
文章目录
- VINS 优化
- IMU优化
- 特征点重投影优化
- 边缘化优化
- 回环检测优化
- 优化后位姿的更新
IMU优化
已知条件:
(
1
)
{
R
w
b
k
p
b
k
+
1
w
=
R
w
b
k
(
p
b
k
w
+
v
b
k
w
Δ
t
k
−
1
2
g
w
Δ
t
k
2
)
+
α
b
k
+
1
b
k
R
w
b
k
v
b
k
+
1
w
=
R
w
b
k
(
v
b
k
w
−
g
w
Δ
t
k
)
+
β
b
k
+
1
b
k
q
w
b
k
⊗
q
b
k
+
1
w
=
γ
b
k
+
1
b
k
begin{cases} R_w^{b_k} p_{b_{k+1}}^w = R_w^{b_k} left(p_{b_k}^w + v_{b_k}^w {Delta t}_k - frac{1}{2}g^w {Delta t}_k^2right) + {alpha}_{b_{k+1}}^{b_k} \ R_w^{b_k} v_{b_{k+1}}^w = R_w^{b_k} left(v_{b_k}^w - g^w {Delta t}_kright) + {beta}_{b_{k+1}}^{b_k} \ q_w^{b_k} otimes q_{b_{k+1}}^w = {gamma}_{b_{k+1}}^{b_k} end{cases} tag{$1$}
⎩⎪⎨⎪⎧Rwbkpbk+1w=Rwbk(pbkw+vbkwΔtk−21gwΔtk2)+αbk+1bkRwbkvbk+1w=Rwbk(vbkw−gwΔtk)+βbk+1bkqwbk⊗qbk+1w=γbk+1bk(1)
以及雅各比矩阵和协方差矩阵:(具体计算见 “VINS 预积分 雅各比矩阵和协方差矩阵推导过程”)
{
J
k
=
[
J
α
J
β
J
γ
J
b
a
J
b
g
]
=
[
I
f
01
δ
t
−
1
4
(
q
k
+
q
k
+
1
)
δ
t
2
f
04
0
I
−
[
ω
k
+
1
+
ω
k
2
−
b
w
k
]
×
δ
t
0
0
−
δ
t
0
f
21
I
−
1
2
(
q
k
+
q
k
+
1
)
δ
t
f
24
0
0
0
I
0
0
0
0
0
I
]
P
b
k
begin{cases} J_{k} = begin{bmatrix} J^{alpha} \ J^{beta} \ J^{gamma} \ J^{b_a} \ J^{b_g} end{bmatrix} = begin{bmatrix} I & f_{01} & delta t & -frac{1}{4}left(q_k + q_{k+1}right){delta t}^2 & f_{04} \ 0 & I - left[frac{omega_{k+1} + omega_k}{2} - b_{w_k}right]_{times}delta t & 0 & 0 & -delta t \ 0 & f_{21} & I & -frac{1}{2}left(q_k + q_{k+1}right)delta t & f_{24} \ 0 & 0 & 0 & I & 0 \ 0 & 0 & 0 & 0 & I end{bmatrix} \ P_{b_k} end{cases}
⎩⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎧Jk=⎣⎢⎢⎢⎢⎡JαJβJγJbaJbg⎦⎥⎥⎥⎥⎤=⎣⎢⎢⎢⎢⎡I0000f01I−[2ωk+1+ωk−bwk]×δtf2100δt0I00−41(qk+qk+1)δt20−21(qk+qk+1)δtI0f04−δtf240I⎦⎥⎥⎥⎥⎤Pbk
关于偏差一阶近似可以写成:
(
2
)
{
α
b
k
+
1
b
k
≈
α
^
b
k
+
1
b
k
+
J
b
a
α
δ
b
a
k
+
J
b
ω
α
δ
b
ω
k
β
b
k
+
1
b
k
≈
β
^
b
k
+
1
b
k
+
J
b
a
β
δ
b
a
k
+
J
b
ω
β
δ
b
ω
k
γ
b
k
+
1
b
k
≈
γ
^
b
k
+
1
b
k
⊗
[
1
1
2
J
b
ω
γ
δ
b
ω
k
]
begin{cases} {alpha}_{b_{k+1}}^{b_k} approx {hat{alpha}}_{b_{k+1}}^{b_k} + J_{b_a}^{alpha} delta b_{a_k} + J_{b_{omega}}^{alpha} delta b_{{omega}_k} \ {beta}_{b_{k+1}}^{b_k} approx {hat{beta}}_{b_{k+1}}^{b_k} + J_{b_a}^{beta} delta b_{a_k} + J_{b_{omega}}^{beta} delta b_{{omega}_k} \ {gamma}_{b_{k+1}}^{b_k} approx {hat{gamma}}_{b_{k+1}}^{b_k} otimes begin{bmatrix} 1 \ frac{1}{2}J_{b_{omega}}^{gamma} delta b_{{omega}_k} end{bmatrix} end{cases} tag{$2$}
⎩⎪⎪⎪⎨⎪⎪⎪⎧αbk+1bk≈α^bk+1bk+Jbaαδbak+Jbωαδbωkβbk+1bk≈β^bk+1bk+Jbaβδbak+Jbωβδbωkγbk+1bk≈γ^bk+1bk⊗[121Jbωγδbωk](2)
根据
(
1
)
left(1right)
(1) 式我们同样可以得到
α
b
k
+
1
b
k
,
β
b
k
+
1
b
k
,
γ
b
k
+
1
b
k
{alpha}_{b_{k+1}}^{b_k}, {beta}_{b_{k+1}}^{b_k}, {gamma}_{b_{k+1}}^{b_k}
αbk+1bk, βbk+1bk, γbk+1bk
(
3
)
{
α
b
k
+
1
b
k
=
R
w
b
k
(
p
b
k
+
1
w
−
p
b
k
w
+
1
2
g
w
Δ
t
k
2
−
v
b
k
w
Δ
t
k
)
β
b
k
+
1
b
k
=
R
w
b
k
(
v
b
k
+
1
w
+
g
w
Δ
t
k
−
v
b
k
w
)
γ
b
k
+
1
b
k
=
q
b
k
w
−
1
⊗
q
b
k
+
1
w
begin{cases} {alpha}_{b_{k+1}}^{b_k} = R_{w}^{b_k}left(p_{b_{k+1}}^w - p_{b_k}^w + frac{1}{2}g^w{{Delta t}_k}^2 - v_{b_k}^w {Delta t}_kright) \ {beta}_{b_{k+1}}^{b_k} = R_w^{b_k}left(v_{b_{k+1}}^w + g^w Delta t_k - v_{b_k}^wright) \ {gamma}_{b_{k+1}}^{b_k} = {q_{b_k}^w}^{-1} otimes q_{b_{k+1}}^w end{cases} tag{$3$}
⎩⎪⎪⎨⎪⎪⎧αbk+1bk=Rwbk(pbk+1w−pbkw+21gwΔtk2−vbkwΔtk)βbk+1bk=Rwbk(vbk+1w+gwΔtk−vbkw)γbk+1bk=qbkw−1⊗qbk+1w(3)
通过
(
3
)
−
(
2
)
left(3right) - left(2right)
(3)−(2) 式计算残差:
r
e
s
i
d
u
a
l
15
×
1
=
[
δ
α
b
k
+
1
b
k
δ
θ
b
k
+
1
b
k
δ
β
b
k
+
1
b
k
δ
b
a
δ
b
g
]
=
[
R
w
b
k
(
p
b
k
+
1
w
−
p
b
k
w
+
1
2
g
w
Δ
t
k
2
−
v
b
k
w
Δ
t
k
)
−
(
α
^
b
k
+
1
b
k
+
J
b
a
α
δ
b
a
k
+
J
b
ω
α
δ
b
ω
k
)
2
[
(
γ
^
b
k
+
1
b
k
⊗
[
1
1
2
J
b
ω
γ
δ
b
ω
k
]
)
−
1
⊗
(
q
b
k
w
−
1
⊗
q
b
k
+
1
w
)
]
x
y
z
R
w
b
k
(
v
b
k
+
1
w
+
g
w
Δ
t
k
−
v
b
k
w
)
−
(
β
^
b
k
+
1
b
k
+
J
b
a
β
δ
b
a
k
+
J
b
ω
β
δ
b
ω
k
)
b
a
b
k
+
1
−
b
a
b
k
b
ω
b
k
+
1
−
b
ω
b
k
]
residual_{15 times 1} = begin{bmatrix} {delta {alpha}}_{b_{k+1}}^{b_k} \ {delta {theta}}_{b_{k+1}}^{b_k} \ {delta {beta}}_{b_{k+1}}^{b_k} \ delta b_a \ delta b_g end{bmatrix} = begin{bmatrix} R_{w}^{b_k}left(p_{b_{k+1}}^w - p_{b_k}^w + frac{1}{2}g^w{{Delta t}_k}^2 - v_{b_k}^w {Delta t}_kright) - left({hat{alpha}}_{b_{k+1}}^{b_k} + J_{b_a}^{alpha} delta b_{a_k} + J_{b_{omega}}^{alpha} delta b_{{omega}_k}right)\ 2 begin{bmatrix} left({hat{gamma}}_{b_{k+1}}^{b_k} otimes begin{bmatrix} 1 \ frac{1}{2}J_{b_{omega}}^{gamma} delta b_{{omega}_k} end{bmatrix}right)^{-1} otimes left({q_{b_k}^w}^{-1} otimes q_{b_{k+1}}^w right) end{bmatrix}_{xyz} \ R_w^{b_k}left(v_{b_{k+1}}^w + g^w Delta t_k - v_{b_k}^wright) - left({hat{beta}}_{b_{k+1}}^{b_k} + J_{b_a}^{beta} delta b_{a_k} + J_{b_{omega}}^{beta} delta b_{{omega}_k}right)\ {b_a}_{b_{k+1}} - {b_a}_{b_k} \ {b_{omega}}_{b_{k+1}} - {b_{omega}}_{b_k} end{bmatrix}
residual15×1=⎣⎢⎢⎢⎢⎢⎡δαbk+1bkδθbk+1bkδβbk+1bkδbaδbg⎦⎥⎥⎥⎥⎥⎤=⎣⎢⎢⎢⎢⎢⎢⎢⎢⎡Rwbk(pbk+1w−pbkw+21gwΔtk2−vbkwΔtk)−(α^bk+1bk+Jbaαδbak+Jbωαδbωk)2 [(γ^bk+1bk⊗[121Jbωγδbωk])−1⊗(qbkw−1⊗qbk+1w)]xyzRwbk(vbk+1w+gwΔtk−vbkw)−(β^bk+1bk+Jbaβδbak+Jbωβδbωk)babk+1−babkbωbk+1−bωbk⎦⎥⎥⎥⎥⎥⎥⎥⎥⎤
根据
r
e
s
i
d
u
a
l
residual
residual 公式计算对应的雅各比矩阵
注:
R
˙
=
ϕ
∧
R
,
[
q
]
L
=
q
w
I
+
[
0
−
q
v
T
q
v
[
q
v
]
×
]
,
[
q
]
R
=
q
w
I
+
[
0
−
q
v
T
q
v
−
[
q
v
]
×
]
dot{R}=phi^{wedge}R, left[qright]_L = q_w I + begin{bmatrix} 0 & -{q_v}^T \ q_v & left[q_vright]_{times} end{bmatrix}, left[qright]_R = q_w I + begin{bmatrix} 0 & -{q_v}^T \ q_v & -left[q_vright]_{times} end{bmatrix}
R˙=ϕ∧R, [q]L=qwI+[0qv−qvT[qv]×], [q]R=qwI+[0qv−qvT−[qv]×]
- 求第
i
i
i 帧
(
j
=
i
+
1
)
(j = i + 1)
(j=i+1) 的位姿的雅各比矩阵
J p o s e i = [ − R i − 1 [ R i − 1 ∗ ( 0.5 G Δ t 2 + P j − P i − V i Δ t ) ] × 0 3 × 1 0 3 × 3 [ − [ Q j − 1 Q i ] L [ δ q ] R ] b r 3 × 3 0 3 × 1 0 3 × 3 [ Q i − 1 ( G Δ t + V j − V i ) ] × 0 3 × 1 0 3 × 3 0 3 × 3 0 3 × 1 0 3 × 3 0 3 × 3 0 3 × 1 ] J_{pose_i} = begin{bmatrix} -{R_i}^{-1} & left[R_i^{-1} * left(0.5G {Delta t}^2 + P_j - P_i - V_i Delta tright)right]_{times} & 0_{3 times 1} \ 0_{3 times 3} & left[-left[{Q_j}^{-1} Q_iright]_L left[delta qright]_Rright]_{{br}_{3 times 3}} & 0_{3 times 1} \ 0_{3 times 3} & left[{Q_i}^{-1} left(G Delta t + V_j - V_iright)right]_{times} & 0_{3 times 1} \ 0_{3 times 3} & 0_{3 times 3} & 0_{3 times 1} \ 0_{3 times 3} & 0_{3 times 3} & 0_{3 times 1} end{bmatrix} Jposei=⎣⎢⎢⎢⎢⎢⎡−Ri−103×303×303×303×3[Ri−1∗(0.5GΔt2+Pj−Pi−ViΔt)]×[−[Qj−1Qi]L[δq]R]br3×3[Qi−1(GΔt+Vj−Vi)]×03×303×303×103×103×103×103×1⎦⎥⎥⎥⎥⎥⎤
其中:
δ b ω = B ω i − B ω j delta b_{omega} = B_{omega_i} - B_{omega_j} δbω=Bωi−Bωj
δ q = γ ^ j i 1 2 J b ω γ δ b ω delta q = hat{gamma}_j^ifrac{1}{2}J_{b_{omega}}^{gamma} delta b_{omega} δq=γ^ji21Jbωγδbω - 求第
i
i
i 帧
(
j
=
i
+
1
)
(j = i + 1)
(j=i+1) 的
v
b
a
b
ω
v b_{a} b_{omega}
v ba bω 的雅各比矩阵
J s p e e d i = [ − R i − 1 Δ t − J b a α − J b ω α 0 0 [ − [ Q j − 1 Q i δ q ] L ] b r 3 × 3 J b ω α R i − 1 − J b a β − J b ω β 0 − I 0 0 0 − I ] J_{speed_i} = begin{bmatrix} -{R_i}^{-1} Delta t & -J_{b_a}^{alpha} & -J_{b_{omega}}^{alpha} \ 0 & 0 & left[-left[{Q_j}^{-1}Q_i delta qright]_Lright]_{br_{3 times 3}}J_{b_{omega}}^{alpha} \ R_i^{-1} & -J_{b_a}^{beta} & -J_{b_{omega}}^{beta} \ 0 & -I & 0 \ 0 & 0 & -I end{bmatrix} Jspeedi=⎣⎢⎢⎢⎢⎢⎡−Ri−1Δt0Ri−100−Jbaα0−Jbaβ−I0−Jbωα[−[Qj−1Qi δq]L]br3×3Jbωα−Jbωβ0−I⎦⎥⎥⎥⎥⎥⎤ - 求第
j
j
j 帧
(
j
=
i
+
1
)
(j = i + 1)
(j=i+1) 的位姿的雅各比矩阵
J p o s e j = [ R i − 1 0 3 × 3 0 3 × 1 0 3 × 3 [ [ δ q − 1 Q i − 1 Q j ] L ] b r 3 × 3 0 3 × 1 0 3 × 3 0 3 × 3 0 3 × 1 0 3 × 3 0 3 × 3 0 3 × 1 0 3 × 3 0 3 × 3 0 3 × 1 ] J_{pose_j} = begin{bmatrix} {R_i}^{-1} & 0_{3 times 3} & 0_{3 times 1} \ 0_{3 times 3} & left[left[{delta q}^{-1} {Q_i}^{-1} Q_jright]_Lright]_{br_{3 times 3}} & 0_{3 times 1} \ 0_{3 times 3} & 0_{3 times 3} & 0_{3 times 1} \ 0_{3 times 3} & 0_{3 times 3} & 0_{3 times 1} \ 0_{3 times 3} & 0_{3 times 3} & 0_{3 times 1} end{bmatrix} Jposej=⎣⎢⎢⎢⎢⎡Ri−103×303×303×303×303×3[[δq−1Qi−1Qj]L]br3×303×303×303×303×103×103×103×103×1⎦⎥⎥⎥⎥⎤ - 求第
j
j
j 帧
(
j
=
i
+
1
)
(j = i + 1)
(j=i+1) 的
v
b
a
b
ω
v b_{a} b_{omega}
v ba bω 的雅各比矩阵
J s p e e d j = [ 0 0 0 0 0 0 R i 0 0 0 I 0 0 0 I ] J_{speed_j} = begin{bmatrix} 0 & 0 & 0 \ 0 & 0 & 0 \ R_i & 0 & 0 \ 0 & I & 0 \ 0 & 0 & I end{bmatrix} Jspeedj=⎣⎢⎢⎢⎢⎡00Ri00000I00000I⎦⎥⎥⎥⎥⎤
使用最小二乘并加入残差矩阵,优化:
J T P − 1 J = J T P − 1 r e s i d u a l 15 × 1 J^TP^{-1}J = J^TP^{-1} residual_{15 times 1} JTP−1J=JTP−1 residual15×1
由于ceres库的限制,只能使用 J , r e s i d u a l 15 × 1 J , residual_{15 times 1} J, residual15×1优化,为了能够使用协方差,因此,我们重新定义雅各比矩阵和残差 J ′ r e s i d u a l 15 × 1 ′ J' {residual_{15 times 1}}' J′ residual15×1′
J ′ = P − 1 J , r e s i d u a l 15 × 1 ′ = P − 1 r e s i d u a l 15 × 1 J' = sqrt{P^{-1}} J, {residual_{15 times 1}}' = sqrt{P^{-1}} residual_{15 times 1} J′=P−1J, residual15×1′=P−1 residual15×1
这样就可以通过最小二乘的方式就可以使用残差:
J ′ T J ′ = J T P − 1 J , J ′ T r e s i d u a l 15 × 1 ′ = J T P − 1 r e s i d u a l 15 × 1 J'^T J' = J^T P^{-1} J, J'^T {residual_{15 times 1}}' = J^T P^{-1} residual_{15 times 1} J′TJ′=JTP−1J, J′T residual15×1′=JTP−1 residual15×1
其中:
P − 1 = P j − 1 m a t r i x L T sqrt{P^{-1}} = {{{P_j}^{-1}}_{matrixL}}^T P−1=Pj−1matrixLT通过调用Eigen::LLT函数
特征点重投影优化
已知条件有:
- 匹配点对(有像素坐标作用了相机内参矩阵后的点坐标) ( u , v ) left(u, vright) (u,v)为像素坐标,经过相机内参作用得到坐标 ( u − P X F O C U S , v − P Y F O C U S ) left(frac{u-PX}{FOCUS}, frac{v-PY}{FOCUS}right) (FOCUSu−PX,FOCUSv−PY) (匹配点对不需要优化)
- 两帧的位姿 (重投影误差,需要优化)
- IMU坐标系到相机坐标系的变换矩阵 (此参数固定,不会进行优化)
- 匹配点对的深度信息的倒数(重投影误差,需要优化)
即:
{ p t s i = ( x i , y i , 1 ) , p t s j = ( x j , y j , 1 ) Q i , P i , Q j , P j Q i c , T i c D e p i begin{cases} pts_i = left(x_i, y_i, 1right), pts_j = left(x_j, y_j, 1 right) \ Q_i, P_i, Q_j, P_j \ Q_{ic}, T_{ic} \ Dep_i end{cases} ⎩⎪⎪⎪⎨⎪⎪⎪⎧ptsi=(xi,yi,1), ptsj=(xj,yj,1)Qi,Pi,Qj,PjQic,TicDepi
根据 p t s i , Q i , P i , Q j , P j , D e p i pts_i, Q_i, P_i, Q_j, P_j, Dep_i ptsi, Qi, Pi, Qj, Pj, Depi 求 p t s j ′ {pts_j}' ptsj′
p t s j ′ = Q i c − 1 ( Q j − 1 ( Q i ( Q i c p t s i D e p i + T i c ) + P i − P j ) − T i c ) {pts_j}' ={Q_{ic}}^{-1}left({Q_j}^{-1}left(Q_ileft(Q_{ic}frac{pts_i}{Dep_i} + T_{ic}right)+P_i - P_jright) - T_{ic}right) ptsj′=Qic−1(Qj−1(Qi(QicDepiptsi+Tic)+Pi−Pj)−Tic)
令:
p t s _ c a m e r a i = p t s i D e p i pts_camera_i = frac{pts_i}{Dep_i} pts_camerai=Depiptsi
p t s i m u i = Q i c p t s _ c a m e r a i + T i c ptsimu_i = Q_{ic} pts_camera_i + T_{ic} ptsimui=Qic pts_camerai+Tic
p t s i m u j = Q j − 1 ( Q i p t s i m u i + P i − P j ) ptsimu_j = {Q_j}^{-1}left(Q_i ptsimu_i +P_i - P_jright) ptsimuj=Qj−1(Qi ptsimui+Pi−Pj)
然后把 p t s j ′ {pts_j}' ptsj′ 归一化到 z = 1 z = 1 z=1平面 p t s j ′ = p t s j ′ p t s j ′ . z {pts_j}' = frac{{pts_j}'}{{pts_j}'.z} ptsj′=ptsj′.zptsj′
构建优化方程:
min ∣ ∣ p t s j x y ′ − p t s j x y ∣ ∣ 2 min || {pts_j}'_{xy} - {pts_j}_{xy}||^2 min∣∣ptsjxy′−ptsjxy∣∣2
残差为:
r e s i d u a l 2 × 1 = F O C U S 1.5 I 2 × 2 ∗ ( p t s j x y ′ − p t s j x y ) residual_{2 times 1} = frac{FOCUS}{1.5} I_{2 times 2} * left({pts_j}'_{xy} - {pts_j}_{xy}right) residual2×1=1.5FOCUSI2×2∗(ptsjxy′−ptsjxy)
注: F O C U S 1.5 I 2 × 2 frac{FOCUS}{1.5} I_{2 times 2} 1.5FOCUSI2×2 的作用是把残差转化到像素单位
根据最小二乘优化,需要求取雅各比矩阵:
- 第 i i i 帧位姿的雅各比矩阵
- 第 j j j 帧位姿的雅各比矩阵
- Q i c , T i c Q_{ic}, T_{ic} Qic,Tic 的雅各比矩阵(即使不优化也需要求取)
- 特征点深度信息的雅各比矩阵
先求出
p
t
s
j
′
=
p
t
s
j
′
p
t
s
j
′
.
z
{pts_j}' = frac{{pts_j}'}{{pts_j}'.z}
ptsj′=ptsj′.zptsj′方程关于
p
t
s
j
x
,
p
t
s
j
y
{pts_j}_x, {pts_j}_y
ptsjx, ptsjy的导数:
r
e
d
u
c
e
2
×
3
=
F
O
C
U
S
1.5
I
2
×
2
∗
[
1
p
t
s
j
z
0
−
p
t
s
j
x
p
t
s
j
z
∗
p
t
s
j
z
0
1
p
t
s
j
z
−
p
t
s
j
y
p
t
s
j
z
∗
p
t
s
j
z
]
reduce_{2 times 3} = frac{FOCUS}{1.5} I_{2 times 2} * begin{bmatrix} frac{1}{{pts_j}_z} & 0 & -frac{{pts_j}_x}{{pts_j}_z * {pts_j}_z} \ 0 & frac{1}{{pts_j}_z} & -frac{{pts_j}_y}{{pts_j}_z * {pts_j}_z} end{bmatrix}
reduce2×3=1.5FOCUSI2×2∗[ptsjz100ptsjz1−ptsjz∗ptsjzptsjx−ptsjz∗ptsjzptsjy]
第
i
i
i 帧位姿的雅各比矩阵
j
a
c
o
i
2
×
7
=
[
r
e
d
u
c
e
2
×
3
∗
[
R
i
c
−
1
R
j
−
1
−
R
i
c
−
1
R
j
−
1
R
i
[
p
t
s
i
m
u
i
]
×
]
0
2
×
1
]
{jaco_i}_{2 times 7} = begin{bmatrix} reduce_{2 times 3} * begin{bmatrix} {R_{ic}}^{-1}{R_j}^{-1} & -{R_{ic}}^{-1}{R_j}^{-1}R_ileft[ptsimu_iright]_{times} end{bmatrix} & 0_{2 times 1} end{bmatrix}
jacoi2×7=[reduce2×3∗[Ric−1Rj−1−Ric−1Rj−1Ri[ptsimui]×]02×1]
第
j
j
j 帧位姿的雅各比矩阵
j
a
c
o
j
2
×
7
=
[
r
e
d
u
c
e
2
×
3
∗
[
−
R
i
c
−
1
R
j
−
1
R
i
c
−
1
[
p
t
s
i
m
u
j
]
×
]
0
2
×
1
]
{jaco_j}_{2 times 7} = begin{bmatrix} reduce_{2 times 3} * begin{bmatrix} -{R_{ic}}^{-1}{R_j}^{-1} & {R_{ic}}^{-1}left[ptsimu_jright]_{times} end{bmatrix} & 0_{2 times 1} end{bmatrix}
jacoj2×7=[reduce2×3∗[−Ric−1Rj−1Ric−1[ptsimuj]×]02×1]
Q
i
c
,
T
i
c
Q_{ic}, T_{ic}
Qic,Tic 的雅各比矩阵
令:
t
m
p
r
=
R
i
c
−
1
R
j
−
1
R
i
R
i
c
tmp_r = {R_{ic}}^{-1} {R_j}^{-1}R_i R_{ic}
tmpr=Ric−1Rj−1RiRic
j
a
c
o
i
c
2
×
7
=
[
r
e
d
u
c
e
2
×
3
∗
[
R
i
c
−
1
(
R
j
−
1
R
i
−
I
3
×
3
)
−
t
m
p
r
[
p
t
s
_
c
a
m
e
r
a
i
]
×
+
[
t
m
p
r
∗
p
t
s
_
c
a
m
e
r
a
i
]
×
+
[
R
i
c
−
1
(
R
j
−
1
(
R
i
T
i
c
+
P
i
−
P
j
)
−
T
i
c
)
]
×
]
0
2
×
1
]
{jaco_{ic}}_{2 times 7} = begin{bmatrix} reduce_{2 times 3} * begin{bmatrix} {R_{ic}}^{-1} left({R_j}^{-1} R_i - I_{3 times 3}right) & -tmp_r left[pts_camera_iright]_{times} + left[tmp_r * pts_camera_i right]_{times} + left[R_{ic}^{-1}left(R_j^{-1}left(R_i T_{ic} + P_i - P_j right) - T_{ic}right)right]_{times} end{bmatrix} & 0_{2 times 1} end{bmatrix}
jacoic2×7=[reduce2×3∗[Ric−1(Rj−1Ri−I3×3)−tmpr [pts_camerai]×+[tmpr∗pts_camerai]×+[Ric−1(Rj−1(RiTic+Pi−Pj)−Tic)]×]02×1]
特征点深度信息的雅各比矩阵
j
a
c
o
f
e
a
t
u
r
e
2
×
1
=
−
r
e
d
u
c
e
2
×
3
R
i
c
−
1
R
j
−
1
R
i
R
i
c
p
t
s
i
D
e
p
i
2
{jaco_{feature}}_{2 times 1} = -frac{reduce_{2 times 3} {R_{ic}}^{-1}R_j^{-1}R_iR_{ic} pts_i}{Dep_i^2}
jacofeature2×1=−Depi2reduce2×3Ric−1Rj−1RiRic ptsi
根据以上求得的残差矩阵和雅各比矩阵,就可以通过ceres 库对位姿和特征点信息进行最小二乘的优化,在优化过程中有使用损失函数ceres::CauchyLoss(1.0),该函数的是
ρ
(
x
)
=
{
log
(
x
+
1
)
1
x
+
1
−
1
(
x
+
1
)
2
rholeft(xright) = begin{cases} log left(x + 1right) \ frac{1}{x + 1} \ -frac{1}{left(x + 1right)^2} end{cases}
ρ(x)=⎩⎪⎨⎪⎧log(x+1)x+11−(x+1)21
即,
log
(
x
+
1
)
,
log
(
x
+
1
)
′
,
log
(
x
+
1
)
′
′
logleft(x + 1right), logleft(x + 1right)', logleft(x + 1right)''
log(x+1), log(x+1)′, log(x+1)′′ 原型,一阶导,二阶导。
最终的优化函数为
min
ρ
(
∣
∣
p
t
s
j
x
y
′
−
p
t
s
j
x
y
∣
∣
2
)
min rho left(|| {pts_j}'_{xy} - {pts_j}_{xy}||^2right)
minρ(∣∣ptsjxy′−ptsjxy∣∣2)
边缘化优化
边缘化优化中的重投影优化
相比单纯的重投影优化,添加了系数。
已知重投影优化计算出了
r
e
s
i
d
u
a
l
,
J
residual, J
residual, J 在边缘化优化中的重投影优化中
s
q
_
n
o
r
m
=
∣
∣
p
t
s
j
x
y
′
−
p
t
s
j
x
y
∣
∣
2
2
,
r
e
s
i
d
u
a
l
=
r
e
s
i
d
u
a
l
∗
1
s
q
_
n
o
r
m
+
1
,
J
=
1
s
q
_
n
o
r
m
+
1
∗
J
sq_norm = || {pts_j}'_{xy} - {pts_j}_{xy}||^2_2, residual = residual * frac{1}{sqrt{sq_norm }+ 1}, J = frac{1}{sqrt{sq_norm }+ 1} * J
sq_norm=∣∣ptsjxy′−ptsjxy∣∣22, residual=residual∗sq_norm+11, J=sq_norm+11∗J
此操作主要是为了当重投影误差特别大时,我们认为该点不准确,使其权重减小。能够一定程度上减小错误点对优化的影响。
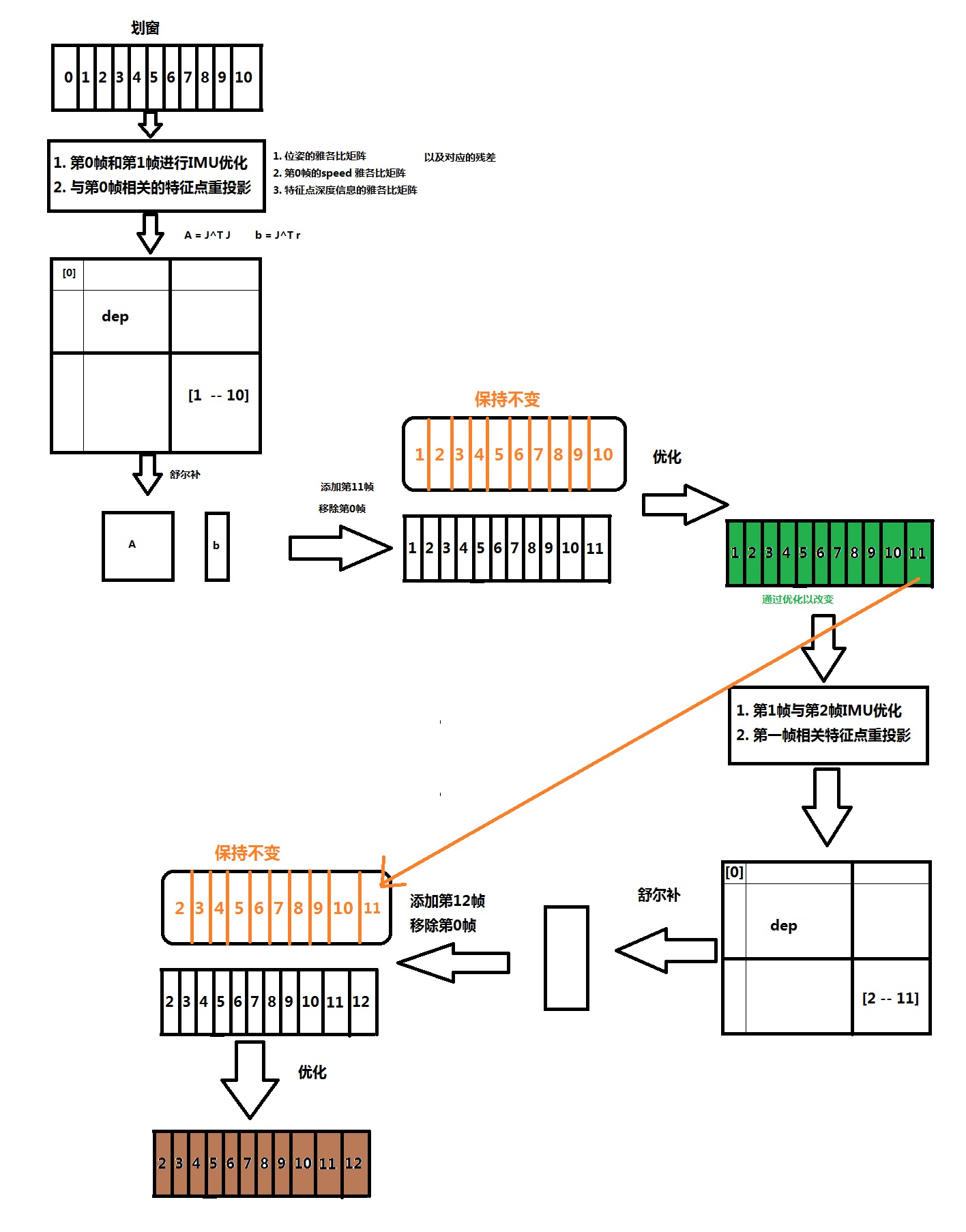
边缘化优化时,添加的优化信息有:
1. 划窗内的第0帧与第1帧之间的IMU优化信息
2. 划窗内与第0帧有关的特征点重投影优化信息
边缘化掉划窗内第0帧相关的信息,需要用到舒尔补,用舒尔补之前我们需要先把包含第0帧相关信息的矩阵构建出来,由于优化使用的最小二乘,因此构建的矩阵如下:
A
=
J
T
J
,
b
=
J
T
r
A = J^T J, b = J^T r
A=JTJ, b=JTr,
r
r
r表示的残差矩阵。
A
X
=
b
AX = b
AX=b
代码如下:
void* ThreadsConstructA(void* threadsstruct)
{
ThreadsStruct* p = ((ThreadsStruct*)threadsstruct);
for (auto it : p->sub_factors)
{
for (int i = 0; i < static_cast<int>(it->parameter_blocks.size()); i++)
{
int idx_i = p->parameter_block_idx[reinterpret_cast<long>(it->parameter_blocks[i])];
int size_i = p->parameter_block_size[reinterpret_cast<long>(it->parameter_blocks[i])];
if (size_i == 7)
size_i = 6;
Eigen::MatrixXd jacobian_i = it->jacobians[i].leftCols(size_i);
for (int j = i; j < static_cast<int>(it->parameter_blocks.size()); j++)
{
int idx_j = p->parameter_block_idx[reinterpret_cast<long>(it->parameter_blocks[j])];
int size_j = p->parameter_block_size[reinterpret_cast<long>(it->parameter_blocks[j])];
if (size_j == 7)
size_j = 6;
Eigen::MatrixXd jacobian_j = it->jacobians[j].leftCols(size_j);
if (i == j)
p->A.block(idx_i, idx_j, size_i, size_j) += jacobian_i.transpose() * jacobian_j;
else
{
p->A.block(idx_i, idx_j, size_i, size_j) += jacobian_i.transpose() * jacobian_j;
p->A.block(idx_j, idx_i, size_j, size_i) = p->A.block(idx_i, idx_j, size_i, size_j).transpose();
}
}
p->b.segment(idx_i, size_i) += jacobian_i.transpose() * it->residuals;
}
}
return threadsstruct;
}
以上信息可以构成一个矩阵,我们分为4部分:
A
A
A矩阵:
A
=
[
A
m
m
A
m
r
A
r
m
A
r
r
]
A = begin{bmatrix} A_{mm} & A_{mr} \ A_{rm} & A_{rr} end{bmatrix}
A=[AmmArmAmrArr]
其中
A
m
m
A_{mm}
Amm中包含 划窗内第0帧位姿,speed 和特征点相关信息。
A
r
r
A_{rr}
Arr中包含划窗内第1帧的speed相关信息和第1帧到第10帧的位姿相关信息,同时包含IMU到Camera坐标系的转换
A
n
g
l
e
i
c
,
T
i
c
Angle_{ic}, T_{ic}
Angleic,Tic信息。
通过舒尔补重新构建矩阵
A
A
A:
A
=
A
r
r
−
A
r
m
∗
A
m
m
i
n
v
∗
A
m
r
A = A_{rr} - A_{rm} * {A_{mm}}_{inv} * A_{mr}
A=Arr−Arm∗Amminv∗Amr
代码:
Eigen::MatrixXd Amm = 0.5 * (A.block(0, 0, m, m) + A.block(0, 0, m, m).transpose());
Eigen::SelfAdjointEigenSolver<Eigen::MatrixXd> saes(Amm);
Eigen::MatrixXd Amm_inv = saes.eigenvectors() * Eigen::VectorXd((saes.eigenvalues().array() > eps).select(saes.eigenvalues().array().inverse(), 0)).asDiagonal() * saes.eigenvectors().transpose();
// 此部分为舒尔补 边缘化优化状态量
Eigen::MatrixXd Amr = A.block(0, m, m, n);
Eigen::MatrixXd Arm = A.block(m, 0, n, m);
Eigen::MatrixXd Arr = A.block(m, m, n, n);
A = Arr - Arm * Amm_inv * Amr;
b
b
b矩阵:
b
=
[
b
m
m
b
r
r
]
b = begin{bmatrix} b_{mm} \ b_{rr} end{bmatrix}
b=[bmmbrr]
通过舒尔补重新构建矩阵
b
b
b:
b
=
b
r
r
−
A
r
m
∗
A
m
m
i
n
v
∗
b
m
m
b=b_{rr} - A_{rm} * {A_{mm}}_{inv} * b_{mm}
b=brr−Arm∗Amminv∗bmm
代码:
Eigen::VectorXd bmm = b.segment(0, m);
Eigen::VectorXd brr = b.segment(m, n);
b = brr - Arm * Amm_inv * bmm;
这样我们就保留了关于第0帧的约束到了通过舒尔补重新构建的矩阵
A
,
b
A, b
A, b 中。
因为现在的矩阵
A
,
b
A, b
A, b 为
A
=
J
T
J
,
b
=
J
T
r
A = J^T J, b = J^T r
A=JTJ, b=JTr 这样的形式,又因为ceres库只能使用最小二乘优化,因此我们需要根据
A
A
A 重新分解出
J
J
J 形式的矩阵。即类似
l
i
n
e
a
r
i
z
e
d
_
j
a
c
o
b
i
a
n
s
=
A
,
,
l
i
n
e
a
r
i
z
e
d
_
r
e
s
i
d
u
a
l
s
=
1
A
b
linearized_jacobians = sqrt{A}, , linearized_residuals = frac{1}{sqrt{A}} b
linearized_jacobians=A,,linearized_residuals=A1b,
l
i
n
e
a
r
i
z
e
d
_
j
a
c
o
b
i
a
n
s
,
l
i
n
e
a
r
i
z
e
d
_
r
e
s
i
d
u
a
l
s
linearized_jacobians, linearized_residuals
linearized_jacobians, linearized_residuals 为优化时使用的矩阵。
现在 l i n e a r i z e d _ j a c o b i a n s , l i n e a r i z e d _ r e s i d u a l s linearized_jacobians, linearized_residuals linearized_jacobians, linearized_residuals 包含的信息为 l i n e a r i z e d _ j a c o b i a n s [ 1 − 10 ] ∣ 0 , l i n e a r i z e d _ r e s i d u a l s [ 1 − 10 ] ∣ 0 linearized_jacobians_{[1-10] | 0}, linearized_residuals_{[1-10] | 0} linearized_jacobians[1−10]∣0,linearized_residuals[1−10]∣0
代码:
Eigen::SelfAdjointEigenSolver<Eigen::MatrixXd> saes2(A);
Eigen::VectorXd S = Eigen::VectorXd((saes2.eigenvalues().array() > eps).select(saes2.eigenvalues().array(), 0));
Eigen::VectorXd S_inv = Eigen::VectorXd((saes2.eigenvalues().array() > eps).select(saes2.eigenvalues().array().inverse(), 0));
Eigen::VectorXd S_sqrt = S.cwiseSqrt();
Eigen::VectorXd S_inv_sqrt = S_inv.cwiseSqrt();
linearized_jacobians = S_sqrt.asDiagonal() * saes2.eigenvectors().transpose();
linearized_residuals = S_inv_sqrt.asDiagonal() * saes2.eigenvectors().transpose() * b;
以上是构建边缘化优化需要的信息。构建完以上信息,划窗内把第0帧信息移除掉,然后进行优化,边缘化优化的信息为:
第1帧到第10帧的位姿。即
P
o
s
e
R
T
[
1
−
10
]
{Pose_{RT}}_{[1-10]}
PoseRT[1−10]
已知条件:
- keep_Pose 第1帧到第10帧的位姿和第1帧的speed (速度v , 陀螺仪偏置bgs , 加速度偏置 bas)信息 。(该信息不进行优化)
- 划窗内的位姿Pose 第1帧到第10帧的位姿和第1帧的speed。(该变量需要进行优化)
优化的方式使用的最小二乘优化,雅各比矩阵和残差矩阵使用 l i n e a r i z e d _ j a c o b i a n s , l i n e a r i z e d _ r e s i d u a l s linearized_jacobians, linearized_residuals linearized_jacobians, linearized_residuals
优化过程中更新雅各比矩阵和残差矩阵的方法为:
δ
x
=
P
o
s
e
−
k
e
e
p
_
P
o
s
e
delta x = Pose - keep_Pose
δx=Pose−keep_Pose
l
i
n
e
a
r
i
z
e
d
_
r
e
s
i
d
u
a
l
s
=
l
i
n
e
a
r
i
z
e
d
_
r
e
s
i
d
u
a
l
s
+
l
i
n
e
a
r
i
z
e
d
_
j
a
c
o
b
i
a
n
s
∗
δ
x
linearized_residuals = linearized_residuals + linearized_jacobians * delta x
linearized_residuals=linearized_residuals+linearized_jacobians∗δx
l
i
n
e
a
r
i
z
e
d
_
j
a
c
o
b
i
a
n
s
=
l
i
n
e
a
r
i
z
e
d
_
j
a
c
o
b
i
a
n
s
linearized_jacobians = linearized_jacobians
linearized_jacobians=linearized_jacobians
代码:
bool MarginalizationFactor::Evaluate(double const *const *parameters, double *residuals, double **jacobians) const
{
int n = marginalization_info->n;
int m = marginalization_info->m;
Eigen::VectorXd dx(n);
for (int i = 0; i < static_cast<int>(marginalization_info->keep_block_size.size()); i++)
{
int size = marginalization_info->keep_block_size[i];
int idx = marginalization_info->keep_block_idx[i] - m;
Eigen::VectorXd x = Eigen::Map<const Eigen::VectorXd>(parameters[i], size);
Eigen::VectorXd x0 = Eigen::Map<const Eigen::VectorXd>(marginalization_info->keep_block_data[i], size);
if (size != 7)
dx.segment(idx, size) = x - x0;
else
{
// delta t
dx.segment<3>(idx + 0) = x.head<3>() - x0.head<3>();
// delta theta
dx.segment<3>(idx + 3) = 2.0 * Utility::positify(Eigen::Quaterniond(x0(6), x0(3), x0(4), x0(5)).inverse() * Eigen::Quaterniond(x(6), x(3), x(4), x(5))).vec();
if (!((Eigen::Quaterniond(x0(6), x0(3), x0(4), x0(5)).inverse() * Eigen::Quaterniond(x(6), x(3), x(4), x(5))).w() >= 0))
{
dx.segment<3>(idx + 3) = 2.0 * -Utility::positify(Eigen::Quaterniond(x0(6), x0(3), x0(4), x0(5)).inverse() * Eigen::Quaterniond(x(6), x(3), x(4), x(5))).vec();
}
}
}
Eigen::Map<Eigen::VectorXd>(residuals, n) = marginalization_info->linearized_residuals + marginalization_info->linearized_jacobians * dx;
if (jacobians)
{
for (int i = 0; i < static_cast<int>(marginalization_info->keep_block_size.size()); i++)
{
if (jacobians[i])
{
int size = marginalization_info->keep_block_size[i], local_size = marginalization_info->localSize(size);
int idx = marginalization_info->keep_block_idx[i] - m;
Eigen::Map<Eigen::Matrix<double, Eigen::Dynamic, Eigen::Dynamic, Eigen::RowMajor>> jacobian(jacobians[i], n, size);
jacobian.setZero();
jacobian.leftCols(local_size) = marginalization_info->linearized_jacobians.middleCols(idx, local_size);
}
}
}
return true;
}
添加新的一帧数据 后,按照同样的方式构建
l
i
n
e
a
r
i
z
e
d
_
j
a
c
o
b
i
a
n
s
,
l
i
n
e
a
r
i
z
e
d
_
r
e
s
i
d
u
a
l
s
linearized_jacobians, linearized_residuals
linearized_jacobians, linearized_residuals
但是keep_Pose有原来的
k
e
e
p
_
P
o
s
e
[
2
−
11
]
=
k
e
e
p
_
P
o
s
e
[
2
−
10
]
+
k
e
e
p
_
P
o
s
e
[
11
]
keep_Pose_{[2-11]} = keep_Pose_{[2-10]} + keep_Pose_{[11]}
keep_Pose[2−11]=keep_Pose[2−10]+keep_Pose[11] 即,前9个位姿使用的还是上一次构建边缘化优化信息,然后再添加新的一帧的位姿。
Pose则是使用的优化过后的划窗内的位姿。
流程如下图:
回环检测优化
-
已经在当前划窗内通过词袋找到与之前关键帧回环的关键帧分别记为cur_KeyFrame, old_KeyFrame。
-
记录相关信息。包括:
- old_KeyFrame的位姿,的关键帧序号
- 匹配点对
- cur_KeyFrame的关键帧序号,时间戳,并标记为回环
-
优化
通过重投影,计算cur_KeyFrame位姿移动到old_KeyFrame位姿的变化量
因为光流跟踪的原因,可以得到划窗内与cur_KeyFrame匹配的点对,然后把cur_KeyFrame位姿当做old_keyFrame位姿,把cur_KeyFrame匹配点的坐标用old_KeyFrame对应点代替,通过重投影计算 Δ R Δ T Delta R Delta T ΔR ΔT,即: w i n d o w _ F r a m e s P o s e , P o i n t s w i n d o w _ F r a m e s , l o o p _ P o s e = c u r _ K e y F r a m e p o s e , P o i n t s o l d _ K e y F r a m e {window_Frames}_{Pose}, Points_{window_Frames}, loop_Pose = {cur_KeyFrame}_{pose}, Points_{old_KeyFrame} window_FramesPose, Pointswindow_Frames, loop_Pose=cur_KeyFramepose, Pointsold_KeyFrame
其中 w i n d o w _ F r a m e s P o s e {window_Frames}_{Pose} window_FramesPose也包含cur帧的位姿,优化的意义不同。 l o o p _ P o s e 、 w i n d o w _ F r a m e s P o s e 、 匹 配 点 的 深 度 信 息 loop_Pose、{window_Frames}_{Pose}、匹配点的深度信息 loop_Pose、window_FramesPose、匹配点的深度信息 为优化对象。
根据优化后的 l o o p _ P o s e ′ {loop_Pose}' loop_Pose′ 和 w i n d o w _ F r a m e s P o s e c u r ′ {{{window_Frames}_{Pose}}_{cur}}' window_FramesPosecur′ 计算出 r e l a t i v e _ t , r e l a t i v e _ q , r e l a t i v e _ y a w relative_t, relative_q, relative_yaw relative_t, relative_q, relative_yaw,此3个参数会用在四自由度的全局优化中。
{ r e l a t i v e _ t = R s _ l o o p − 1 ( P s c u r − P s _ l o o p ) r e l a t i v e _ q = R s _ l o o p − 1 R s c u r r e l a t i v e _ y a w = R s c u r . A n g l e . z − R s _ l o o p . A n g l e . z begin{cases} relative_t = {Rs_loop}^{-1} left(Ps_{cur} - Ps_loop right) \ relative_q = {Rs_loop}^{-1} Rs_{cur} \ relative_yaw = Rs_{cur}.Angle.z - Rs_loop.Angle.z end{cases} ⎩⎪⎨⎪⎧relative_t=Rs_loop−1(Pscur−Ps_loop)relative_q=Rs_loop−1Rscurrelative_yaw=Rscur.Angle.z−Rs_loop.Angle.z
其中 R s _ l o o p P s _ l o o p Rs_loop Ps_loop Rs_loop Ps_loop 由 l o o p _ P o s e ′ {loop_Pose}' loop_Pose′得到
R s c u r P s c u r Rs_{cur} Ps_{cur} Rscur Pscur 由 w i n d o w _ F r a m e s P o s e c u r ′ {{{window_Frames}_{Pose}}_{cur}}' window_FramesPosecur′得到
代码:
for (int i = 0; i< WINDOW_SIZE; i++)
{
if (front_pose.header == Headers[i])
{
Matrix3d Rs_i = Quaterniond(para_Pose[i][6], para_Pose[i][3], para_Pose[i][4], para_Pose[i][5]).normalized().toRotationMatrix();
Vector3d Ps_i = Vector3d(para_Pose[i][0], para_Pose[i][1], para_Pose[i][2]);
Matrix3d Rs_loop = Quaterniond(front_pose.loop_pose[6], front_pose.loop_pose[3], front_pose.loop_pose[4], front_pose.loop_pose[5]).normalized().toRotationMatrix();
Vector3d Ps_loop = Vector3d(front_pose.loop_pose[0], front_pose.loop_pose[1], front_pose.loop_pose[2]);
// relative_t relative_q = delta位姿
// relative_yaw z轴转动的角度
front_pose.relative_t = Rs_loop.transpose() * (Ps_i - Ps_loop);
front_pose.relative_q = Rs_loop.transpose() * Rs_i;
front_pose.relative_yaw = Utility::normalizeAngle(Utility::R2ypr(Rs_i).x() - Utility::R2ypr(Rs_loop).x());
}
}
优化后位姿的更新
- 已知条件
- 优化之前的划窗内的位姿 R s P s S p e e d B i a s Rs Ps SpeedBias Rs Ps SpeedBias
- 优化后的位姿 p a r a _ P o s e Q p a r a _ P o s e T p a r a _ S p e e d B i a s v , b a s , b g s {para_Pose}_Q {para_Pose}_T {para_SpeedBias}_{v, bas, bgs} para_PoseQ para_PoseT para_SpeedBiasv,bas,bgs
- 回环优化后的位姿 R s _ l o o p P s _ l o o p Rs_loop Ps_loop Rs_loop Ps_loop
- 回环old_KeyFrame的位姿 Q o l d P o l d Q_{old} P_{old} Qold Pold
-
以上的四中优化会同时进行,因此会把约束条件罗列到一起,我们知道现在需要优化的变量有:
p a r a _ P o s e Q , p a r a _ P o s e T , p a r a _ S p e e d B i a s , R s _ l o o p , P s _ l o o p , D e p {para_Pose}_Q, {para_Pose}_T, {para_SpeedBias}, Rs_loop, Ps_loop, Dep para_PoseQ, para_PoseT, para_SpeedBias, Rs_loop, Ps_loop, Dep 分别为划窗内的位姿,划窗内的速度、加速度偏置、角速度偏置,回环位姿,特征点深度信息。
优化的内容为:
[ J P o s e [ 0 − 10 ] J S p e e d B i a s [ 0 − 10 ] J D e p [ 0 − 10 ] J M a r g i n a l i z a t i o n [ 1 − 10 ] J L o o p [ 0 − 10 ] ] [ p a r a _ P o s e Q p a r a _ P o s e T p a r a _ S p e e d B i a s R s _ l o o p P s _ l o o p D e p ] = [ r P o s e [ 0 − 10 ] r S p e e d B i a s [ 0 − 10 ] r D e p [ 0 − 10 ] r M a r g i n a l i z a t i o n [ 1 − 10 ] r L o o p [ 0 − 10 ] ] begin{bmatrix} J_{Pose[0 - 10]} \ J_{SpeedBias[0-10]} \ J_{Dep[0 - 10]} \ J_{Marginalization[1 - 10]} \ J_{Loop[0-10]} end{bmatrix} begin{bmatrix} {para_Pose}_Q \ {para_Pose}_T \ {para_SpeedBias} \ Rs_loop \ Ps_loop \ Dep end{bmatrix} = begin{bmatrix} r_{Pose[0 - 10]} \ r_{SpeedBias[0 - 10]} \ r_{Dep[0 - 10]} r_{Marginalization[1 - 10]} \ r_{Loop[0 - 10]} end{bmatrix} ⎣⎢⎢⎢⎢⎡JPose[0−10]JSpeedBias[0−10]JDep[0−10]JMarginalization[1−10]JLoop[0−10]⎦⎥⎥⎥⎥⎤⎣⎢⎢⎢⎢⎢⎢⎡para_PoseQpara_PoseTpara_SpeedBiasRs_loopPs_loopDep⎦⎥⎥⎥⎥⎥⎥⎤=⎣⎢⎢⎡rPose[0−10]rSpeedBias[0−10]rDep[0−10]rMarginalization[1−10]rLoop[0−10]⎦⎥⎥⎤
上式公式,矩阵大小默认自动对齐。这样边缘化优化就会体现出。边缘化优化经过舒尔补的雅各比矩阵就会和其它优化计算出的雅各比矩阵一起约束优化。上式同样是使用最小二乘优化,最终展现是:
∑ J T J X = J T r sum {J^TJ} X = J^T r ∑JTJ X=JTr -
本来优化完的位姿,可以直接使用,考虑到后续的四自由度的全局优化(z轴的转动和位姿),在此我们把z轴的转动消除,消除z轴的转动需要保持消除的值保持一致,因此我们以划窗内的第0帧为标准来消除。
Δ z A n g l e = R s [ 0 ] . A n g l e . z − p a r a _ P o s e Q . A n g l e . z Delta zAngle = Rs_{[0]}.Angle.z - {para_Pose}_Q.Angle.z ΔzAngle=Rs[0].Angle.z−para_PoseQ.Angle.z
计算第0帧z轴的转动量,用3x3矩阵表示:
r o t _ d i f f = ( Δ z A n g l e , 0 , 0 ) . M a t r i x 3 x 3 rot_diff = left(Delta zAngle, 0, 0right).Matrix_{3x3} rot_diff=(ΔzAngle,0,0).Matrix3x3
o r i g i n _ P 0 = P s [ 0 ] origin_P0 = Ps[0] origin_P0=Ps[0]
对优化后的位姿以第0帧为标准消除z轴的转动:
R s = r o t _ d i f f ∗ p a r a _ P o s e R Rs = rot_diff * {para_Pose}_R Rs=rot_diff∗para_PoseR
P s = r o t _ d i f f ∗ ( p a r a _ P o s e T − p a r a _ P o s e [ 0 ] T ) + o r i g i n _ P 0 Ps = rot_diff * left({para_Pose}_T - para_Pose[0]_Tright) + origin_P0 Ps=rot_diff∗(para_PoseT−para_Pose[0]T)+origin_P0
S p e e d B i a s = r o t _ d i f f ∗ p a r a _ S p e e d B i a s SpeedBias = rot_diff * para_SpeedBias SpeedBias=rot_diff∗para_SpeedBias
同理回环也需要如此做:
R s _ l o o p = r o t _ d i f f ∗ R s _ l o o p Rs_loop = rot_diff * Rs_loop Rs_loop=rot_diff∗Rs_loop
P s _ l o o p = r o t _ d i f f ∗ ( P s _ l o o p − p a r a _ P o s e [ 0 ] T ) + o r i g i n _ P 0 Ps_loop = rot_diff * left(Ps_loop - para_Pose[0]_Tright) + origin_P0 Ps_loop=rot_diff∗(Ps_loop−para_Pose[0]T)+origin_P0
现在需要根据回环信息计算优化后的位姿(只是划窗内优化)转到回环 old_KeyFrame 的漂移:
先求z轴的漂移:
d r i f t _ y a w = Q o l d . A n g l e . x − R s _ l o o p . A n g l e . x drift_yaw = Q_{old}.Angle.x - Rs_loop.Angle.x drift_yaw=Qold.Angle.x−Rs_loop.Angle.x
转换为旋转矩阵:
r _ d r i f t = ( d r i f t _ y a w , 0 , 0 ) . M a t r i x 3 x 3 r_drift = left(drift_yaw, 0, 0right).Matrix_{3 x 3} r_drift=(drift_yaw,0,0).Matrix3x3
位移的漂移:
t _ d r i f t = P o l d − r _ d r i f t ∗ P s _ l o o p t_drift = P_{old} - r_drift * Ps_loop t_drift=Pold−r_drift∗Ps_loopr _ d r i f t t _ d r i f t r_drift t_drift r_drift t_drift为漂移量
深度信息直接使用优化后的深度信息。
代码:
void VINS::new2old()
{
Vector3d origin_R0 = Utility::R2ypr(Rs[0]);
Vector3d origin_P0 = Ps[0];
if (failure_occur)
{
origin_R0 = Utility::R2ypr(last_R_old);
origin_P0 = last_P_old;
}
// 优化后的第0帧的相机位姿
Vector3d origin_R00 = Utility::R2ypr(Quaterniond(para_Pose[0][6],
para_Pose[0][3],
para_Pose[0][4],
para_Pose[0][5]).toRotationMatrix());
// z轴转动的角度
double y_diff = origin_R0.x() - origin_R00.x();
//TODO
Matrix3d rot_diff = Utility::ypr2R(Vector3d(y_diff, 0, 0));
for (int i = 0; i <= WINDOW_SIZE; i++)
{
Rs[i] = rot_diff * Quaterniond(para_Pose[i][6], para_Pose[i][3], para_Pose[i][4], para_Pose[i][5]).normalized().toRotationMatrix();
Ps[i] = rot_diff * Vector3d(para_Pose[i][0] - para_Pose[0][0],
para_Pose[i][1] - para_Pose[0][1],
para_Pose[i][2] - para_Pose[0][2]) + origin_P0;
Vs[i] = rot_diff * Vector3d(para_SpeedBias[i][0],
para_SpeedBias[i][1],
para_SpeedBias[i][2]);
Bas[i] = Vector3d(para_SpeedBias[i][3],
para_SpeedBias[i][4],
para_SpeedBias[i][5]);
Bgs[i] = Vector3d(para_SpeedBias[i][6],
para_SpeedBias[i][7],
para_SpeedBias[i][8]);
}
Vector3d cur_P0 = Ps[0];
if (LOOP_CLOSURE && loop_enable)
{
loop_enable = false;
for (int i = 0; i< WINDOW_SIZE; i++)
{
if (front_pose.header == Headers[i])
{
Matrix3d Rs_loop = Quaterniond(front_pose.loop_pose[6], front_pose.loop_pose[3], front_pose.loop_pose[4], front_pose.loop_pose[5]).normalized().toRotationMatrix();
Vector3d Ps_loop = Vector3d(front_pose.loop_pose[0], front_pose.loop_pose[1], front_pose.loop_pose[2]);
Rs_loop = rot_diff * Rs_loop;
Ps_loop = rot_diff * (Ps_loop - Vector3d(para_Pose[0][0], para_Pose[0][1], para_Pose[0][2])) + origin_P0;
double drift_yaw = Utility::R2ypr(front_pose.Q_old.toRotationMatrix()).x() - Utility::R2ypr(Rs_loop).x();
r_drift = Utility::ypr2R(Vector3d(drift_yaw, 0, 0));
//r_drift = front_pose.Q_old.toRotationMatrix() * Rs_loop.transpose();
t_drift = front_pose.P_old - r_drift * Ps_loop;
}
}
}
for (int i = 0; i < NUM_OF_CAM; i++)
{
tic = Vector3d(para_Ex_Pose[i][0],
para_Ex_Pose[i][1],
para_Ex_Pose[i][2]);
ric = Quaterniond(para_Ex_Pose[i][6],
para_Ex_Pose[i][3],
para_Ex_Pose[i][4],
para_Ex_Pose[i][5]).toRotationMatrix();
}
VectorXd dep = f_manager.getDepthVector();
for (int i = 0; i < f_manager.getFeatureCount(); i++)
{
dep(i) = para_Feature[i][0];
}
f_manager.setDepth(dep);
}
##四自由度优化
- 四自由度优化必须在有回环的条件下进行
- 该优化不会使用到特征点信息,只用到关键帧的位姿信息
- 该优化的残差主要是由回环信息计算出
- 该优化使用的关键帧位姿为IMU积分通过划窗优化得到的位姿
- 该优化最终会重新给出一个漂移量 r _ d r i f t t _ d r i f t r_drift t_drift r_drift t_drift
- 该优化只会优化回环内关键帧的位姿
- old_KeyFrame的位姿固定
推理公式
该帧没有回环:
已知关键帧的位姿 R i , T i R_i, T_i Ri, Ti 和与该关键帧相差5帧以内, 并在该关键帧之前 的某一关键帧位姿 R i − j , T i − j R_{i-j}, T_{i - j} Ri−j, Ti−jC o n s A n g l e i − j = A n g l e i − j ConsAngle_{i - j} = Angle_{i - j} ConsAnglei−j=Anglei−j
Δ T = R i − j − 1 ( T i − T i − j ) Delta T = {R_{i - j}}^{-1}left(T_{i} - T_{i-j}right) ΔT=Ri−j−1(Ti−Ti−j)
Δ z A n g l e = A n g l e i . z − A n g l e i − j . z Delta zAngle = Angle_{i}.z - Angle_{i - j}.z ΔzAngle=Anglei.z−Anglei−j.z
优化迭代过程: 默认只有z轴转动
R i − j w = ( A n g l e i − j . z , C o n s A n g l e i − j . y , C o n s A n g l e i − j . z ) R_{i - j}^w = left(Angle_{i - j}.z, ConsAngle_{i - j}.y, ConsAngle_{i - j}.zright) Ri−jw=(Anglei−j.z,ConsAnglei−j.y,ConsAnglei−j.z)
Δ T ′ = R i − j w − 1 ( T i − j − T i ) {Delta T}' = {R_{i - j}^w}^{-1}left(T_{i - j} - T_{i}right) ΔT′=Ri−jw−1(Ti−j−Ti)最终计算出的残差为:
r e s i d u a l s 4 × 1 = [ Δ T ′ − Δ T A n g l e i . z − A n g l e i − j . z − Δ z A n g l e ] residuals_{4 times 1} = begin{bmatrix} {Delta T}' - Delta T \ Angle_{i}.z - Angle_{i - j}.z - Delta zAngle end{bmatrix} residuals4×1=[ΔT′−ΔTAnglei.z−Anglei−j.z−ΔzAngle]
雅各比矩阵使用的自动求导方式获得,ceres有自动求导的函数。
该过程中用到损失函数ceres::HuberLoss(1.0)
ρ ( s ) = { s s < = 1 2 s − 1 s > = 1 rholeft(sright) = begin{cases} s qquad qquad s <= 1 \ 2sqrt{s} - 1 quad s >= 1 end{cases} ρ(s)={ss<=12s−1s>=1
残差经过损失函数作用 r e s i d u a l s 4 × 1 = ρ ( ∥ r e s i d u a l s 4 × 1 ∥ 2 2 ) r e s i d u a l s 4 × 1 residuals_{4 times 1} = rholeft(|residuals_{4 times 1}|_2^2right)residuals_{4 times 1} residuals4×1=ρ(∥residuals4×1∥22)residuals4×1
以上j = {1, 2, 3, 4, 5}
该帧有回环:
已知有 R o l d , T o l d , R i , T i , r e l a t i v e _ t , r e l a t i v e _ q , r e l a t i v e _ y a w R_{old}, T_{old}, R_i, T_i, relative_t, relative_q, relative_yaw Rold, Told, Ri, Ti, relative_t, relative_q, relative_yaw
其中 Δ T = r e l a t i v e _ t , Δ z A n g l e = r e l a t i v e _ y a w Delta T = relative_t, Delta zAngle = relative_yaw ΔT=relative_t, ΔzAngle=relative_yaw
C o n s A n g l e o l d = A n g l e o l d ConsAngle_{old} = Angle_{old} ConsAngleold=Angleold
使用同样的方式计算出残差,不同的是,计算出的残差在位移上的残差添加了一个系数10, 此做法应该是,优化的过程中,我们更应该关注回环的残差。
r e s i d u a l s 4 × 1 = [ ( Δ T ′ − Δ T ) ∗ 10 A n g l e i . z − A n g l e i − j . z − Δ z A n g l e ] residuals_{4 times 1} = begin{bmatrix} left({Delta T}' - Delta Tright) * 10 \ Angle_{i}.z - Angle_{i - j}.z - Delta zAngle end{bmatrix} residuals4×1=[(ΔT′−ΔT)∗10Anglei.z−Anglei−j.z−ΔzAngle]
雅各比矩阵同样使用的ceres的自动求导。
以上优化完之后,需要根据cur_KeyFrame, old_KeyFrame重新跟新漂移量 r _ d r i f t t _ d r i f t r_drift t_drift r_drift t_drift
已知 R c u r , T c u r , O r i g i n R c u r , O r i g i n T c u r R_{cur}, T_{cur}, OriginR_{cur}, OriginT_{cur} Rcur, Tcur, OriginRcur, OriginTcur, 其中 R c u r , T c u r R_{cur}, T_{cur} Rcur, Tcur为优化后的位姿, O r i g i n R c u r , O r i g i n T c u r OriginR_{cur}, OriginT_{cur} OriginRcur, OriginTcur为积分得到并经过划窗优化的位姿
y a w _ d r i f t = A n g l e c u r . z − O r i g i n A n g l e c u r . z yaw_drift = Angle_{cur}.z - OriginAngle_{cur}.z yaw_drift=Anglecur.z−OriginAnglecur.z
r _ d r i f t = ( y a w _ d r i f t , 0 , 0 ) . M a t r i x 3 x 3 r_drift = left(yaw_drift, 0, 0right).Matrix_{3 x 3} r_drift=(yaw_drift,0,0).Matrix3x3
t _ d r i f t = T c u r − r _ d r i f t ∗ O r i g i n T c u r t_drift = T_{cur} - r_drift * OriginT_{cur} t_drift=Tcur−r_drift∗OriginTcur
最后
以上就是心灵美大船最近收集整理的关于VINS 优化VINS 优化的全部内容,更多相关VINS内容请搜索靠谱客的其他文章。








发表评论 取消回复