背包问题终结篇（上）

72 阅读 0 评论 48 点赞

我是靠谱客的博主舒服毛豆，最近开发中收集的这篇文章主要介绍背包问题终结篇（上），觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

背包问题介绍
背包问题是一个非常典型的考察动态规划应用的题目，对其加上不同的限制和条件，可以衍生出诸多变种，若要全面理解动态规划，就必须对背包问题了如指掌。

首先记住解决动态规划的三个基本要素：
最优子结构
边界条件
状态转移方程

1.0-1背包问题
即限定每个物品要么拿（1个）要么不拿（0个）
典型问题描述：

一个小偷面前有一堆（n个）财宝，每个财宝有重量w和价值v两种属性，而他的背包只能携带一定重量的财宝（Capacity），在已知所有财宝的重量和价值的情况下，如何选取财宝，可以最大限度的利用当前的背包容量，取得最大价值的财宝（或求出能够获取财宝价值的最大值）

问题分析：
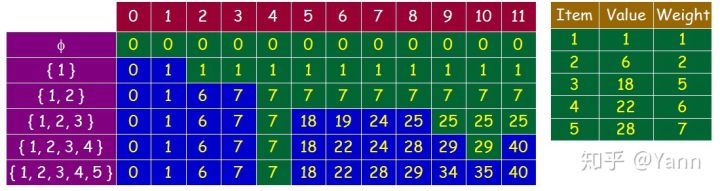
这个问题有两个维度，一个是当前物品i，另一个是当前容量c，于是我们可以用f[n,c]来表示将n个物品放入容量为C的背包可以得到的最大收益，而第i个物品无非拿与不拿两种情况，拿的情况下，f[i][c]=f[i-1][c-w[j]+v[i]],这个公式表示在第i个物品选择拿的情况下，同时还有前i-1的物品的选择的最优子结构，不拿的情况下，f[i][c]=f[i - 1][c],而且要使尽量拿的价值最大。
因此可以表示为：

f[i][c] = max( f[i - 1][c], f[i - 1][c - w[i]] + v[i] )
这便是我们的最优子结构，即不拿第 i 件物品和拿第 i 件物品中的最大值，当然，这里要保证w[i] <= c，否则f[i][c] = f[i - 1][c]。

代码如下：

#include<stdio.h>
int f[100][100];
 int n;
 int Maxweight;
int max(int a,int b)
{
 if(a>b)
 return a;
 else
 return b;
} 
int bag0_1(int v[100],int w[100],int n,int c)
{
 int i,j;
 for(i=0;i<n;i++)
 f[i][0]=0;
 for(j=1;j<=c;j++)
 {
  if(j>=w[0])
  f[0][j]=v[0];
  else
  f[0][j]=0;
  } 
  for(i=1;i<n;i++)
  {
   for(j=1;j<=c;j++)
   {
    if(j<w[i])
    {
     f[i][j]=f[i-1][j];
  }
  else
  {
   f[i][j]=max(f[i-1][j],f[i-1][j-w[i]]+v[i]);
  }
   }
  }
  for(i=0;j<n;i++)
  {
  for(j=0;j<=c;j++)
  printf("%d ",f[i][j]);
  printf("n");
  }
  return f[n-1][c];
}
int main()
{
 int i,j;
 int Maxvalue;
 int value[100];
 int weight[100];
 scanf("%d",&n);
 scanf("%d",&Maxweight);
 for(i=0;i<n;i++)
 scanf("%d",&value[i]);
 for(j=0;j<n;j++)
 scanf("%d",&weight[j]);
 Maxvalue=bag0_1(value,weight,n,Maxweight);
 printf("小偷可以拿走的最大价值为：%d",Maxvalue);
 return 0;
 }

在这里插入图片描述

这样不是最优的解，我们还可以空间优化，使用一维数组解决问题，同时从右往左填表。

int bag0_1(int v[100],int w[100],int n,int c)
{
 int i,j;
     for(int i = 0; i < n; i++){
        for(int j = c; j >= w[i]; j--)
            f[j] = max(f[j], f[j - w[i]] + v[i]);
    }
    return f[c];
}

这样相当于永远只保存一行数据，根据前面数组前面的数据更新后面的，最后就得到了上面图片的最后一行。

题目会要求我们输出最优解，而不只是最优解的答案，这时我们就无法在空间上对算法进行优化了，因为我们需要每一次变化中保存的值，以回溯最优解（以上题的小偷为例子）

 i = n;
 j = Maxweight;
 while(i>0){
    if(f[i][j] == f[i - 1][j])
    printf("未选第 %d 件物品n",i);
    else if(f[i][j] == f[i - 1][j - w[i]] + v[i]) {
    printf("选第 %d 件物品n",i);
        j -= w[i];
    }
    i--;
}

这里是要求背包装有最大价值的物品，没有规定必须将背包装满，如果规定背包必须装满，那么除了f[0]初始化为0，其他的f[1~C]都要初始化为INT_MIN，可以理解为没有物品时，如果背包容量为0，那么什么都不装就是刚好装满，价值为0，而如果背包容量大于0，说明初始情况除了f[0]外我们哪种情况都装不满，因此把那些无解的情况初始化为负无穷。

完全背包问题

如果不限定每种物品的数量，同一样物品想拿多少拿多少，则问题称为无界或完全背包问题。如果一件物品没有件数限制，那么我们可以取0、1、2、…至多可以取C/w[i]件，按照之前的分析，状态转移方程可以改写为f[i][j] = max( f[i - 1][j], f[i - 1][j - k * w[i]] + k * v[i] )其中k需满足0 <= kw[i] <= j，那么此时的时间复杂度就变成了O(nC*Σ(C/w[i]))

代码如下：

int absolute_bag(int v[100],int w[100],int n,int c)
{
 int i,j;
  for(i=1;i<=n;i++)
  {
   for(j=1;j<=c;j++)
   {
    if(j<w[i])
    {
     f[i][j]=f[i-1][j];
  }
  else
  {
   int k;
   int maxV =j/w[i];
                    for(k=0;k<maxV+1;k++){
                        f[i][j]=max(f[i-1][j],f[i-1][j-k*w[i]]+k*v[i]);
             }
  }
   }
  }
  return f[n][c];
}

很明显可以对它进行优化,先回想一下0-1背包问题中的两层循环，第一层为0至n-1，第二层从右至左C至w[i]，而这里从右至左更新的原因，是为了保证第 i 件物品的状态一定由第 i - 1 件物品的状态得来，也就是说，考虑第 i 件物品时，依据的是一个一定没有选中过 i - 1 件物品的结论，因此如果将第二层循环改为从左至右，由w[i]至C，就变成了选第 i 件物品时依然从已经拿过第 i 件物品的结论中递推，此时的状态转移方程可以写为：

f[i][j] = max( f[i - 1][j], f[i][j - w[i]] + v[i] )

注意这里变成了i，我们不再需要k这个变量

于是我们便可以写出优化后解决完全背包问题的代码：

int absolute_bag(int v[100],int w[100],int n,int c)
{
 int i,j;
     for(i = 0; i < n; i++){
        for(j = w[i]; j<=c; j++)
             f[j] = max(f[j-w[i]]+v[i],f[j]);
    }
    return f[c];
}

理解了上面的两个状态转移方程，就可以利用0-1背包问题的解决思路，顺利解决完全背包问题。可以看到这和0-1背包问题的写法几乎一致，不同的只是第二层循环变成了从左至右更新。

多重背包问题

如果限定物品i最多只能拿m[i]个，则问题称为有界或多重背包问题。类似的，此时的状态转移方程可以写为：f[i][j] = max{f[i -
1][j - k * w[i]] + k * v[i] | 0 ≤ k ≤ m[i]}

代码如下：

int double_bag(int v[100],int w[100],int num[100],int n,int c)
{
 int i,j;
  for(i=1;i<=n;i++)
  {
   for(j=1;j<=c;j++)
   {
    if(j<w[i])
    {
     f[i][j]=f[i-1][j];
  }
  else
  {
   int k;
   int maxV =min(num[i],j/w[i]);
                    for(k=0;k<maxV+1;k++){
                        f[i][j]=max(f[i-1][j],f[i-1][j-k*w[i]]+k*v[i]);
             }
  }
   }
  }
  return f[n][c];
}

混合三种背包问题

如果物品中既有最多只能拿m[i]个物品，又有不限数量的物品，又有只有一件的物品，我们该如何选取呢？这个问题看起来非常复杂，但是其实仔细分析一下，我们可以将前面的三种背包问题作为三种不同的情况来将复杂的问题简单化。这里就可以体现出我们前面将三种情况抽象成函数的意义了：

int f[100];
for(int i = 0; i < n; i++){
    if(m[i] == 1)               // 为0-1背包
        bag0_1(v,w,n,c)
    else if(m[i] == INT_MAX)    // 为完全背包
       absolute_bag(v,w,n,c)
    else                        // 为多重背包
        double_bag( v,w,num, n,c)
}