算法之动态规划，问题三：0 1 背包问题

1 问题的描述

0 1 背包的问题：
有n个物品(权重Wi>0，价值Vi>0),一个背包最多装W重量的物品，并且物品只有装/不装两种可能。
目标：怎么装物品，才是使背包的物品价值和最大？
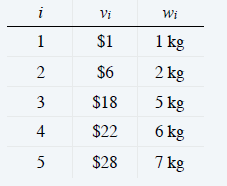
举例：下面是物品的基本信息，背包最多装11kg的物品。

方案一： 1、2、5 的重量和10kg，价值和$35
方案二：3、4 的重量和11kg，价值和$40
明显方案二优于方案一，怎么通过算法实现呢？

2 贪心算法？

其实这个问题很像“带权重的任务安排问题”。请参考https://blog.csdn.net/weixin_39956356/article/details/101623749
（1）：如果是分数背包问题（一个物品可以装一部分），就可以使用贪心算法。选择性价比最大的装就行了。但是这个问题只有装/不装，要使用动态规划来解决。
（2）：对于什么是动态规划，我想再弄出一篇文章。

3 算法的参数约定及递推式

我们定义一个参数：OPT(i,w)
根据问题的不同，优化目标的参数可能会有多个，这里有两个参数：分别是i（当前背包存放物品的数量）、w（当前背包重量）

定义：OPT(i,w)= 装前i个物品重w（1，2，3...i）。
目标：OPT(n,W)，原问题-在县中W的背包中装n个物品。
显然有两种方案，即（1）选择i物品（2）不选择i物品，动态规划**问题分析是自顶而下的思路**，但是算法实现却是自底而上的策略。
case 1:
	如果不选择i物品，原问题蜕化成OPT(i-1，w)，即i物品没装入，能装的重量不变w，看看下一个物品i-1可以装吗？
case 2:
	如果选择i物品，原问题退化成vi+OPT(i-1，w-wi),即既然选择了i物品，能装的重量减少wi,并尝试下一个物品i-1,其中Wi是i物品的权重。
递推如下：

看到这里，如果你之前没有参加过算法课程的话，或许对OPT(i,w)还有些疑惑，里面到底装的什么？为此，结合上面的一个实例化背包，我们看看这个二维数组。
通过分析，可以得到下面的信息
（1）：这个二位数组其实有6行12列，动态分配时因该注意。
（2）：第一行是全0，OPT(0,w)–>没有物品，包的重量为0啊。
（3）：表的计算顺序：从左至右，从上至下。（自底向上）
（4）：这里我分析一个数据的由来，其他的类似。

OPT(4,11)=40,是怎么来的呢？
这个问题其实讨论 装4号物品/不装4号物品，取大者。
case 1 :装4号物品，显然由递推式有，OPT(4,11)=v4+OPT(3,11-w4)=22+OPT(3,5)(查表获得) = 22+18=40。
case 1 :不装4号物品，显然由递推式有，OPT(4,11)= OPT(3,11)=25。
比较可知OPT(4,11)=40，取大者。

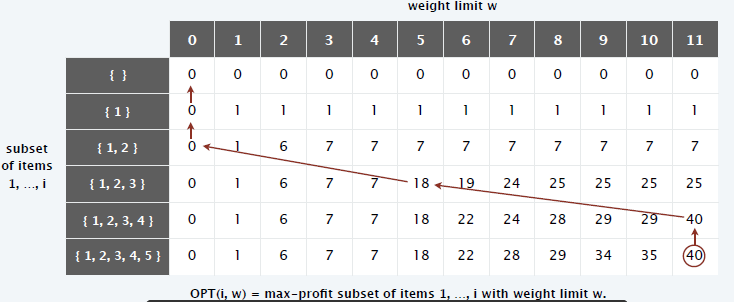
（4）：图中红线是回溯到底背包装了啥物品。

4 算法具体实现

(1)：二维数组m是OPT(i,w)
(2)：i:物品的数量，从1到itemNum
(3)： w:背包的当前重量，最开始没有物品为0，慢慢增加到maxWeight

void DynamicKnapsack(ITEM_INFO *items, int** m, int maxWeight, int itemNum)
{
	//其实首先是将m[0, ],第一行清零，由于之前全清零了，所以就没做这步了

	for (unsigned int i = 1; i <= itemNum; i++)											//i:物品的数量，从1到itemNum
	{
		for (unsigned int w = 0; w <= maxWeight; w++)									//w:背包的当前重量，最开始没有物品为0，慢慢增加到maxWeight
		{
			//分两种情况，(1)i号物品不放入背包；(2 else)i号物品放入背包
			if (items[i-1].wight > w) {
				m[i][w] = m[i-1][w];
			}else{
				//OPT(i,w) <== OPT(i-1, w) ? Vi+OPT(i-1, w-wi)
				if (m[i-1][w] > items[i-1].value + m[i - 1][w - items[i-1].wight])
					m[i][w] = m[i - 1][w];
				else
					m[i][w] = items[i-1].value + m[i - 1][w - items[i-1].wight];
			}
		}
	}
}

对这段代码或许还有一个疑惑？那就是if的判断条件，如下：

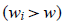
其实很简单，想想？，i个物品重量都大于当前允许的最大值w，还装的下吗？

5 回溯原问题的解

这里和最前面的“带权重的任务安排问题”很类似。
https://blog.csdn.net/weixin_39956356/article/details/101623749
但是，这里任然需要注意的一点：

递归出口是（i == 0 || w == 0）

	if (i == 0 || w == 0)
		return;

因为没有w == 0条件的话，回溯到背包已经不能装物品了的时候w=0，此时i可能还不为0，见上i=2的时候已经为0了哈。再继续递归，会进入if里面，强制执行w - items[i - 1].wight，显然为负数，非法访问内存！！！出错。

int g_i = 0;			//返回活动j存在path中
void FindSolution(ITEM_INFO *items, int** m, int i, int w, int* path)
{
	if (i == 0 || w == 0)
		return;
	else if (m[i - 1][w] < items[i - 1].value + m[i - 1][w - items[i - 1].wight])	//当w=0,不能执行这里了，重量已经0，还减少？越界，所以不加m==0判断，下面执行出错误
	{
		//i物品选中，迭代时候数量i减一，背包能容量的重量减wi
		path[g_i++] = i;
		return FindSolution(items, m, i - 1, w - items[i - 1].wight, path);			//这里是items[i - 1]，因为第一个物品信息存放在0号内存单元的
	}
	else
		//i物品没选中，迭代时候数量i减一即可
		return FindSolution(items, m, i - 1, w, path);
}

6 案例输出

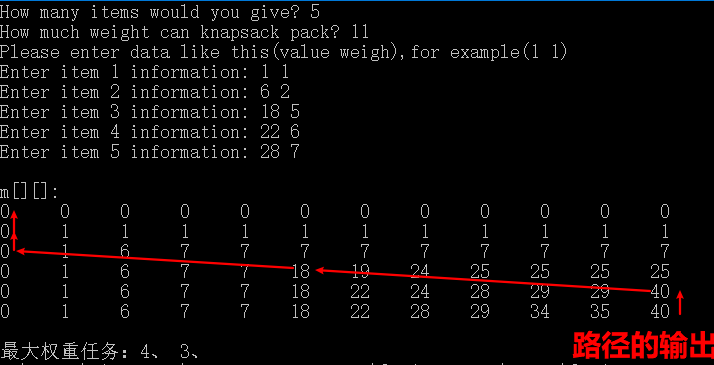
7 源代码

链接: https://pan.baidu.com/s/1CQgvOb-RxQn4CmHtZXOj6g 提取码: untc 失效请留言。

最后

以上就是妩媚雨为你收集整理的算法之动态规划，问题三：0 1 背包问题的全部内容，希望文章能够帮你解决算法之动态规划，问题三：0 1 背包问题所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。