DP + 完全背包问题：PIPI的存钱罐

完全背包问题

  之前我们讲了01背包问题：DP + 01背包问题：饭卡。现在我们来看看完全背包问题，完全背包问题与01背包问题唯一的区别就是：01背包问题中的每个物品都只有一个，只能装一次，而完全背包问题中的每件物品都有无数个，可以装任意次。
  我们还是给出完全背包问题的描述：给定 n 种物品和一个空间为 C 的背包，第i种物品的体积是vi，其价值为wi ，每种物品有无数个。应该如何选择装入背包的物品，在不超过背包容量的前提下，使装入背包中的物品总价值最大？
  在之前的文章中，已经分析过了01背包问题的状态转移方程，这里直接将代码贴出来：

for (int i = 1; i <= n; i++) {
	for (int j = C; j >= vi; j--) {
		dp[j] = Math.max(dp[j], dp[j - vi] + wi);
	}
}

  完全背包问题的状态转移原理与01背包问题是一样的：对于某个背包容量j，其能承载的最大价值，一定是由比它容量少vi的背包装入了体积为vi的物品转移得到。那么我们如何在代码中体现每件物品可以重复装入呢？
  在之前的文章中，我们分析过在01背包问题代码中，j必须从后向前开始遍历，这样才能保证只装一个物品，那么j从前向后遍历，是不是就能将某件物品装入多次呢？事实确实是这样，核心点在于当前状态继承的是已经被更新的状态，还是未被更新的状态。对于j从后向前开始遍历，当前遍历状态继承的是未被更新的状态，其由未被更新的状态转移得到，而未被更新的状态则表示没有将物品装入。对于j从前向后开始遍历，当前遍历状态继承的是已经被更新的状态，其由已经被更新的状态转移得到，而已经被更新的状态则表示已经将物品装入，若发生状态转移，则表明进行了物品的重复装入。
  来举个例子：现在只有1个物品，v=w=1，C=3，dp数组初始值为0。对于j从后向前遍历，计算的过程是：

dp[3] = max(dp[3],dp[2] + 1) = max(0, 0 + 1) = 1 //装入物品1次
dp[2] = max(dp[2],dp[1] + 1) = max(0, 0 + 1) = 1 //装入物品1次
dp[1] = max(dp[1],dp[0] + 1) = max(0, 0 + 1) = 1 //装入物品1次

  上述过程对应的即是01背包的求解过程
  对于j从前向后遍历，计算的过程是：

dp[1] = max(dp[1],dp[0] + 1) = max(0, 0 + 1) = 1 //装入物品1次
dp[2] = max(dp[2],dp[1] + 1) = max(0, 1 + 1) = 2 //装入物品2次
dp[3] = max(dp[3],dp[2] + 1) = max(0, 2 + 1) = 3 //装入物品3次

  上述过程对应的即是完全背包的求解过程
  因此，只要把01背包算法模板中的j改个遍历方向，改成从前向后遍历，就得到了完全背包的算法模板：

for (int i = 1; i <= n; i++) {
	for (int j = vi; j <= C; j++) {
		dp[j] = Math.max(dp[j], dp[j - vi] + wi);
	}
}

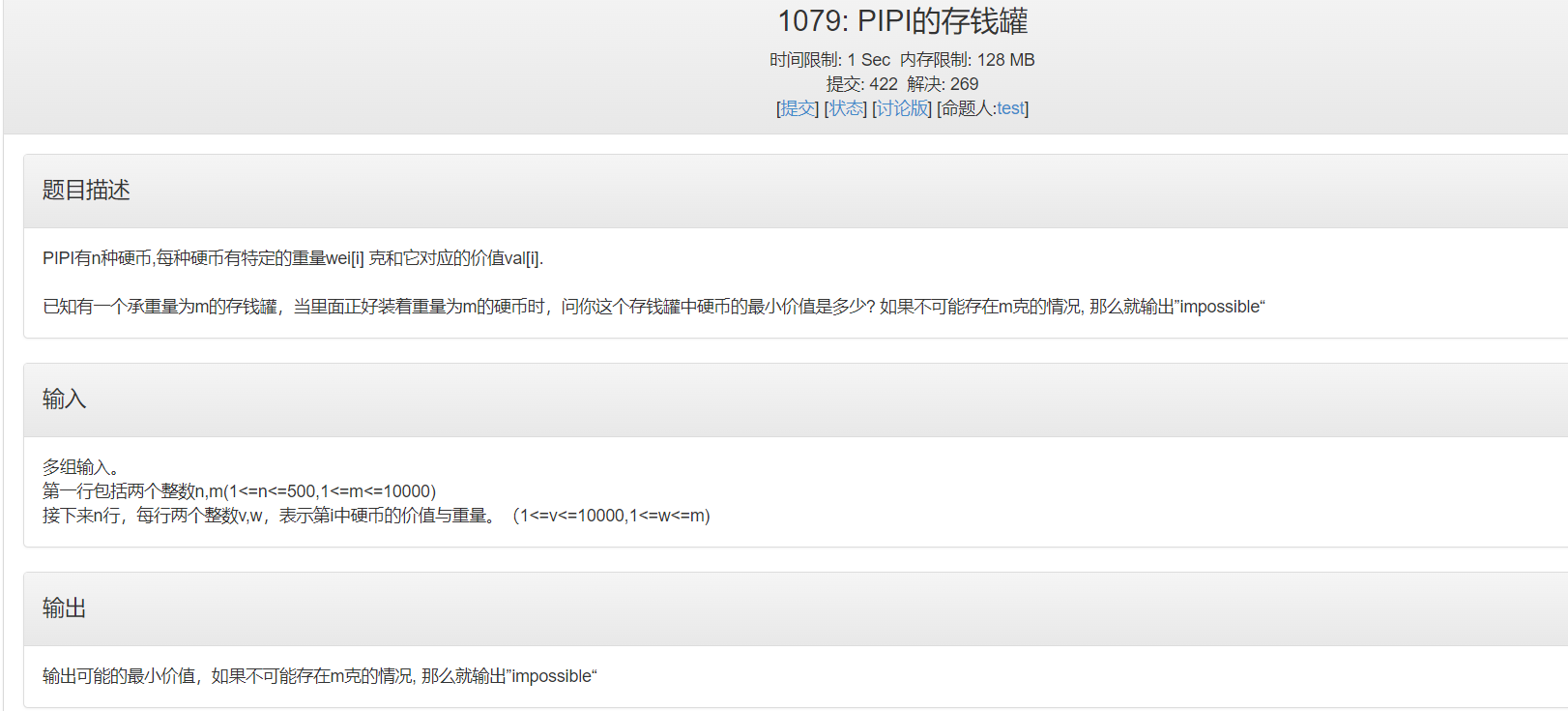
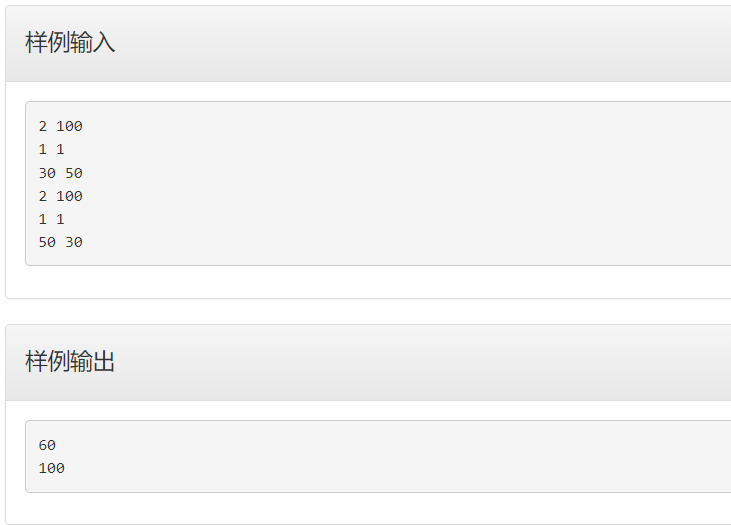
问题

思路

  该题为完全背包问题的板子题，唯一的区别在于是求最小价值和，那么我们将算法模板中的Math.max改为Math.min，使初始dp数组除dp[0] = 0外，其余都=INF，这样我们就可以求出最小价值和

代码

import java.util.*;

public class Main {
    static int[] dp = new int[10005];
    static int[] weight = new int[502];
    static int[] value = new int[502];
    static final int INF = 100000009;
    public static void main(String[] args) {
        int n, m, i, v, w, j, minV;
        Scanner scanner = new Scanner(System.in);
        while (scanner.hasNextInt()) {
            n = scanner.nextInt();
            m = scanner.nextInt();
            Arrays.fill(dp, INF);
            for (i = 0;i < n;i++) {
                v = scanner.nextInt();
                w = scanner.nextInt();
                weight[i] = w;
                value[i] = v;
            }
            dp[0] = 0;
            for (i = 0;i < n;i++) {
                for (j = weight[i]; j <= m; j++) {
                    dp[j] = Math.min(dp[j], dp[j - weight[i]] + value[i]);
                }
            }
            System.out.println(dp[m] == INF ? "impossible" : dp[m]);
        }
    }
}

最后

以上就是虚拟豌豆为你收集整理的DP + 完全背包问题：PIPI的存钱罐DP + 完全背包问题：PIPI的存钱罐的全部内容，希望文章能够帮你解决DP + 完全背包问题：PIPI的存钱罐DP + 完全背包问题：PIPI的存钱罐所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。