概述
本系列记录了我对随机微分方程的学习和理解，我将抛去严谨得有些繁复的数学证明和定义，试图用一个较为简单的思路去介绍一遍随机微分方程，如果希望获得详细的数学证明过程，请看各类数学教材，在本系列中不会涉及。
首先我们介绍布朗运动，这个随机过程在随机微分方程中占有重要的地位。回想初中我们对布朗运动的理解，是来源于那个“随意运动的花粉”：
布朗运动是指悬浮在液体或气体中的微粒所做的永不停息的无规则运动。其因由英国植物学家布朗所发现而得名。作布朗运动的微粒的直径一般为10-5~10-3厘米，这些小的微粒处于液体或气体中时，由于液体分子的热运动，微粒受到来自各个方向液体分子的碰撞，当受到不平衡的冲撞时而运动，由于这种不平衡的冲撞，微粒的运动不断地改变方向而使微粒出现不规则的运动。
布朗运动-百度百科
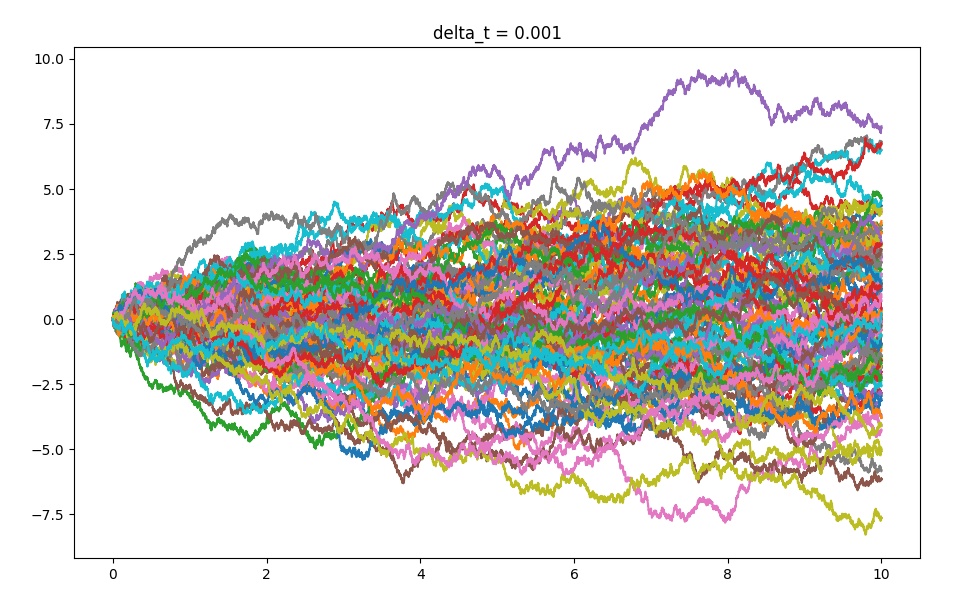
我们假设在时刻t，“花粉”的位置为
最后
以上就是轻松小土豆为你收集整理的levy过程和布朗运动的关系_随机微分方程入门（一）布朗运动与伊藤积分的引出...的全部内容，希望文章能够帮你解决levy过程和布朗运动的关系_随机微分方程入门（一）布朗运动与伊藤积分的引出...所遇到的程序开发问题。
如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。
本图文内容来源于网友提供，作为学习参考使用，或来自网络收集整理，版权属于原作者所有。
发表评论 取消回复