期权定价 - BS模型 - 维纳过程和伊藤引理

1. wiener Processes （维纳过程）

Stochastic processes(随机过程） ： Any variable whose value changes over time in an uncertain way is said to follow a stochastic process. Stochastic processes can be classified as discrete time or continuous time.

随机过程就是变量根据时间变化，而这个变化是不可预测的。随机过程分为离散时间和连续时间两种。

Markov Process(马尔科夫过程） ： a particular type of stochastic process whre only the current value of a variable is relevent for predicting the future.
马尔科夫过程是特殊的随机过程，只有当前变量值会影响后面的值，历史数据对后面的预测没有影响。拿到股票上面就是只有当前的股票价格对后续价格有影响，当前价格已经包含了历史数据的信息。
这符合weak form of market efficiency（弱式市场假说），如果历史数据可以预测后面的股价，那么很多人会据此获利，去购买某些预测会涨的股票，这些股票价格会飙升，破坏原有的pattern，达到一个新的平衡

股票价格波动量一般会符合正态分布，于是我们可以定义一个关于股票的马尔科夫过程，它的后续变动符合N(m,v)的正态分布， 其中m是均值，v是方差
例子：股票当前价格是10， 如果一年的变动符合N(0,1)，那么两年的变动则会符合N(0, 2)，均值是0，标准差是1和√2

Wiener Processes（维纳过程） ： It’s a particular type of Markov stochastic process with a mean change of zero and a variance rate of 1.0 per year.
维纳过程就是我们上述的一年变动符合N（0,1）的特殊马尔科夫过程

• 公式如下，Δz 是变动，ε符合标准正态分布N（0,1），√Δt是时间变动

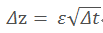
对于两个不同的Δt时间间隔，他们是无关的
于是有：
Δz 的均值是 0
Δz 的标准差是 √Δt
Δz 的方差是 Δt

于是Δz是符合马尔科夫过程的

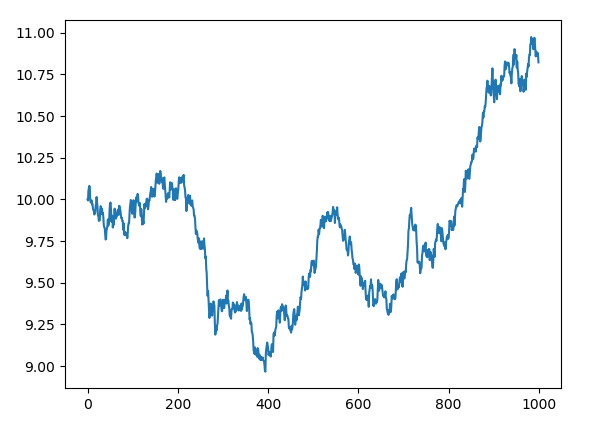
我们看一年的股票价格变动的话，应该是由每个Δt的变动加起来的，Δt取的越小出来的图应该就越细，但对于每个Δt都是跳跃的（jagged）。因为对于每个Δt，标准差是√Δt，Δt越小， √Δt会比Δt 大很多。
写个python程序验证一下维纳过程：

import numpy as np
import matplotlib.pyplot as plt
import math

daysCount = 1000
days = np.arange(0, daysCount, 1)
changes = np.random.randn(daysCount - 1, 1)*np.sqrt(1/daysCount)
prices = np.zeros(days.shape)

prices[0] = 10
for index in range(changes.shape[0]):
    prices[index + 1] = prices[index] + changes[index][0]

plt.plot(days, prices)
plt.show()

Generalized Wiener Process(广义维纳过程） ： The generalized Wiener Process has an expected drift rate of a and a variance rate of b2(平方）
广义维纳过程是维纳过程的扩充，为维纳过程增加了趋势项a，加上原来的维纳过程作为变量路径上的扰动。
我们之所以加入这个a，是因为股票投资者对于股票是有预期收益的，在风险中性的环境里这个预期收益应该等于无风险利率。
公式如下：

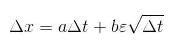
Δx 的均值是 aΔt
Δx 的标准差是 b√Δt
Δx 的方差是 b^2Δt

再画个图对比一下维纳过程a = 0.2， b=1.5：

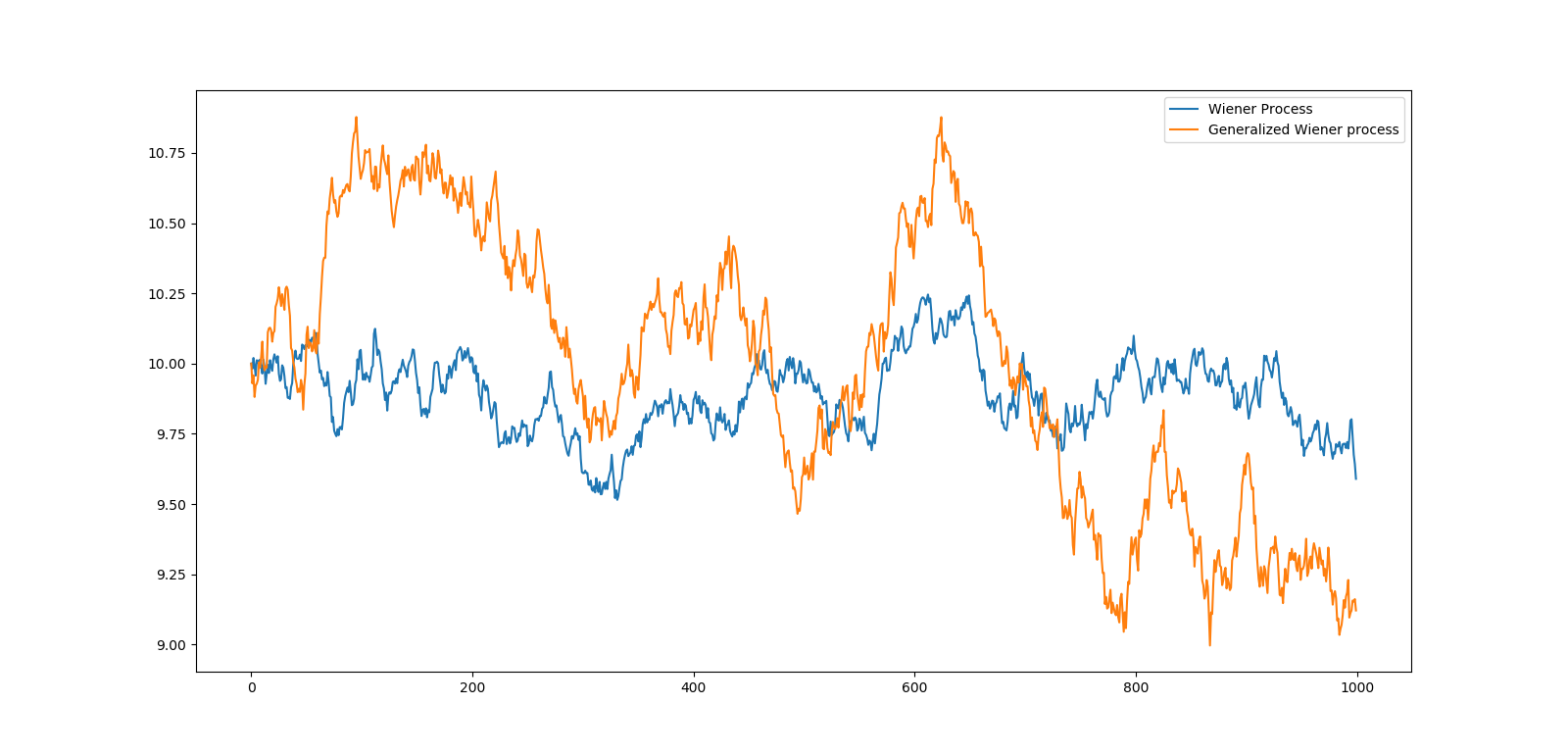
代码：

import numpy as np
import matplotlib.pyplot as plt
import math

#Wiener Process
daysCount = 1000
days = np.arange(0, daysCount, 1)
changes = np.random.randn(daysCount - 1, 1)*np.sqrt(1/daysCount)
prices = np.zeros(days.shape)

prices[0] = 10
for index in range(changes.shape[0]):
    prices[index + 1] = prices[index] + changes[index][0]

plt.plot(days, prices, label = "Wiener Process")

#Generalized Wiener Process
a = 0.3
b = 1.5
deltaT = 1/daysCount
changes_g = a*deltaT + np.random.randn(daysCount - 1, 1)*np.sqrt(1/daysCount) * b
prices_g = np.zeros(days.shape)
prices_g[0] = 10
for index in range(changes_g.shape[0]):
    prices_g[index + 1] = prices_g[index] + changes_g[index][0]

plt.plot(days, prices_g, label = 'Generalized Wiener process')
plt.legend()
plt.show()

2. Ito’s Lemma（伊藤引理）

Ito Process（伊藤过程） ： A further type of generalized Wiener process in which the parameters a and b are functions of the value of the underlying varaibles x and time t.
伊藤过程是维纳过程的扩充，让上面的a和b由常量变成了x和t的变量，公式如下：

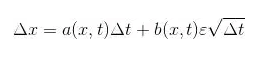
这里有个小的假设，a和b的值决定于时间t，并且在Δt时间内保持一致

The Process of Stock Price(股票价格过程）公式：
dS = μS dt + σS dz
dz = ε√Δt

考虑一支没有分红的股票，一年的volatility是30%，期望收益是15%一年，那么μ = 0.15，σ = 0.30
那么 dS = 0.15Sdt + 0.30Sdz

考虑一个礼拜，那么是0.0192 年，所以Δt = 0.0192.
则 dS = 0.15 * 0.0192 S + 0.30 * √0.0192 Sε

Ito’s Lemma(伊藤引理）
关于伊藤引理可以看这个链接，找了几个这个讲的最好：
https://zhuanlan.zhihu.com/p/38293827

股票价格过程是符合布朗运动的，但是布朗运动是处处不可微的，所以很难研究
dS = μS dt + σS dz
dz = ε√Δt

伊藤引理做了什么呢，他给出了公式证明把布朗运动函数作为变量的另外一个函数也是符合布朗运动的，而且这个函数G是处处可微的。
而金融衍生品的本质就是基于underlying的另外一个衍生品，可以用函数G来表达，于是我们可以研究了

伊藤引理带入股票价格过程的公式：

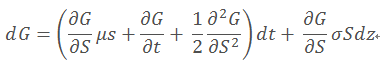
应用在forward contracts上面：

有一个远期合约，基于一个无分红的股票，无风险利率为r

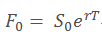
那么在时间t，t < T时的forward价格：

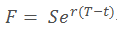
假设S的价格变化符合布朗运动：
dS = μS dt + σS dz
dz = ε√Δt

计算伊藤引理的参数：

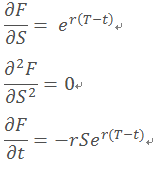
带入伊藤引理：

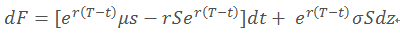
带入F：

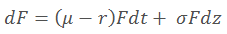
于是基于股票的衍生品还是符合布朗运动，但是变得可微了，也就是期权定价BS公式的基础

股票价格的对数正态分布
前面说了股票价格变动符合布朗运动：
dS = μS dt + σS dz
dz = ε√Δt

但是股票价格绝对值的变动不好衡量，比如从100涨到110和从1000涨到1100其实增幅是一样的，但如果直接用dS就是10和100的涨幅了，我们用比例比较好衡量，也就是都涨了10%，St/S0.
为了消除掉S的影响，我们把股票价格表示为G = ln（S）

带入前面伊藤引理的方程：

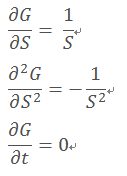
得到：

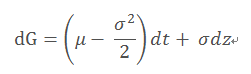
也就是说股票价格的对数变动符合上述的正态分布
均值：

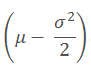
方差：

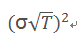
最后

以上就是单纯高山为你收集整理的期权定价 - BS模型 - 维纳过程和伊藤引理的全部内容，希望文章能够帮你解决期权定价 - BS模型 - 维纳过程和伊藤引理所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。