拉斯维加斯算法

65 阅读 0 评论 43 点赞

我是靠谱客的博主愉快钻石，最近开发中收集的这篇文章主要介绍拉斯维加斯算法，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

拉斯维加斯算法能显著改进算法的有效性，甚至为某些迄今为止找不到有效算法的问题，也能得到满意结果。
拉斯维加斯算法的一个显著特征是它所做的随机性策略可能找不到所需的解。典型的调用形式为bool success=LV(x,y)，其中x是输入参数，当success值为true时，y返回问题的解。当success值为false时，算法未能找到问题的解，此时可对同一实例再次独立地调用相同的算法。

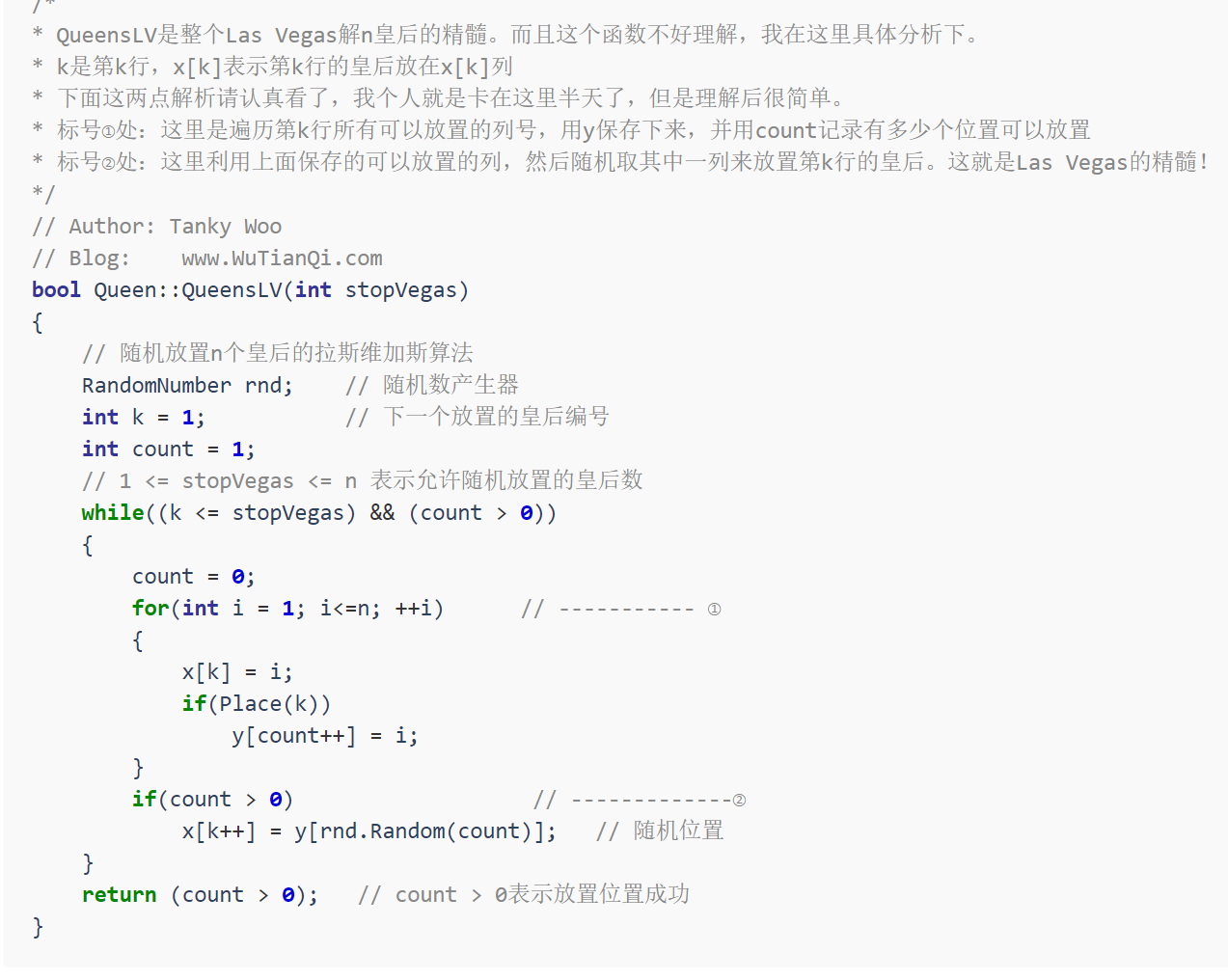
n后问题
在这里插入图片描述
整数n因子分割

具体过程如下：在开始时选取0～n-1范围内的随机数，然后递归地由
产生无穷序列对于i=2^{k，k=0,1,…以及2}k<j<=2^(k+1)，算法计算出xj-xi与n的最大公因子d=gcd(xj-xi，n)。如果d是n的非平凡因子，则实现对n的一次分割，算法输出n的因子d。

int gcd(int a,int b)     //辗转相除法求a与b的最大公约数 
{
	if(b==0) 
	   return 0;
	else 
	   return gcd(b,a%b);
}

void Pollard(int n)
{
	int i=1;
	int x=randomNum9(0,n-1);  //x为[0,n-1]之间的随机整数
	int k=2;
	y=x;
	while(true)
	{
		i++;
		x=(x*x-1)%n;  //Xi=[X(i-1)*X(i-1)-1]mod n
		d=gcd(y-x,n);
		if(d>1&&d<n)
		   return d;
		if(i==k)
		{
			y=x;
			k=k*2;
		} 
	} 
}