文章目录
- 一、进位计数制
- 1. 概念
- 2. 数字系统中的常用数制
- 二、进制转换
- 1. R进制转换成十进制
- 2. 十进制转换成R进制
- 3. 二进制与八进制、十六进制之间的转换
- 三、带符号二进制数的代码表示
- 1. 无符号二进制数
- 2. 有符号二进制数
- 四、几种常用的编码
- 一. 十进制数的二进制编码(BCD码)
- 1. 8421 码
- 2. 2421码
- 二、可靠性编码
- 1. 格雷 (Gray) 码
- 2. 奇偶校验码
- 三、字符编码
一、进位计数制
1. 概念
采用若干位 数码 进行计数,并规定 进位规则 的科学计数法称为 进位计数制 , 简称数制。数码的个数和计数规律是进位计数制的两个决定因素。
数制的要素:
- 数码 : 表示基本 数值大小 的不同 数字符号;基数:数码的个数;位权:每个位置上单位数码代表的数值。
- 进位规则 : 逢几进一,借一当几。
十进制数:
- 数码 : 0 , 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 0,1,2,3,4,5,6,7,8,9 0,1,2,3,4,5,6,7,8,9
- 基数 : 10 (数码的个数)
- 进位规则 :逢十进一,借一当十
- 位权 :每个位置代表的数值大小, 1 0 i 10^i 10i。

其中:
n
n
n 为整数位数,
m
m
m 为小数位数
a
i
a_i
ai 为 为
0
,
1
,
…
,
9
0, 1, … , 9
0,1,…,9
e . g . e.g. e.g. ( 563.48 ) 10 = 5 × 1 0 2 + 6 × 1 0 1 + 3 × 1 0 0 + 4 × 1 0 − 1 + 8 × 1 0 − 2 (563.48)_{10}=5 ×10^2+ 6 ×10^1+3 ×10^0+4 ×10^{-1} +8 ×10^{-2} (563.48)10=5×102+6×101+3×100+4×10−1+8×10−2
2. 数字系统中的常用数制
二进制;八进制;十六进制。
数字系统内的数是以器件的 物理状态 来表示的,二进制数只需要 两种不同状态 即可表示, 因此数字系统采用二进制数。
书写时, 二进制数往往很长;为了书写方便,常采用八进制或十六进制数。
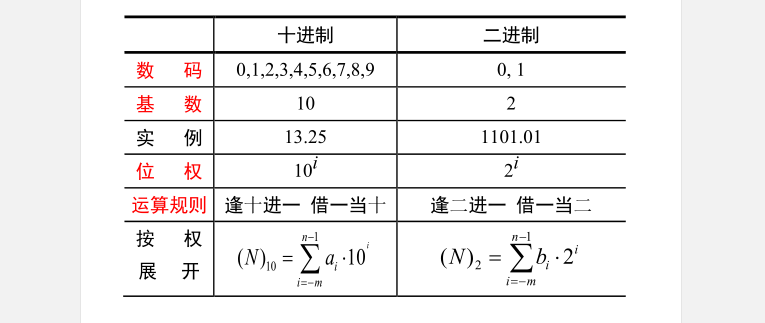
二进制的规则如下:

八进制的规则如下:
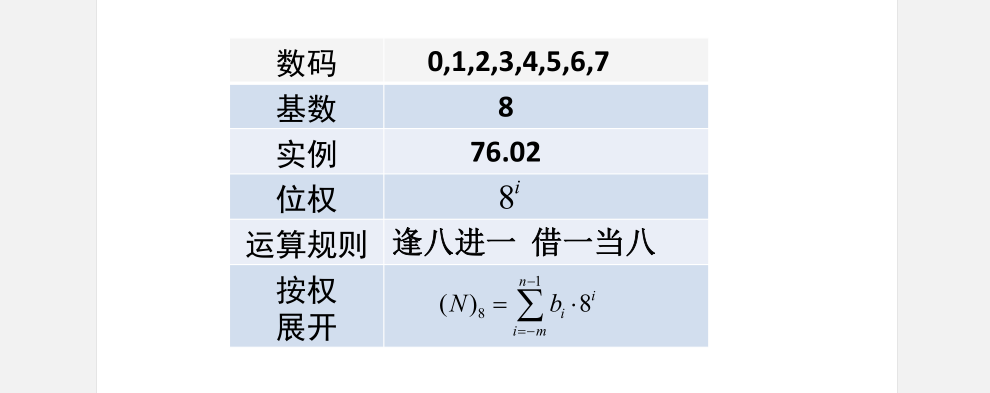 十六进制规则如下:
十六进制规则如下:

二、进制转换
1. R进制转换成十进制
- 数码: 基本符号 0 , 1 , 2 , . . . , ( R − 1 ) 0,1,2, ..., (R-1) 0,1,2,...,(R−1)
- 基数: R R R
- 位权: R i R_i Ri
- 运算规则 :逢 R R R进一 , 借一当 R R R。
将 R R R 进制数 按位权展开, 再按十进制进行计算, 即得到对应的十进制数。
e . g . e.g. e.g.
- ( 53.62 ) 7 = 5 × 7 1 + 3 × 7 0 + 6 × 7 − 1 + 2 × 7 − 2 = ( 38.898 ) 10 ( 53.62)_7 = 5 ×7^1+3 ×7^0 +6 ×7^{-1}+2 ×7^{-2} = ( 38.898 )_{10} (53.62)7=5×71+3×70+6×7−1+2×7−2=(38.898)10
- ( 24.3 ) 5 = 2 × 5 1 + 4 × 5 0 + 3 × 5 − 1 = ( 14.6 ) 10 ( 24.3 )_5= 2 ×5^1+4 ×5^0+3 ×5^{-1}= ( 14.6 )^{10} (24.3)5=2×51+4×50+3×5−1=(14.6)10
2. 十进制转换成R进制
整数部分:连续除基取余倒排法,商零为止。
e
.
g
.
e.g.
e.g.
(
25
)
10
=
(
11001
)
2
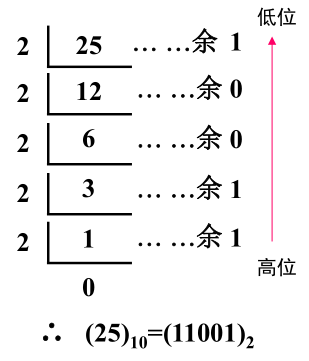
(25)_{10} = (1 1001)_2
(25)10=(11001)2,过程如下:
e
.
g
.
e.g.
e.g.
(
54
)
10
=
(
36
)
16
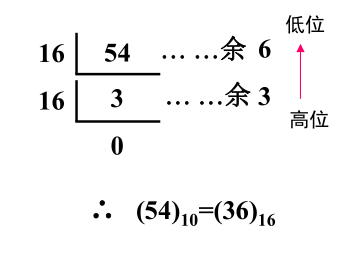
(54)_{10} = (36)_{16}
(54)10=(36)16,过程如下:
小数部分:连续乘基取整正排法:乘基取整 , 直至满足精度要求或乘积小数部分为
0
0
0。
e . g . e.g. e.g. ( 0.93 ) 10 = ( 0.11101 ) 2 (0.93)_{10} = (0.11101)_2 (0.93)10=(0.11101)2
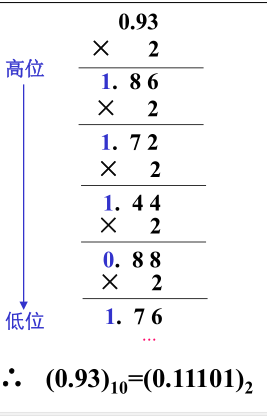 总结:
总结:
整数部分转换: 除以基数R 取余数
- 整数部分除以基数R, 余数作为等值的R进制数最低位;
- 将商再除以R,余数作为等值的R进制数的次低位;
- 重复步骤2,直到商等于零为止。
小数部分转换: 乘以基数R 取整数
- 小数部分乘以基数R,积的整数部分为R进制数的最高位;
- 将小数部分再乘以基数R,其积的整数部分为次高位;
- 重复步骤2,直到达到要求的精度为止。
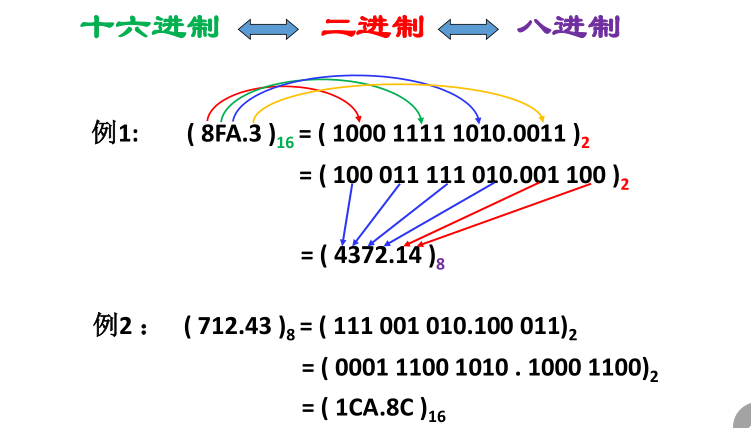
3. 二进制与八进制、十六进制之间的转换
这个转换特别一点,不是很麻烦的通过十进制进行转换,而是直接写:
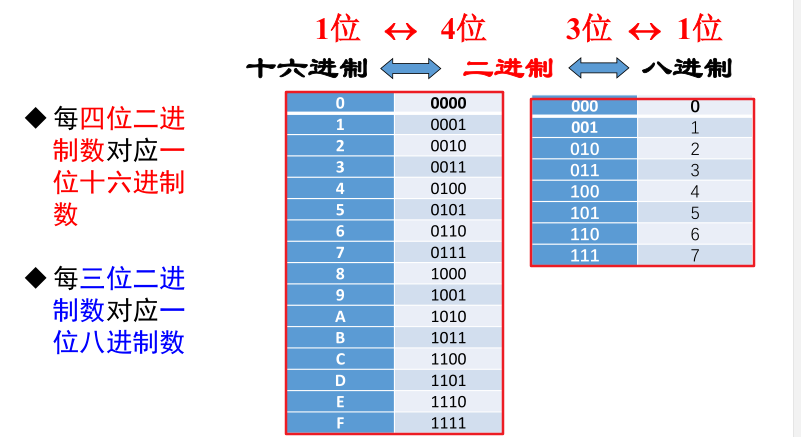
十六进制转换成二进制:

二进制转换为十六进制:
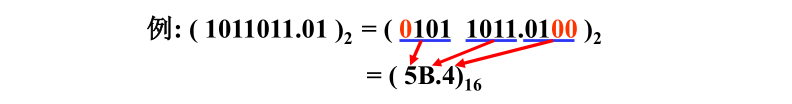
二进制转换为八进制数: 从小数点起每三位分一组,不足三位补零。
e
.
g
.
e.g.
e.g.
(
11010101.01011
)
2
=
(
011
010
101
.
010
110
)
2
=
(
325.26
)
8
( 11010101.01011)_2 = ( 011 010 101 . 010 110)_2 = ( 325.26 )_8
(11010101.01011)2=(011 010 101 . 010 110)2=(325.26)8
e
.
g
.
e.g.
e.g.
(
111001010.100101
)
2
=
(
111
001
010
.
100
101
)
2
=
(
712.45
)
8
( 111001010.100101)_2 = (111 001 010 . 100 101)_2 = ( 712.45 )_8
(111001010.100101)2=(111 001 010 . 100 101)2=(712.45)8
八进制数转换为二进制数:将每一位八进制数位表示成三位二进制数。
e
.
g
.
e.g.
e.g.
(
325.26
)
8
=
(
011
010
101
.
010
110
)
2
=
(
11010101.01011
)
2
( 325.26 )_8 = ( 011 010 101 . 010 110)_2 = ( 11010101.01011)_2
(325.26)8=(011 010 101 . 010 110)2=(11010101.01011)2
e
.
g
.
e.g.
e.g.
(
712.45
)
8
=
(
111
001
010
.
100
101
)
2
( 712.45 )_8 = ( 111 001 010 . 100 101)_2
(712.45)8=(111 001 010 . 100 101)2
从这里可以看出,八进制和十六进制不是计算机中真实使用的进制,它的目的在于缩减二进制数的长度,方便给人看。
三、带符号二进制数的代码表示
1. 无符号二进制数
特点:无符号位。 A n − 1 A n − 2 . . . A 1 A 0 A_{n-1}A_{n-2}...A_1A_0 An−1An−2...A1A0表示范围 [ 0 , 2 n − 1 ] [0, 2^{n}-1] [0,2n−1]。
2. 有符号二进制数

原码:最高位为符号位,
0
0
0 表示 正数,
1
1
1 表示 负数,数值位就是自然二级制码。
- 正数 [+18]原 = 0 10010
- 负数 [- 18]原 = 1 10010
- [+0]原 = 0 0000000
- [- 0]原 = 1 0000000
- [+1]原 = 0 0000001
- [- 0]原 = 1 0000001
- [+127]原 = 0 1111111
- [- 127]原 = 1 1111111
反码 :正数的反码与原码相同,符号位为0;负数的反码为 原码按位取反 ( 数值部分),符号位为1。
-
正数 [+18]反 = 0 10010
-
负数 [- 18]反 = 1 01101
-
[+0]反 = 0 0000000
-
[- 0]反= 1 1111111
-
[+1]反 = 0 0000001 [- 1] 反
= 1 1111110
[+127] 反 = 0 1111111 [- 127] 反 = 1 0000000
补码 :正数的补码与原码相同;负数的补码为 反码+1 ( 数值部分),符号位为1。 -
正数 [+18]补 = 0 10010
-
负数 [- 18]补 = 1 01110
四、几种常用的编码
一. 十进制数的二进制编码(BCD码)
用 4 4 4 位二进制代码对十进制数字符号进行编码 , 简称为二 – 十进制代码 , 或称 B C D ( B i n a r y C o d e d D e c i m a l ) BCD(Binary Coded Decimal) BCD(Binary Coded Decimal) 码。
根据代码中每一位是否有固定的权 , 通常将 BCD 码分为有权码 和 无权码 两种类型 。BCD 码既有二进制的形式, 又有十进制的特点 。 常用的 BCD 码有 8421 码、 2421 码和 余3码 。
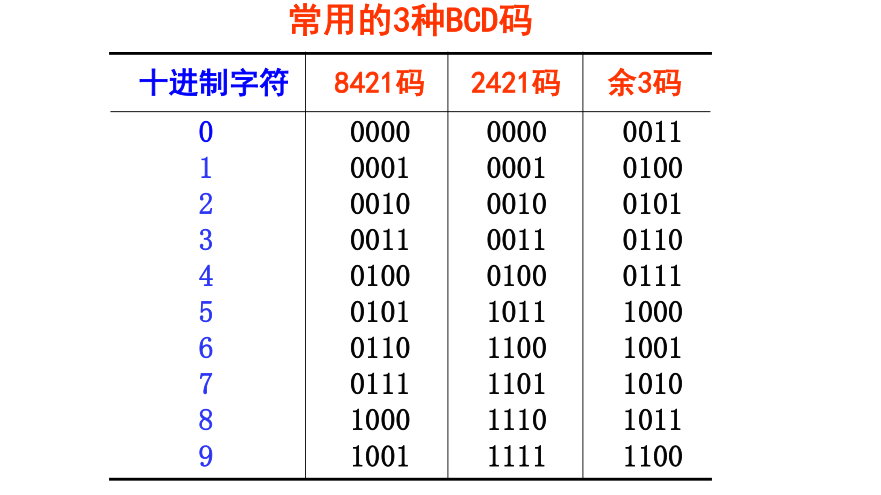
1. 8421 码
用 4 位二进制码 表示 一 位十进制字符的一种有权码,4 位二进制码从高位至低位的权依次为 2 3 2^3 23、 2 2 2^2 22 、 2 1 2^1 21 、 2 0 2^0 20 , 故称为 8421 码。8421 码中不允许出现 1010 ~ 1111 六 种组合 ( 因为没有十进制数字符号与其对应) 。
8421 码与十进制数之间的转换 ≠ neq = 二进制数和十进制数的转换,8421码与十进制数之间的转换是按位进行的 , 即十进制数的每一位与4 位二进制编码对应 。
e
.
g
.
e.g.
e.g.
(
258
)
10
=
(
0010
0101
1000
)
8421
码
(258)_{10} = (0010 0101 1000)_{8421 码}
(258)10=(0010 0101 1000)8421码
e
.
g
.
e.g.
e.g.
(
28
)
10
=
(
1
1100
)
2
=
(
0010
1000
)
8421
码
(28)_{10} = (1 1100 )_2 = (0010 1000)_{8421 码}
(28)10=(1 1100)2=(0010 1000)8421码
2. 2421码
是用 4 位二进制码 表示 一 位十进制字符的一种有权码 ,4 位二进制码从高位至低位的权依次为2,4,2,1, 故称为 2421 码 。若 一个十进制字符 X X X 的 2421 码为 a 3 a 2 a 1 a 0 a_3 a_2a_1a_0 a3a2a1a0 , 则该字符的 值为: X = 2 a 3 + 4 a 2 + 2 a 1 + 1 a 0 X = 2a_3 + 4a_2 + 2a_1 +1 a_0 X=2a3+4a2+2a1+1a0
2421 码与十进制数之间的转换同样是按位进行的 , 例如:
e
.
g
.
e.g.
e.g.
(
258
)
10
=
(
0010
1011
1110
)
2421
码
( 258)_{10} = (0010 1011 1110)_{2421 码}
(258)10=(0010 1011 1110)2421码
e
.
g
.
e.g.
e.g.
(
0010
0001
1110
1011
)
2421
码
=
(
2185
)
10
(0010 0001 1110 1011)_{2421 码} = (2185)_{10}
(0010 0001 1110 1011)2421码=(2185)10
(1) 2421码不具备单值性 。 例如, 0101 和 1011 都对应十进制数字5。 为了与十进制字符一一对应 , 2421 码不允许出现
0101 ~ 1010的 6 种状态 。
(2) 2421码是一种对9的自补代码 。 即一个数的 2421 码只要自身按位变反,便可得到该数对9的补数的 2421 码 。具有 这一特征的 BCD 码可给运算带来方便 , 因为直接对 BCD 码进行运算时 , 可利用其对9 的补数将减法运算转化为加法运算。
e . g . e.g. e.g. ( 4 ) 10 = ( 0100 ) 2421 = > ( 1011 ) 2421 = ( 5 ) 10 (4)_{10} = (0100)_{2421} => (1011)_{2421} =(5)_{10} (4)10=(0100)2421=>(1011)2421=(5)10
二、可靠性编码
作用: 减少 或者 发现 代码在形成和传送过程中可能发生的错误,提高系统的可靠性。
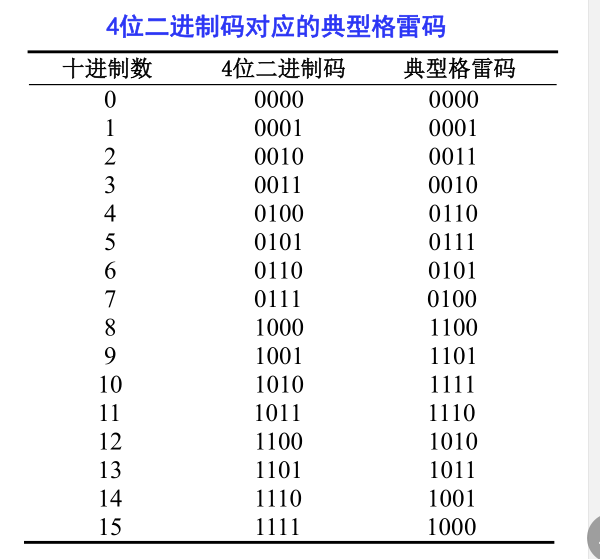
1. 格雷 (Gray) 码
特点: 任意两个相邻的数, 其格雷码仅有一位不同。
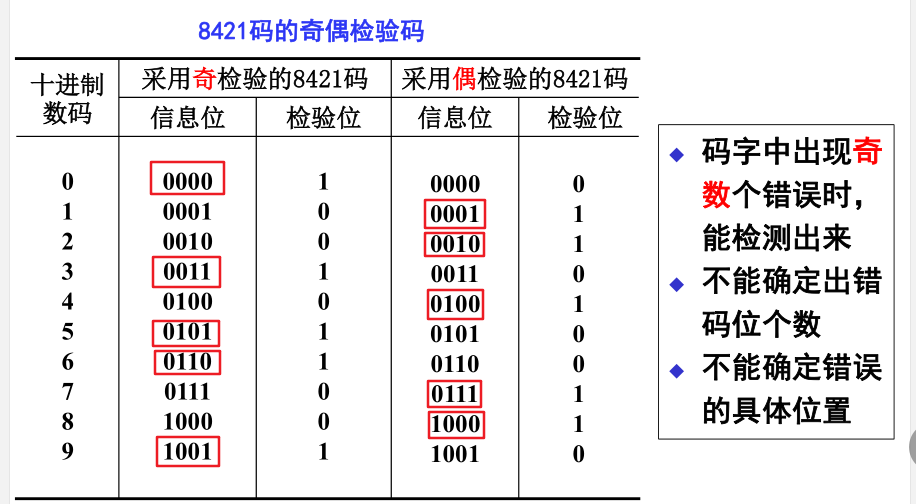
2. 奇偶校验码
是 一种用来检验代码在传送过程中是否产生错误的代码。
(1) 组成:
信息位——位数不限的一组二进制代码
奇偶检验位——仅有一位
(2) 编码 方式:有两种编码 方式
奇 检验: 使信息位和检验位中
1
1
1 的个数共计为奇数 ;
偶 检验: 使信息位和检验位中
1
1
1 的个数共计为偶数 。

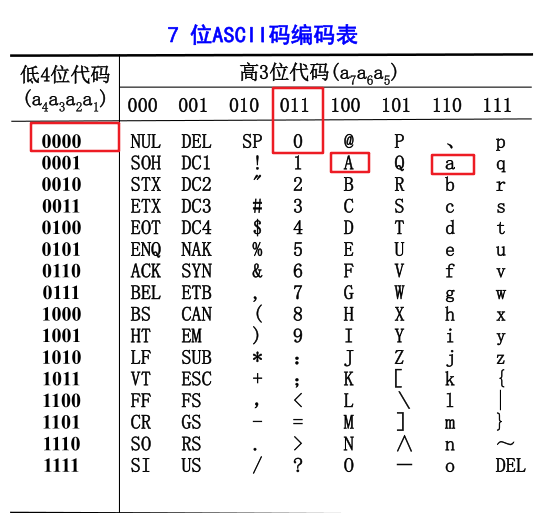
三、字符编码
ASCII码(美国信息交换标准码)用 7 位二进制数编码 128 个字符, 包括大 、小写字母, 数字 0 到 9,标点符号, 以及在美式英语中使用的特殊控制字符等。
最后
以上就是娇气日记本最近收集整理的关于【数字逻辑】学习笔记 第二章 数制和编码的全部内容,更多相关【数字逻辑】学习笔记内容请搜索靠谱客的其他文章。








发表评论 取消回复