多因素蚁群算法的移动机器人路径规划研究（Matlab代码实现）

89 阅读 0 评论 59 点赞

我是靠谱客的博主诚心朋友，最近开发中收集的这篇文章主要介绍多因素蚁群算法的移动机器人路径规划研究（Matlab代码实现），觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

????????????????????????欢迎来到本博客❤️❤️❤️????????????

????博主优势：????????????博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

目录

????1 文献阅读

????2 概述

????3 运行结果

????‍????4 Matlab代码实现

????1 文献阅读

????2 概述

以上改进算法大多致力于提高蚁群算法的搜索效率,得到尽可能短的路径,但并没有在路径的其他最优因素上进行研究。本文在前人的研究基础上，提出一种多因素的蚁群算法,利用路程长度、转弯次数以及坡度大小三种启发信息,使蚂蚁以多类型信息为基础寻找合适栅格，使搜索的路径在综合多种因素的基础上表现最优,并且结合多因素的信息素更新模型,综合评价各可行路径的优劣,并分配信息素,再结合改进的栅格地图建模法,利用非均匀初始信息素加快算法的收敛,可以得到较好的结果。

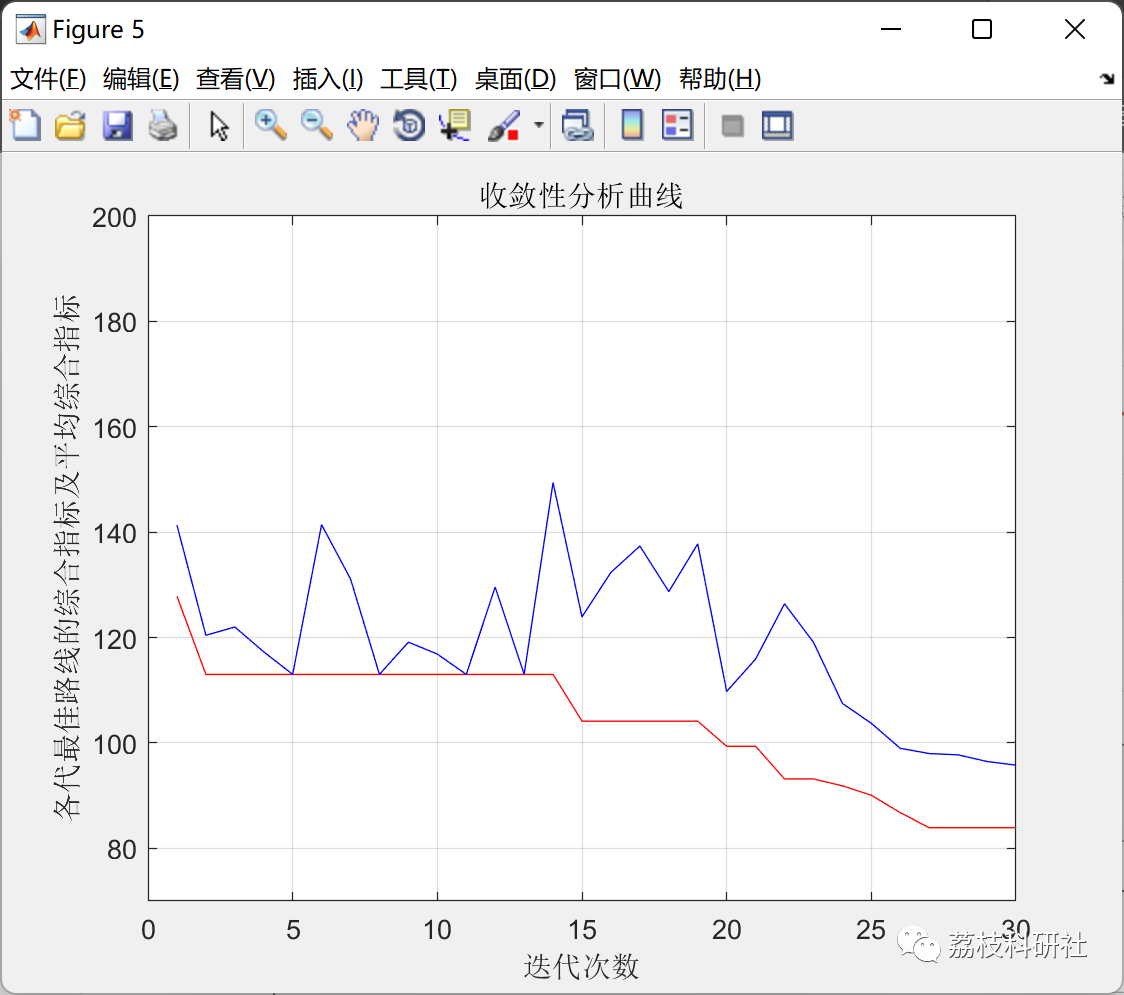
????3 运行结果

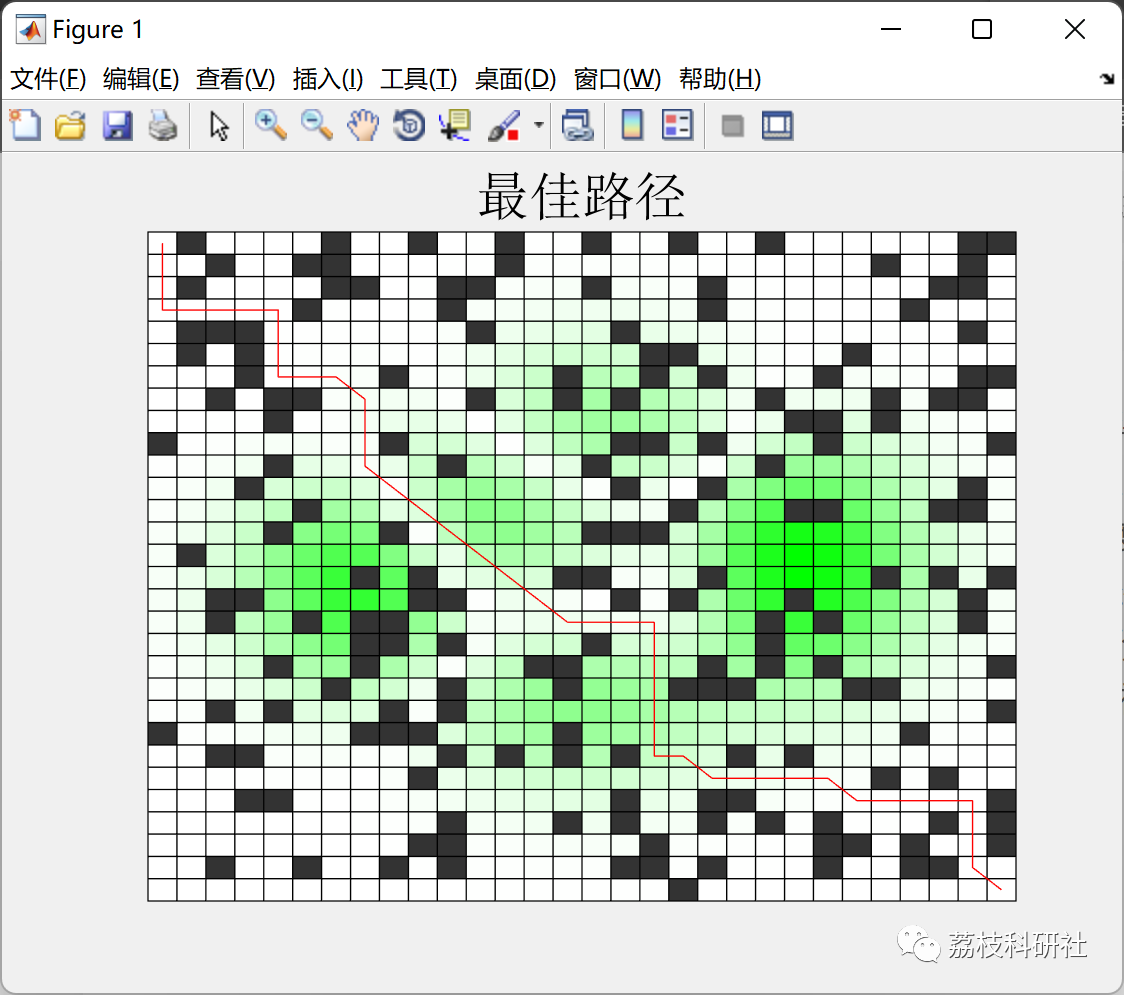
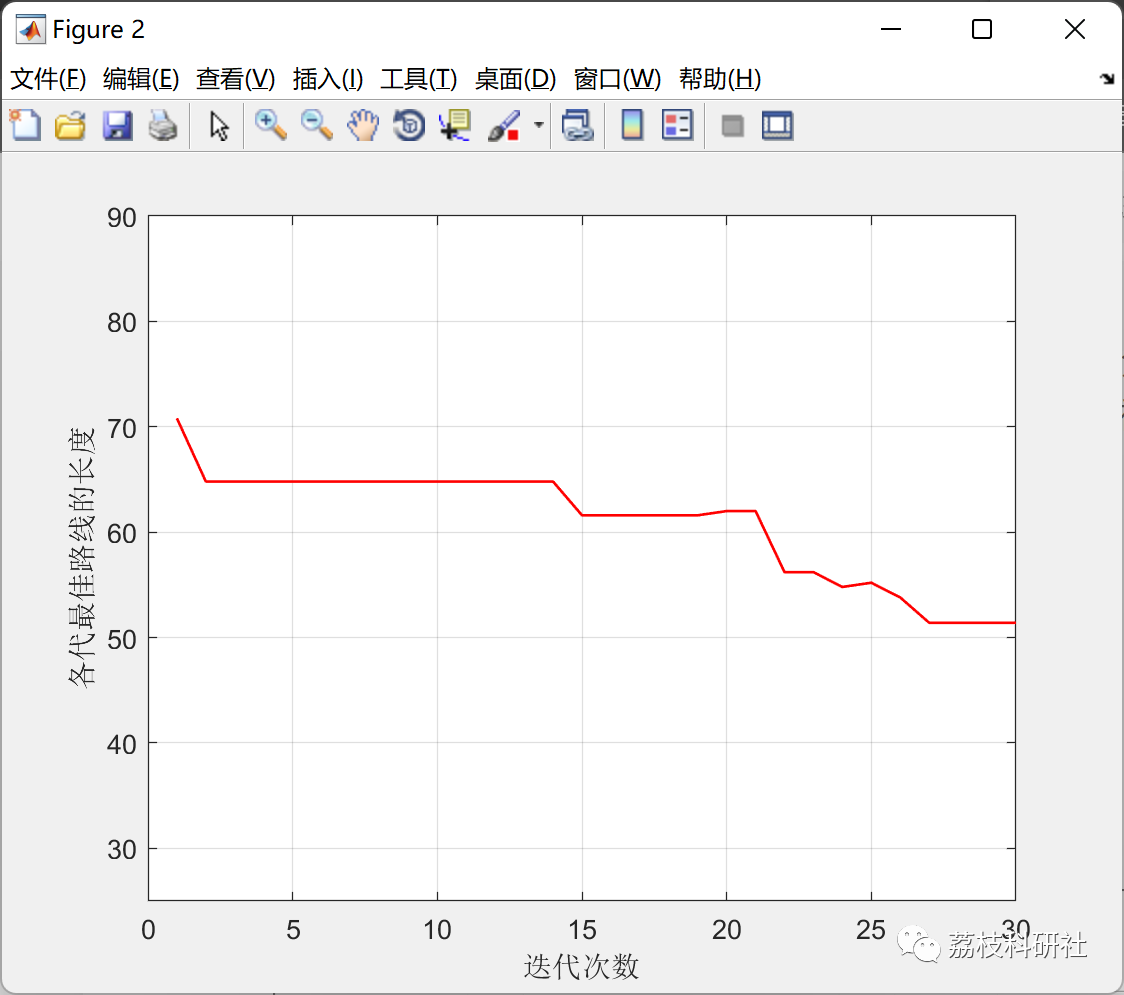
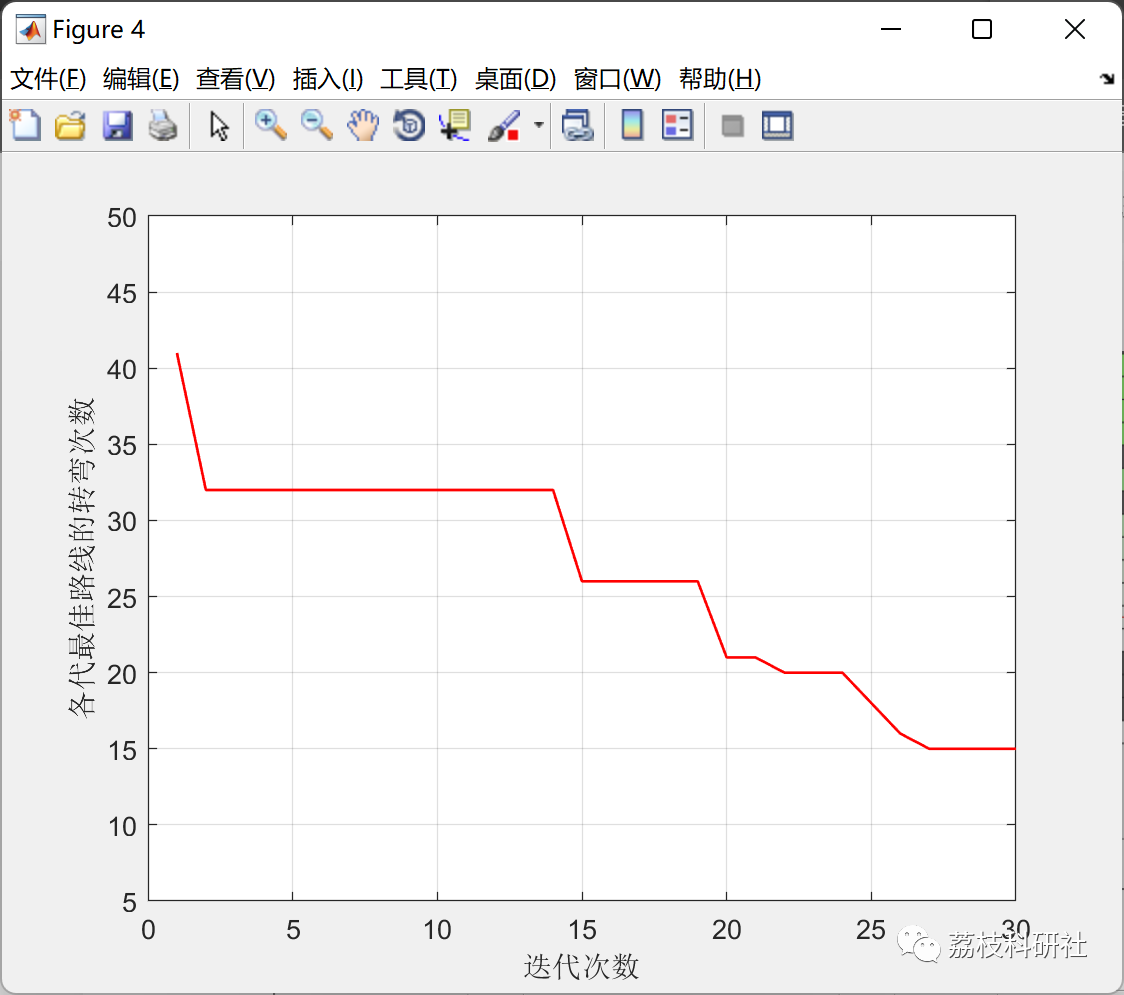
部分代码：

%% 第一步：变量初始化
global MM;
global Lgrid;
global Dir;
Tau=20*ones(MM^2,8); %Tau为信息素矩阵
NC=1; %迭代计数器
R_best=zeros(NC_max,MM^2); %各代最佳路线(行数为最大迭代次数NC_max，列数为走过栅格数量)
R_best_to_direct=zeros(NC_max,MM^2); %各代最佳路线（转移方向）
L_best=inf.*ones(NC_max,1); %各代最佳路线的长度（inf:无穷大）
F_best=zeros(NC_max,1); %各代最佳路线高度均方差
T_best=zeros(NC_max,1); %各代最佳路线转弯次数
S_best=zeros(NC_max,1); %各代最佳路线综合得分
S_ave=zeros(NC_max,1); %各代路线的平均长度
inum = MM+(initial(1)/Lgrid-0.5)*MM-(initial(2)/Lgrid-0.5); %初始坐标转换为栅格标号
dnum = MM+(destination(1)/Lgrid-0.5)*MM-(destination(2)/Lgrid-0.5); %终点坐标转换为栅格标号
Tabu=zeros(m,MM^2); %存储并记录路径的生成tabu:（停止，禁忌表）（m行矩阵）
to_direct=zeros(m,MM^2); %存储并记录路径的转移方向过程（m行矩阵）
while NC<=NC_max %停止条件之一：达到最大迭代次数
%% 第二步：m只蚂蚁按概率函数选择下一栅格
%{
if NC<c
Alpha = 4*NC/c;
Beta = (3*c-1.5*NC)/c;
else
%}
Alpha = 1;
Beta = 3;
%end

Tabu(:,1)=inum; %将初始栅格加入禁忌表
for i=1:m
j=2; %栅格从第二个开始
while Tabu(i,j-1)~=dnum
visited=Tabu(i,1:(j-1)); %已访问的栅格
J=zeros(1,1); %待访问的栅格
N=J; %待访问的栅格转移方向
P=J; %转移概率分布
Jc=1; %循环下标
for k=1:8 %利用循环求解待访问的栅格，如果第k个栅格不属于已访问的栅格，则其为待访问的栅格
k1 = Dir(k)+visited(end);
if D(visited(end),k)==inf
continue
end
if isempty(find(visited==k1, 1)) % if length(find(visited==k))==0
J(Jc)=k1;% 含待访问栅格标号矩阵
N(Jc)=k; % 含待访问栅格转移标号矩阵
Jc=Jc+1; %下标加1，便于下一步存储待访问的栅格
end
end
if J==0 %死路的情况
Tabu(i,:)=0;
to_direct(i,:)=0;
break
end
max_dis = max(dis(J));
delta_dis = max(dis(J))-min(dis(J))+0.001;
max_h=max(abs(h(visited(end))-h(J)));
delta_v=max(h(visited(end))-h(J))-min(h(visited(end))-h(J))+0.001;
%计算待访问栅格的转移概率分布和启发式信息概率分布
for k=1:length(J) %sum(J>0)表示待访问的栅格的个数
if j==2
r = u/length(J);
elseif N(k)==to_direct(i,j-2)
r = 0.5*u;
else
r = 0.5*u/length(J);
end
Phi=(max_dis-dis(J(k)))/delta_dis*Omega+Mu;
d=D(visited(end),N(k));
v=(max_h-abs(h(visited(end))-h(J(k))))/delta_v*Omega+Mu;
Eta=r+1/d+Phi+v;
P(k)=Tau(visited(end),N(k))^Alpha*Eta^Beta; %概率计算公式中的分子
end %Tau为信息素矩阵,Eta为启发因子矩阵
P=P/(sum(P)); %转移概率分布：长度为待访问栅格个数
%按概率原则选取下一个栅格
Pcum=cumsum(P); %cumsum求累加和: cumsum([1 1 1])= 1 2 3，求累加的目的在于使Pcum的值总有大于rand的数
Select=find(Pcum>=rand); %当累积概率和大于给定的随机数，则选择个被加上的最后一个栅格作为即将访问的栅格
Tabu(i,j)=J(Select(1)); %将访问过的栅格加入禁忌表中
to_direct(i,j-1) = N(Select(1)); %to_direct表示即将访问的栅格转移方向
j=j+1;
end

end

if NC>=2 %如果迭代次数大于等于2，则将上一次迭代的最佳路线存入Tabu的第一行中
Tabu(1,:)=R_best(NC-1,:);
to_direct(1,:)=R_best_to_direct(NC-1,:);
end
%% 第三步：记录本次迭代最佳路线
L=zeros(m,1);
F=zeros(m,1);
T=zeros(m,1);
S=zeros(m,1);
x=1;y=100;z=1;
for i=1:m
if Tabu(i,:)==0 %去掉死路的情况
L(i)=inf;
F(i)=inf;
T(i)=inf;
S(i)=inf;
continue
end
F(i)=std(h(Tabu(i,:)~=0)); %求走过路径的高度的均方差
j=2;
L(i)=Lgrid*D(Tabu(i,1),to_direct(i,1));
while Tabu(i,j+1)~=0
L(i)=L(i)+Lgrid*D(Tabu(i,j),to_direct(i,j)); %求路径距离
T(i)=T(i)+~(~(to_direct(i,j)-to_direct(i,j-1))); %求转弯的次数
j=j+1;
end
S(i)=x*L(i)+y*F(i)+z*T(i); %求综合路径评分
end
S_best(NC)=min(S); %最优路径为综合最优的路径
if S_best(NC)==inf
error('没有通路');
end
pos=find(S==S_best(NC)); %找出最优路径对应的位置：即是哪只个蚂蚁
R_best(NC,:)=Tabu(pos(1),:); %确定最优路径对应的栅格顺序
R_best_to_direct(NC,:)=to_direct(pos(1),:); %确定最优路径对应的栅格转移方向顺序
L_best(NC) = L(pos(1)); %各代最优路线长度
F_best(NC) = F(pos(1)); %各代最优路线高度均方差
T_best(NC) = T(pos(1)); %各代最优路线转弯次数
S_ave(NC)=mean(S(S~=inf)); %求第k次迭代的平均综合指标(去掉死路的情况)
NC=NC+1;
%% 第四步：更新信息素
%n = sum((to_direct(pos(1),:)~=0));
Delta_Tau=zeros(MM^2,8); %Delta_Tau（i,j）表示所有的蚂蚁留在第i个栅格到相邻8个栅格路径上的信息素增量
for i=1:m
for j=1:MM^2 %建立了完整路径后路径后在释放信息素：Q/S(i)
if Tabu(i,j)==0||Tabu(i,j+1)==0 %排除死路蚂蚁情况
break
else
Delta_Tau(Tabu(i,j),to_direct(i,j))=Delta_Tau(Tabu(i,j),to_direct(i,j))+Q/S(i);
end
end
end
if Tau<Tau_min %有界的信息素
Tau=Tau_min;
elseif Tau>Tau_max
Tau=Tau_max;
end
Tau=(1-Rho).*Tau+Delta_Tau; %信息素更新公式
if 0.95*Rho>Rho_min %有界的动态挥发系数
Rho=0.95*Rho;
else
Rho=Rho_min;
end
%% 第五步：禁忌表清零
Tabu=zeros(m,MM^2); %每迭代一次都将禁忌表清零
to_direct=zeros(m,MM^2); %转移方向矩阵清零
end
%% 第六步：输出结果
Pos=find(S_best==min(S_best)); %找到L_best中最小值所在的位置并赋给Pos
Shortest_Route=R_best(Pos(1),:); %提取最短路径
Shortest_Route=Shortest_Route(Shortest_Route~=0);%去掉全是死路的情况
Shortest_Length=L_best(Pos(1)); %提取最短路径的长度
end